460 lines
33 KiB
Markdown
460 lines
33 KiB
Markdown
# 不确定性问题
|
||
|
||
- 上一讲中,我们讨论了人工智能如何表示和推导新知识。然而,在现实中,人工智能往往对世界只有部分了解,这给不确定性留下了空间。尽管如此,我们还是希望我们的人工智能在这些情况下做出尽可能好的决定。例如,在预测天气时,人工智能掌握了今天的天气信息,但无法 100% 准确地预测明天的天气。尽管如此,我们可以做得比偶然更好,今天的讲座是关于我们如何创造人工智能,在有限的信息和不确定性的情况下做出最佳决策。
|
||
|
||
## 概率 (Probability)
|
||
|
||
- 不确定性可以表示为多个事件以及每一个事件发生的可能性或概率。
|
||
|
||
### 概率世界
|
||
|
||
- 每一种可能的情况都可以被视为一个世界,由小写的希腊字母$ω$表示。例如,掷骰子可以产生六个可能的世界:骰子出现 1 的世界,骰子出现 2 的世界,依此类推。为了表示某个世界的概率,我们写$P(ω)$。
|
||
|
||
### 概率公理
|
||
|
||
- $0<P(ω)<1$ :表示概率的每个值必须在 0 和 1 之间。
|
||
- 0 是一个不可能发生的事件,就像掷一个标准骰子并出现 7 一样。
|
||
- 1 是肯定会发生的事件,比如掷标准骰子,得到的值小于 10。
|
||
- 一般来说,值越高,事件发生的可能性就越大。
|
||
- 每一个可能发生的事件的概率加在一起等于 1。
|
||
|
||
$
|
||
\sum_{\omega\in\Omega}P(\omega)=1
|
||
$
|
||
|
||
- 用标准骰子掷出数字 R 的概率可以表示为 $P(R)$ 。在我们的例子中,$P(R)=1/6$ ,因为有六个可能的世界(从 1 到 6 的任何数字),并且每个世界有相同的可能性发生。现在,考虑掷两个骰子的事件。现在,有 36 个可能的事件,同样有相同的可能性发生。
|
||
|
||

|
||
|
||
- 然而,如果我们试图预测两个骰子的总和,会发生什么?在这种情况下,我们只有 11 个可能的值(总和必须在 2 到 12 之间),而且它们的出现频率并不相同。
|
||
|
||

|
||
|
||
- 为了得到事件发生的概率,我们将事件发生的世界数量除以可能发生的世界总数。例如,当掷两个骰子时,有 36 个可能的世界。只有在其中一个世界中,当两个骰子都得到 6 时,我们才能得到 12 的总和。因此,$P(12)=\frac{1}{36}$,或者,换句话说,掷两个骰子并得到两个和为 12 的数字的概率是$\frac{1}{36}$。$P(7)$是多少?我们数了数,发现和 7 出现在 6 个世界中。因此,$P(7)=\frac{6}{36}=\frac{1}{6}$。
|
||
|
||
### 无条件概率 (Unconditional Probability)
|
||
|
||
- 无条件概率是指在没有任何其他证据的情况下对命题发生的概率。到目前为止,我们所问的所有问题都是无条件概率的问题,因为掷骰子的结果并不取决于之前的事件。
|
||
|
||
## 条件概率 (Conditional Probability)
|
||
|
||
- 条件概率是在给定一些已经揭示的证据的情况下,命题发生的概率。正如引言中所讨论的,人工智能可以利用部分信息对未来进行有根据的猜测。为了使用这些影响事件在未来发生概率的信息,我们需要依赖条件概率。
|
||
- 条件概率用以下符号表示:$P(a|b)$,意思是“如果我们知道事件$b$已经发生,事件$a$发生的概率”,或者更简洁地说,“给定$b$的概率”。现在我们可以问一些问题,比如如果昨天下雨,今天下雨的概率是多少$P(今天下雨 | 昨天下雨)$,或者给定患者的测试结果,患者患有该疾病的概率 $P(疾病 | 测试结果)$ 是多少。
|
||
- 在数学上,为了计算给定$b$的条件概率,我们使用公式:$P(a|b)=\frac{P(a\land b)}{P(b)}$
|
||
- 换句话说,给定$b$为真的概率等于$a$并且$b$为真,除以$b$的概率。对此进行推理的一种直观方式是认为“我们对$a$并且$b$都为真的事件(分子)感兴趣,但只对我们知道$b$为真(分母)的世界感兴趣。“除以 $b$ 将可能的世界限制在 $b$ 为真的世界。以下是上述公式的代数等价形式:
|
||
|
||
$P(a\land b)=P(b)P(a|b)$
|
||
|
||
$P(a\land b)=P(a)P(b|a)$
|
||
|
||
- 例如,考虑$P(总和为 12|在一个骰子上掷出 6)$,或者掷两个骰子假设我们已经掷了一个骰子并获得了六,得到十二的概率。为了计算这一点,我们首先将我们的世界限制在第一个骰子的值为六的世界:
|
||
|
||

|
||
|
||
- 现在我们问,在我们将问题限制在(除以$P(6)$,或第一个骰子产生 6 的概率)的世界中,事件 a(和为 12)发生了多少次?
|
||
|
||

|
||
|
||
## 随机变量 (Random Variables)
|
||
|
||
- 随机变量是概率论中的一个变量,它有一个可能取值的域。例如,为了表示掷骰子时的可能结果,我们可以定义一个随机变量 Roll,它可以取值$\set{0,1,2,3,4,5,6}$。为了表示航班的状态,我们可以定义一个变量 flight,它采用$\set{准时、延迟、取消}$的值。
|
||
- 通常,我们对每个值发生的概率感兴趣。我们用概率分布来表示这一点。例如:
|
||
|
||
$P(Flight=准时)=0.6$
|
||
|
||
$P(Flight=延迟)=0.3$
|
||
|
||
$P(Flight=取消)=0.1$
|
||
|
||
- 用文字来解释概率分布,这意味着航班准时的可能性为 60%,延误的可能性为 30%,取消的可能性为 10%。注意,如前所述,所有可能结果的概率之和为 1。
|
||
- 概率分布可以更简洁地表示为向量。例如,$P(Flight)=<0.6,0.3,0.1>$。为了便于解释,这些值有一个固定的顺序(在我们的情况下,准时、延迟、取消)。
|
||
|
||
### 独立性 (Independence)
|
||
|
||
- 独立性是指一个事件的发生不会影响另一个事件发生的概率。例如,当掷两个骰子时,每个骰子的结果与另一个骰子的结果是独立的。用第一个骰子掷出 4 不会影响我们掷出的第二个骰子的值。这与依赖事件相反,比如早上的云和下午的雨。如果早上多云,下午更有可能下雨,所以这些事件是有依赖性的。
|
||
- 独立性可以用数学定义:事件$a$和$b$是独立的,当且仅当$a$并且$b$的概率等于$a$的概率乘以$b$的概率:$P(a∧b)=P(a)P(b)$。
|
||
|
||
## 贝叶斯规则 (Bayes’Rule)
|
||
|
||
- 贝叶斯规则在概率论中常用来计算条件概率。换句话说,贝叶斯规则说,给定$b$条件下$a$的概率等于给定$a$的条件下$b$概率,乘以$b$的概率除以$a$ 的概率。
|
||
- $P(b|a)=\frac{P(a|b)P(b)}{P(a)}$
|
||
- 例如,如果早上有云,我们想计算下午下雨的概率,或者$P(雨 | 云)$。我们从以下信息开始:
|
||
|
||
- 80% 的雨天下午开始于多云的早晨,或$P(云 | 雨)$。
|
||
- 40% 的日子早晨多云,或$P(云)$。
|
||
- 10% 的日子有下雨的下午,或$P(雨)$。
|
||
- 应用贝叶斯规则,我们计算$\frac{0.8*0.1}{0.4}=0.2$。也就是说,考虑到早上多云,下午下雨的可能性是 20%。
|
||
- 除了$P(a)$和$P(b)$之外,知道$P(a|b)$还允许我们计算$P(b|a)$。这是有帮助的,因为知道给定未知原因的可见效应的条件概率$P(可见效应 | 未知原因)$,可以让我们计算给定可见效应的未知原因的概率$P(未知原因 | 可见效应)$。例如,我们可以通过医学试验来学习$P(医学测试结果 | 疾病)$,在医学试验中,我们对患有该疾病的人进行测试,并观察测试结果发生的频率。知道了这一点,我们就可以计算出$P(疾病 | 医学检测结果)$,这是有价值的诊断信息。
|
||
|
||
## 联合概率 (Joint Probability)
|
||
|
||
- 联合概率是指多个事件全部发生的可能性。
|
||
- 让我们考虑下面的例子,关于早上有云,下午有雨的概率。
|
||
|
||
| C=云 | C=$\lnot$云 |
|
||
| ---- | ----------- |
|
||
| 0.4 | 0.6 |
|
||
|
||
| R=雨 | R=$\lnot$雨 |
|
||
| ---- | ----------- |
|
||
| 0.1 | 0.9 |
|
||
|
||
- 从这些数据来看,我们无法判断早上的云是否与下午下雨的可能性有关。为了做到这一点,我们需要看看这两个变量所有可能结果的联合概率。我们可以将其表示在下表中:
|
||
|
||
| | R=雨 | R=$\lnot$ 雨 |
|
||
| ----------- | ---- | ------------ |
|
||
| C=云 | 0.08 | 0.32 |
|
||
| C=$\lnot$云 | 0.02 | 0.58 |
|
||
|
||
- 现在我们可以知道有关这些事件同时发生的信息了。例如,我们知道某一天早上有云,下午有雨的概率是 0.08。早上没有云,下午没有雨的概率是 0.58。
|
||
- 使用联合概率,我们可以推导出条件概率。例如,如果我们感兴趣的是在下午下雨的情况下,早上云层的概率分布。$P(C|雨)=\frac{P(C,雨)}{P(雨)}$旁注:在概率上,逗号和$∧$可以互换使用。因此,$P(C,雨)=P(C\land 雨)$。换句话说,我们将降雨和云层的联合概率除以降雨的概率。
|
||
- 在最后一个方程中,可以将$P(雨)$视为$P(C,雨)$乘以的某个常数$\alpha=\frac{1}{P(雨)}$。因此,我们可以重写$P(C|雨)=\frac{P(C,雨)}{P(雨)}=αP(C,雨)$,或$α<0.08,0.02>=<0.8,0.2>$。考虑到下午有雨,将$α$分解后,我们可以得到 C 的可能值的概率比例。也就是说,如果下午有雨,那么早上有云和早上没有云的概率的比例是$0.08:0.02$。请注意,0.08 和 0.02 的总和不等于 1;然而,由于这是随机变量 C 的概率分布,我们知道它们应该加起来为 1。因此,我们需要通过算$α$来归一化这些值,使得$α0.08+α0.02=1$。最后,我们可以说$P(C|雨)=<0.8,0.2>$。
|
||
|
||
## 概率规则 (Probability Rules)
|
||
|
||
- 否定 (Negation): $P(\lnot a)=1-P(a)$。这源于这样一个事实,即所有可能世界的概率之和为 1,互补事件$\lnot a$和 $a$ 包括所有可能世界。
|
||
- 包含 - 排除 Inclusion-Exclusion:$P(a\lor b)=P(a)+P(b)-P(a\land b)$。这可以用以下方式解释:$a$或$b$为真的世界等于$a$为真的所有世界,加上$b$为真的所有世界。然而,在这种情况下,有些世界被计算两次(a 和$b$都为真的世界)。为了消除这种重叠,我们将$a$和$b$ 都为真的世界减去一次(因为它们被计算了两次)。
|
||
|
||
> 下面是一个例子,可以说明这一点。假设我 80% 的时间吃冰淇淋,70% 的时间吃饼干。如果我们计算今天我吃冰淇淋或饼干的概率,不减去$P(冰淇淋∧饼干)$,我们错误地得出 0.7+0.8=1.5。这与概率在 0 和 1 之间的公理相矛盾。为了纠正我同时吃冰淇淋和饼干的天数计算两次的错误,我们需要减去$P(冰淇淋∧饼干)$一次。
|
||
|
||
- 边缘化 (Marginalization):$P(a)=P(a,b)+P(a,\lnot b)$。这里的观点是,$b$和$\lnot b$是独立的概率。也就是说,$b$和$\lnot b$同时发生的概率为 0。我们也知道$b$和$\lnot b$的总和为 1。因此,当$a$发生时,$b$可以发生也可以不发生。当我们把$a$和$b$发生的概率加上$a$和$\lnot b$的概率时,我们得到的只是$a$ 的概率。
|
||
- 随机变量的边缘化可以用:$P(X=x_i)=\sum_jP(X=x_i,Y=y_j)$表示
|
||
- 方程的左侧表示“随机变量$X$具有$x_i$值的概率”例如,对于我们前面提到的变量 C,两个可能的值是早上有云和早上没有云。等式的正确部分是边缘化的概念。$P(X=x_i)$等于$x_i$以及随机变量$Y$的每一个值的所有联合概率之和。例如,$P(C=云)=P(C=云,R=雨)+P(C=云,R=\lnot 雨)=0.08+0.32=0.4$。
|
||
|
||
- 条件边缘化:$P(a)=P(a|b)P(b)+P(a|\lnot b)P(\lnot b)$。这是一个类似于边缘化的想法。事件$a$发生的概率等于给定$b$的概率乘以$b$的概率,再加上给定$\lnot b$的概率乘以$\lnot b$ 的概率。
|
||
- $P(X=x_i)=\sum_jP(X=x_i|Y=y_i)P(Y=y_i)$
|
||
- 在这个公式中,随机变量$X$取$x_i$值概率等于$x_i$以及随机变量$Y$的每个值的联合概率乘以变量$Y$取该值的概率之和。如果我们还记得$P(a|b)=\frac{P(a,b)}{P(b)}$,就可以理解这个公式。如果我们将这个表达式乘以$P(b)$,我们得到$P(a,b)$,从这里开始,我们做的与边缘化相同。
|
||
|
||
## 贝叶斯网络 (Bayesian Networks)
|
||
|
||
- 贝叶斯网络是一种表示随机变量之间相关性的数据结构。贝叶斯网络具有以下属性:
|
||
|
||
- 它们是有向图。
|
||
- 图上的每个节点表示一个随机变量。
|
||
- 从 X 到 Y 的箭头表示 X 是 Y 的父对象。也就是说,Y 的概率分布取决于 X 的值。
|
||
- 每个节点 X 具有概率分布$P(X|Parents(X))$。
|
||
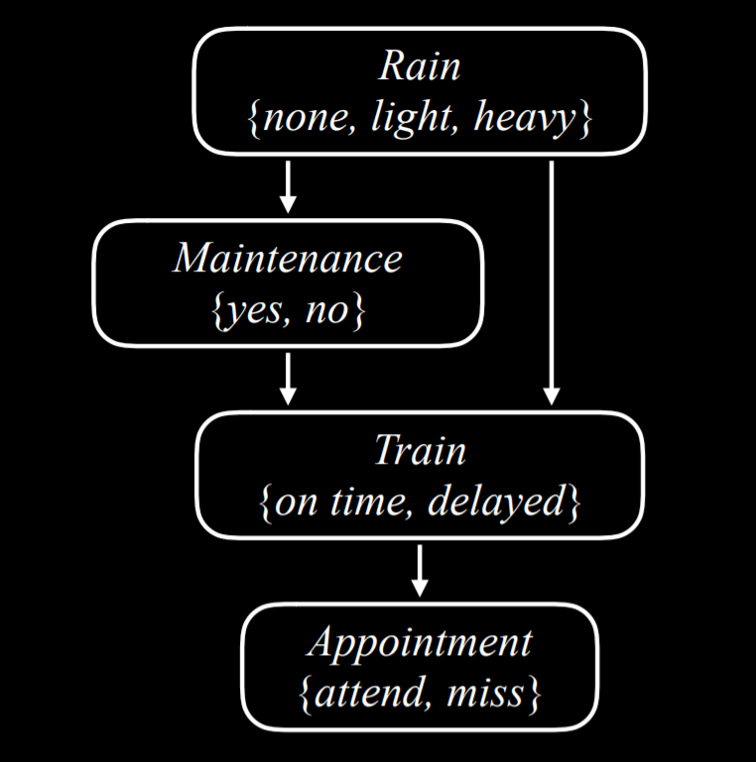
- 让我们考虑一个贝叶斯网络的例子,该网络包含影响我们是否按时赴约的随机变量。
|
||
|
||
|
||
|
||
- 让我们从上到下描述这个贝叶斯网络:
|
||
|
||
- rain 是这个网络的根节点。这意味着它的概率分布不依赖于任何先前的事件。在我们的例子中,Rain 是一个随机变量,可以采用以下概率分布的值$\set{none,light,heavy}$:
|
||
|
||
| none | light | heavy |
|
||
| ---- | ----- | ----- |
|
||
| 0.7 | 0.2 | 0.1 |
|
||
|
||
- Maintenance 对是否有列车轨道维护进行编码,取值为$\set{yes,no}$。Rain 是 Maintenance 的父节点,这意味着 Maintenance 概率分布受到 Rain 的影响。
|
||
|
||
| R | yes | no |
|
||
| ----- | --- | --- |
|
||
| none | 0.4 | 0.6 |
|
||
| light | 0.2 | 0.8 |
|
||
| heavy | 0.1 | 0.9 |
|
||
|
||
- Train 是一个变量,用于编码列车是准时还是晚点,取值为$\set{on\ time,delayed}$。请注意,列车上被“Maintenance”和“rain”指向。这意味着两者都是 Train 的父对象,它们的值会影响 Train 的概率分布。
|
||
|
||
| R | M | On time | Delayed |
|
||
| ------ | --- | ------- | ------- |
|
||
| none | yes | 0.8 | 0.2 |
|
||
| none | no | 0.9 | 0.1 |
|
||
| light | yes | 0.6 | 0.4 |
|
||
| light | no | 0.7 | 0.3 |
|
||
| heavry | yes | 0.4 | 0.6 |
|
||
| heavy | no | 0.5 | 0.5 |
|
||
|
||
- Appointment 是一个随机变量,表示我们是否参加约会,取值为$\set{attend, miss}$。请注意,它唯一的父级是 Train。关于贝叶斯网络的这一点值得注意:父子只包括直接关系。的确,Maintenance 会影响 Train 是否准时,而 Train 是否准时会影响我们是否赴约。然而,最终,直接影响我们赴约机会的是 Train 是否准时,这就是贝叶斯网络所代表的。例如,如果火车准时到达,可能会有大雨和轨道维护,但这对我们是否赴约没有影响。
|
||
|
||
| T | attend | miss |
|
||
| ------- | ------ | ---- |
|
||
| on time | 0.9 | 0.1 |
|
||
| delayed | 0.6 | 0.4 |
|
||
|
||
- 例如,如果我们想找出在没有维护和小雨的一天火车晚点时错过约会的概率,或者$P(light,no,delayed,miss)$,我们将计算如下:$P(light)P(no|light)P(delayed|light,no)P(miss|delayed)$。每个单独概率的值可以在上面的概率分布中找到,然后将这些值相乘以产生$P(light,no,delayed,miss)$。
|
||
|
||
### 推理 (Inference)
|
||
|
||
- 在知识推理,我们通过蕴含来看待推理。这意味着我们可以在现有信息的基础上得出新的信息。我们也可以根据概率推断出新的信息。虽然这不能让我们确切地知道新的信息,但它可以让我们计算出一些值的概率分布。推理具有多个属性。
|
||
- Query 查询变量 $X$:我们要计算概率分布的变量。
|
||
- Evidence variables 证据变量$E$: 一个或多个观测到事件$e$ 的变量。例如,我们可能观测到有小雨,这一观测有助于我们计算火车延误的概率。
|
||
- Hidden variables 隐藏变量 $H$: 不是查询结论的变量,也没有被观测到。例如,站在火车站,我们可以观察是否下雨,但我们不知道道路后面的轨道是否有维修。因此,在这种情况下,Maintenance 将是一个隐藏的变量。
|
||
- The goal 目标:计算$P(X|e)$。例如,根据我们知道有小雨的证据 $e$ 计算 Train 变量 (查询) 的概率分布。
|
||
- 举一个例子。考虑到有小雨和没有轨道维护的证据,我们想计算 Appointment 变量的概率分布。也就是说,我们知道有小雨,没有轨道维护,我们想弄清楚我们参加约会和错过约会的概率是多少,$P(Appointment|light,no)$。从联合概率部分中,我们知道我们可以将约会随机变量的可能值表示为一个比例,将$P(Appointment|light,no)$重写为$αP(Appointment,light,no)$。如果 Appointment 的父节点仅为 Train 变量,而不是 Rain 或 Maintenance,我们如何计算约会的概率分布?在这里,我们将使用边缘化。$P(Appointment,light,no)$的值等于$α[P(Appointment,light,no,delay)+P(Appointment,light,no,on\ time)]$。
|
||
|
||
### 枚举推理
|
||
|
||
- 枚举推理是在给定观测证据$e$和一些隐藏变量$Y$的情况下,找到变量$X$ 的概率分布的过程。
|
||
- $P(X|e)=\alpha P(X,e)=\alpha \sum_yP(X,e,y)$
|
||
- 在这个方程中,$X$代表查询变量,$e$代表观察到的证据,$y$代表隐藏变量的所有值,$α$归一化结果,使我们最终得到的概率加起来为 1。用文字来解释这个方程,即给定$e$的$X$的概率分布等于$X$和$e$的归一化概率分布。为了得到这个分布,我们对$X、e$和$y$的归一化概率求和,其中$y$每次取隐藏变量$Y$ 的不同值。
|
||
- Python 中存在多个库,以简化概率推理过程。我们将查看库 `pomegranate`,看看如何在代码中表示上述数据。
|
||
|
||
```python
|
||
from pomegranate import *
|
||
'''创建节点,并为每个节点提供概率分布'''
|
||
# Rain 节点没有父节点
|
||
rain = Node(DiscreteDistribution({
|
||
"none": 0.7,
|
||
"light": 0.2,
|
||
"heavy": 0.1
|
||
}), name="rain")
|
||
# Track maintenance 节点以 rain 为条件
|
||
maintenance = Node(ConditionalProbabilityTable([
|
||
["none", "yes", 0.4],
|
||
["none", "no", 0.6],
|
||
["light", "yes", 0.2],
|
||
["light", "no", 0.8],
|
||
["heavy", "yes", 0.1],
|
||
["heavy", "no", 0.9]
|
||
], [rain.distribution]), name="maintenance")
|
||
# Train node 节点以 rain 和 maintenance 为条件
|
||
train = Node(ConditionalProbabilityTable([
|
||
["none", "yes", "on time", 0.8],
|
||
["none", "yes", "delayed", 0.2],
|
||
["none", "no", "on time", 0.9],
|
||
["none", "no", "delayed", 0.1],
|
||
["light", "yes", "on time", 0.6],
|
||
["light", "yes", "delayed", 0.4],
|
||
["light", "no", "on time", 0.7],
|
||
["light", "no", "delayed", 0.3],
|
||
["heavy", "yes", "on time", 0.4],
|
||
["heavy", "yes", "delayed", 0.6],
|
||
["heavy", "no", "on time", 0.5],
|
||
["heavy", "no", "delayed", 0.5],
|
||
], [rain.distribution, maintenance.distribution]), name="train")
|
||
# Appointment 节点以列车为条件
|
||
appointment = Node(ConditionalProbabilityTable([
|
||
["on time", "attend", 0.9],
|
||
["on time", "miss", 0.1],
|
||
["delayed", "attend", 0.6],
|
||
["delayed", "miss", 0.4]
|
||
], [train.distribution]), name="appointment")
|
||
'''我们通过添加所有节点来创建模型,然后通过在节点之间添加边来描述哪个节点是另一个节点的父节点(回想一下,贝叶斯网络是一个有向图,节点之间由箭头组成)。'''
|
||
# 创建贝叶斯网络并添加状态
|
||
model = BayesianNetwork()
|
||
model.add_states(rain, maintenance, train, appointment)
|
||
# 添加连接节点的边
|
||
model.add_edge(rain, maintenance)
|
||
model.add_edge(rain, train)
|
||
model.add_edge(maintenance, train)
|
||
model.add_edge(train, appointment)
|
||
# 最终确定模型
|
||
model.bake()
|
||
'''模型可以计算特定条件下的概率'''
|
||
# 计算给定观测的概率
|
||
probability = model.probability([["none", "no", "on time", "attend"]])
|
||
print(probability)
|
||
'''我们可以使用该模型为所有变量提供概率分布,给出一些观测到的证据。在以下情况下,我们知道火车晚点了。给定这些信息,我们计算并打印变量 Rain、Maintenance 和 Appointment 的概率分布。'''
|
||
# 根据火车晚点的证据计算预测
|
||
predictions = model.predict_proba({
|
||
"train": "delayed"
|
||
})
|
||
# 打印每个节点的预测
|
||
for node, prediction in zip(model.states, predictions):
|
||
# 预测已确定时返回字符串
|
||
if isinstance(prediction, str):
|
||
print(f"{node.name}: {prediction}")
|
||
else:
|
||
# 预测不确定时返回概率分布
|
||
print(f"{node.name}")
|
||
for value, probability in prediction.parameters[0].items():
|
||
print(f" {value}: {probability:.4f}")
|
||
```
|
||
|
||
- 上面的代码使用了枚举推理。然而,这种计算概率的方法效率很低,尤其是当模型中有很多变量时。另一种方法是放弃精确推理,转而采用近似推理。这样做,我们在生成的概率中会失去一些精度,但这种不精确性通常可以忽略不计。相反,我们获得了一种可扩展的概率计算方法。
|
||
|
||
### 采样 (Sampling)
|
||
|
||
- 采样是一种近似推理技术。在采样中,根据每个变量的概率分布对其值进行采样。
|
||
|
||
> 要使用骰子采样生成分布,我们可以多次掷骰子,并记录每次获得的值。假设我们把骰子掷了 600 次。我们计算得到 1 的次数,应该大约是 100,然后对其余的值 2-6 重复采样。然后,我们将每个计数除以投掷的总数。这将生成掷骰子的值的近似分布:一方面,我们不太可能得到每个值发生概率为 1/6 的结果(这是确切的概率),但我们会得到一个接近它的值。
|
||
|
||
- 如果我们从对 Rain 变量进行采样开始,则生成的值 none 的概率为 0.7,生成的值 light 的概率为 0.2,而生成的值 heavy 的概率则为 0.1。假设我们的采样值为 none。当我们得到 Maintenance 变量时,我们也会对其进行采样,但只能从 Rain 等于 none 的概率分布中进行采样,因为这是一个已经采样的结果。我们将通过所有节点继续这样做。现在我们有一个样本,多次重复这个过程会生成一个分布。现在,如果我们想回答一个问题,比如什么是$P(Train=on\ time)$,我们可以计算变量 Train 具有准时值的样本数量,并将结果除以样本总数。通过这种方式,我们刚刚生成了$P(Train=on\ {time})$的近似概率。
|
||
|
||
<table>
|
||
<tr>
|
||
<td><img src=https://cdn.xyxsw.site/CreObGAg4oXB0oxe2hMcQbYZnAc.png width=520></td>
|
||
<td><img src=https://cdn.xyxsw.site/Vr96bdSafoV4kBxJ3x2cAU0TnOg.png width=520></td>
|
||
</tr>
|
||
</table>
|
||
|
||
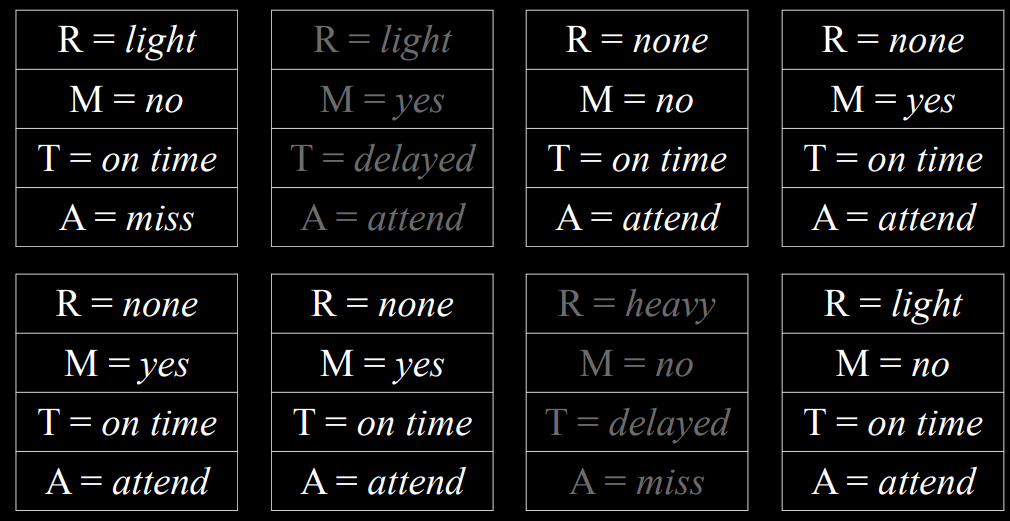
- 我们也可以回答涉及条件概率的问题,例如$P(rain=light|train=on\ {time})$。在这种情况下,我们忽略 Train 值为 delay 的所有样本,然后照常进行。我们计算在$Train=\text{on time}$的样本中有多少样本具有变量$Rain=light$,然后除以$Train=\text{on time}$的样本总数。
|
||
|
||
<table>
|
||
<tr>
|
||
<td><img src=https://cdn.xyxsw.site/KsELbuMTCoKZkGxU9U5czQpanKg.png width=520></td>
|
||
<td><img src=https://cdn.xyxsw.site/MrP0b2FbXofDsOxgnmncufUynAB.png width=520></td>
|
||
</tr>
|
||
</table>
|
||
|
||
| 去除$T= on time$的样本 | 选择$R=light$的样本 |
|
||
| --------------------- | ------------------ |
|
||
|  |  |
|
||
|
||
- 在代码中,采样函数可以是 `generate_sample`:
|
||
|
||
```python
|
||
'''如果你对 pomegrante 库不熟悉,没有关系,考虑 generate_sample 为一个黑盒,或者你可以在 python 解释器中查看 model.states, state.distribution 的值以了解 model 在该库中的实现方式'''
|
||
import pomegranate
|
||
from collections import Counter
|
||
def generate_sample():
|
||
# 随机变量与生成的样本之间的映射
|
||
sample = {}
|
||
# 概率分布与样本的映射
|
||
parents = {}
|
||
# 为所有状态节点采样
|
||
for state in model.states:
|
||
# 如果我们有一个非根节点,则以父节点为条件进行采样
|
||
if isinstance(state.distribution, pomegranate.ConditionalProbabilityTable):
|
||
sample[state.name] = state.distribution.sample(parent_values=parents)
|
||
# 否则,只根据节点的概率分布单独取样
|
||
else:
|
||
sample[state.name] = state.distribution.sample()
|
||
# 追踪映射中的采样值
|
||
parents[state.distribution] = sample[state.name]
|
||
# 返回生成的样本
|
||
return sample
|
||
# 采样
|
||
# 观测到 train=delay,计算 appointment 分布
|
||
N = 10000
|
||
data = []
|
||
# 重复采样 10000 次
|
||
for i in range(N):
|
||
# 根据我们之前定义的函数生成一个样本
|
||
sample = generate_sample()
|
||
# 如果在该样本中,Train 的变量的值为 delay,则保存样本。由于我们对给定 train=delay 的 appointment 概率分布感兴趣,我们丢弃了 train=on time 的采样样本。
|
||
if sample["train"] == "delayed":
|
||
data.append(sample["appointment"])
|
||
# 计算变量的每个值出现的次数。我们可以稍后通过将结果除以保存的样本总数来进行归一化,以获得变量的近似概率,该概率加起来为 1。
|
||
print(Counter(data))
|
||
```
|
||
|
||
### 似然加权
|
||
|
||
- 在上面的采样示例中,我们丢弃了与我们所掌握的证据不匹配的样本。这是低效的。解决这一问题的一种方法是使用似然加权,使用以下步骤:
|
||
|
||
- 首先固定证据变量的值。
|
||
- 使用贝叶斯网络中的条件概率对非证据变量进行采样。
|
||
- 根据其可能性对每个样本进行加权:所有证据出现的概率。
|
||
- 例如,如果我们观察到$Train=\text{on time}$,我们将像之前一样开始采样。我们对给定概率分布的 Rain 值进行采样,然后对 Maintenance 进行采样,但当我们到达 Train 时,我们总是按照观测值取值。然后,我们继续进行,并在给定$Train=\text{on time}$的情况下,根据其概率分布对 Appointment 进行采样。既然这个样本存在,我们就根据观察到的变量在给定其采样父变量的情况下的条件概率对其进行加权。也就是说,如果我们采样了 Rain 并得到了 light,然后我们采样了 Maintenance 并得到了 yes,那么我们将用$P(Train=\text{on time}|light,yes)$来加权这个样本。
|
||
|
||
## 马尔科夫模型 (Markov Models)
|
||
|
||
- 到目前为止,我们已经研究了概率问题,给出了我们观察到的一些信息。在这种范式中,时间的维度没有以任何方式表示。然而,许多任务确实依赖于时间维度,例如预测。为了表示时间变量,我们将创建一个新的变量$X$,并根据感兴趣的事件对其进行更改,使$X_t$ 是当前事件,$X_{t+1}$ 是下一个事件,依此类推。为了能够预测未来的事件,我们将使用马尔可夫模型。
|
||
|
||
### 马尔科夫假设 (<strong>The Markov Assumption</strong>)
|
||
|
||
- 马尔科夫假设是一个假设,即当前状态只取决于有限的固定数量的先前状态。想想预测天气的任务。在理论上,我们可以使用过去一年的所有数据来预测明天的天气。然而,这是不可行的,一方面是因为这需要计算能力,另一方面是因为可能没有关于基于 365 天前天气的明天天气的条件概率的信息。使用马尔科夫假设,我们限制了我们以前的状态(例如,在预测明天的天气时,我们要考虑多少个以前的日子),从而使这个任务变得可控。这意味着我们可能会得到感兴趣的概率的一个更粗略的近似值,但这往往足以满足我们的需要。此外,我们可以根据最后一个事件的信息来使用马尔可夫模型(例如,根据今天的天气来预测明天的天气)。
|
||
|
||
### 马尔科夫链 (<strong>Markov Chain</strong>)
|
||
|
||
- 马尔科夫链是一个随机变量的序列,每个变量的分布都遵循马尔科夫假设。也就是说,链中的每个事件的发生都是基于之前事件的概率。
|
||
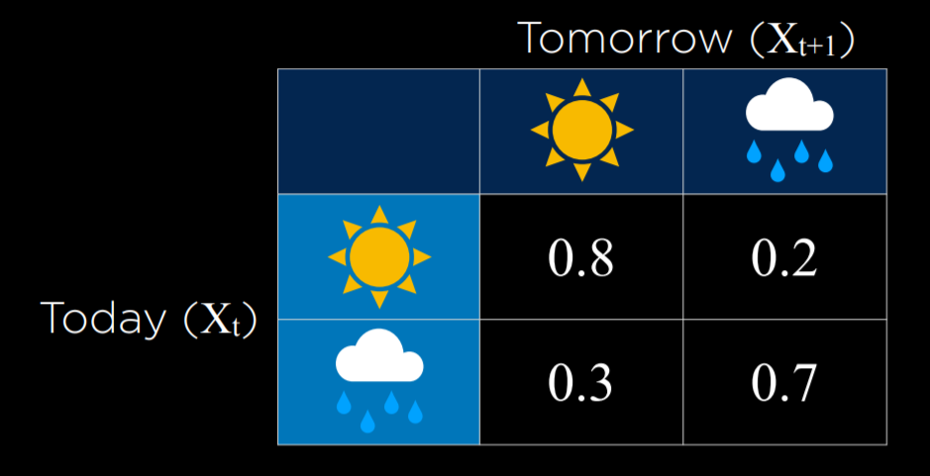
- 为了构建马尔可夫链,我们需要一个过渡模型,该模型将根据当前事件的可能值来指定下一个事件的概率分布。
|
||
|
||
|
||
|
||
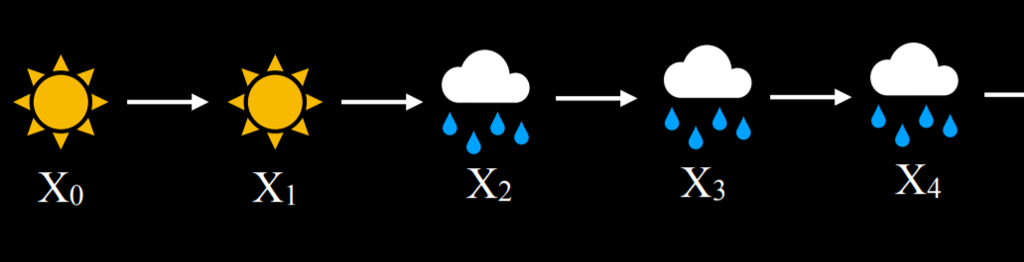
- 在这个例子中,基于今天是晴天,明天是晴天的概率是 0.8。这是合理的,因为晴天之后更可能是晴天。然而,如果今天是雨天,明天下雨的概率是 0.7,因为雨天更有可能相继出现。使用这个过渡模型,可以对马尔可夫链进行采样。从一天是雨天或晴天开始,然后根据今天的天气,对第二天的晴天或雨天的概率进行采样。然后,根据明天的情况对后天的概率进行采样,以此类推,形成马尔科夫链:
|
||
|
||
|
||
|
||
- 给定这个马尔可夫链,我们现在可以回答诸如“连续四个雨天的概率是多少?”这样的问题。下面是一个如何在代码中实现马尔可夫链的例子:
|
||
|
||
```python
|
||
from pomegranate import *
|
||
# 定义起始概率
|
||
start = DiscreteDistribution({
|
||
"sun": 0.5,
|
||
"rain": 0.5
|
||
})
|
||
# 定义过渡模型
|
||
transitions = ConditionalProbabilityTable([
|
||
["sun", "sun", 0.8],
|
||
["sun", "rain", 0.2],
|
||
["rain", "sun", 0.3],
|
||
["rain", "rain", 0.7]
|
||
], [start])
|
||
# 创造马尔科夫链
|
||
model = MarkovChain([start, transitions])
|
||
# 采样 50 次
|
||
print(model.sample(50))
|
||
```
|
||
|
||
## 隐马尔科夫模型 (Hidden Markov Models)
|
||
|
||
- 隐马尔科夫模型是一种具有隐藏状态的系统的马尔科夫模型,它产生了一些观察到的事件。这意味着,有时候,人工智能对世界有一些测量,但无法获得世界的精确状态。在这些情况下,世界的状态被称为隐藏状态,而人工智能能够获得的任何数据都是观察结果。下面是一些这方面的例子:
|
||
|
||
- 对于一个探索未知领域的机器人来说,隐藏状态是它的位置,而观察是机器人的传感器所记录的数据。
|
||
- 在语音识别中,隐藏状态是所讲的话语,而观察是音频波形。
|
||
- 在衡量网站的用户参与度时,隐藏的状态是用户的参与程度,而观察是网站或应用程序的分析。
|
||
- 举个例子。我们的人工智能想要推断天气 (隐藏状态),但它只能接触到一个室内摄像头,记录有多少人带了雨伞。这里是我们的传感器模型 (sensor model),表示了这些概率:
|
||
|
||

|
||
|
||
- 在这个模型中,如果是晴天,人们很可能不会带伞到大楼。如果是雨天,那么人们就很有可能带伞到大楼来。通过对人们是否带伞的观察,我们可以合理地预测外面的天气情况。
|
||
|
||
### 传感器马尔科夫假设
|
||
|
||
- 假设证据变量只取决于相应的状态。例如,对于我们的模型,我们假设人们是否带雨伞去办公室只取决于天气。这不一定反映了完整的事实,因为,比如说,比较自觉的、不喜欢下雨的人可能即使在阳光明媚的时候也会到处带伞,如果我们知道每个人的个性,会给模型增加更多的数据。然而,传感器马尔科夫假设忽略了这些数据,假设只有隐藏状态会影响观察。
|
||
- 隐马尔科夫模型可以用一个有两层的马尔科夫链来表示。上层,变量$X$,代表隐藏状态。底层,变量$E$,代表证据,即我们所拥有的观察。
|
||
|
||
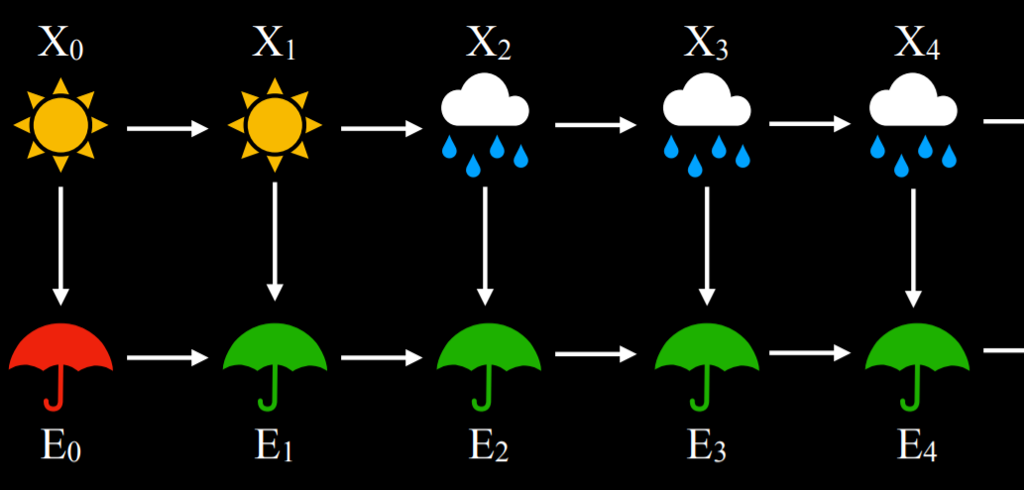
|
||
|
||
- 基于隐马尔科夫模型,可以实现多种任务:
|
||
|
||
- 筛选 Filtering: 给定从开始到现在的观察结果,计算出<strong>当前</strong>状态的概率分布。例如,给从从特定时间开始到今天人们带伞的信息,我们产生一个今天是否下雨的概率分布。
|
||
- 预测 Prediction: 给定从开始到现在的观察,计算<strong>未来</strong>状态的概率分布。
|
||
- 平滑化 Smoothing: 给定从开始到现在的观察,计算<strong>过去</strong>状态的概率分布。例如,鉴于今天人们带了雨伞,计算昨天下雨的概率。
|
||
- 最可能的解释 Most likely explanation: 鉴于从开始到现在的观察,计算最可能的事件顺序。
|
||
- 最可能的解释任务可用于语音识别等过程,根据多个波形,人工智能推断出给这些波形带来的最有可能的单词或音节的序列。接下来是一个隐马尔科夫模型的 Python 实现,我们将用于最可能的解释任务:
|
||
|
||
```python
|
||
from pomegranate import *
|
||
# 每个状态的观测模型
|
||
sun = DiscreteDistribution({
|
||
"umbrella": 0.2,
|
||
"no umbrella": 0.8
|
||
})
|
||
rain = DiscreteDistribution({
|
||
"umbrella": 0.9,
|
||
"no umbrella": 0.1
|
||
})
|
||
states = [sun, rain]
|
||
# 过渡模型
|
||
transitions = numpy.array(
|
||
[[0.8, 0.2], # Tomorrow's predictions if today = sun
|
||
[0.3, 0.7]] # Tomorrow's predictions if today = rain
|
||
)
|
||
# 起始概率
|
||
starts = numpy.array([0.5, 0.5])
|
||
# 建立模型
|
||
model = HiddenMarkovModel.from_matrix(
|
||
transitions, states, starts,
|
||
state_names=["sun", "rain"]
|
||
)
|
||
model.bake()
|
||
```
|
||
|
||
- 请注意,我们的模型同时具有传感器模型和过渡模型。对于隐马尔可夫模型,我们需要这两个模型。在下面的代码片段中,我们看到了人们是否带伞到大楼的观察序列,根据这个序列,我们将运行模型,它将生成并打印出最可能的解释 (即最可能带来这种观察模式的天气序列):
|
||
|
||
```python
|
||
from model import model
|
||
# 观测到的数据
|
||
observations = [
|
||
"umbrella",
|
||
"umbrella",
|
||
"no umbrella",
|
||
"umbrella",
|
||
"umbrella",
|
||
"umbrella",
|
||
"umbrella",
|
||
"no umbrella",
|
||
"no umbrella"
|
||
]
|
||
# 预测隐藏状态
|
||
predictions = model.predict(observations)
|
||
for prediction in predictions:
|
||
print(model.states[prediction].name)
|
||
```
|
||
|
||
- 在这种情况下,程序的输出将是 rain,rain,sun,rain,rain,rain,rain,sun,sun。根据我们对人们带伞或不带伞到大楼的观察,这一输出代表了最有可能的天气模式。
|