34 KiB
一:由不定积分计算定积分
1.1原函数成立区间的问题
注意:由不定积分推导出的原函数在定积分的区间不一定成立!!!
对于大多数定积分题目,可直接由代入不定积分的结论。
二:利用对称性化简定积分
2.1奇偶对称和周期性
命题1:设函数f在区间$[0,a]$可积,且关于区间中点$\frac{a}{2}$为奇函数,即对于$x\in[0,a]$,有$f(x)=-f(a-x)$,则成立
$\int_0^af(x)dx=0$。
命题2:设函数f在区间$[0,a]$可积,且关于区间中点$\frac{a}{2}$为偶函数,即对于$x\in[0,a]$,有$f(x)=f(a-x)$, 则成立
$\int_0^af(x)dx=2\int_0^{\frac{a}{2}}f(x)dx$。
命题3:若函数f为定义在$-\infty<x<+\infty$上的周期为T的连续周期函数,即$f(x)$满足:$f(x)=f(x+T)$,则成立
$\int_a^{a+T}f(x)dx=\int_0^Tf(x)dx$
Proof:
将积分区间拆成多段,带入上文对称公式,之后换元即可,证明的本质是统一了积分区间。
_Example:\int_0^{2\pi}\frac{dx}{sin^4x+cos^4x}
利用:$sin^4x+cos^4x=(sin^2x+cos^2x)^2-2sin^2xcos^2x=1-\frac{1}{2}sin^2(2x)=\frac{1}{2}(1+cos^2(2x))$,周期为$\pi/2$
两次利用命题3,将积分区间化简为$[0,\frac{\pi}{2}]$。由于被积函数关于$\pi/4$偶对称,利用命题2,可将积分区间化简为$[0,\frac{\pi}{4}]$,故原式等于:
$4\int_0^{\frac{\pi}{2}}\frac{dx}{sin^4x+cos^4x}=8\int_0^{\frac{\pi}{4}}\frac{dx}{sin^4x+cos^4x}=16\int_0^{\frac{\pi}{4}}\frac{dx}{1+cos^2(2x)}=8\int_0^{\frac{\pi}{2}}\frac{dt}{1+cos^2(t)}=8\int_0^{\frac{\pi}{2}}\frac{d(tant)}{2+tan^2t}$
$=8\int_{0}^{+\infty}\frac{du}{u^2+2}=4\sqrt{2}arctan(\frac{u}{\sqrt{2}})|0^{+\infty}=2\sqrt{2}\pi$
2.2积分区间的缩小
命题4:设f在$[0,a]$上可积,则成立$\int_0^af(x)dx=\int_0^{\frac{a}{2}}[f(x)+f(a-x)]dx$,此为命题1,2的推广形式。
可推广为:$\int_a^bf(x)dx=\int_a^{\frac{a+b}{2}}[f(x)+f(a+b-x)]dx$,该命题在$f(x)+f(a+b-x)$更好积分时使用。
Proof:
反向利用命题2,$\int_0^af(x)dx=\frac{1}{2}(\int_0^af(x)dx+\int_0^af(a-x)dx)=\int_0^{\frac{a}{2}}[f(x)+f(a-x)]dx$
命题5:若f(x)在闭区间$[0,1]$上连续,则
(a)$\int_0^{\frac{\pi}{2}}f(sinx)dx=\int_0^{\frac{\pi}{2}}f(cosx)dx$
(b)$\int_0^{\pi}xf(sinx)dx=\frac{\pi}{2}\int_0^{\pi}f(sinx)dx$
(c)$\int_0^{\pi}f(sinx)dx=2\int_0^{\frac{\pi}{2}}f(sinx)dx$
Proof:**
(a)$x=\pi/2-t$,(b)$x=\pi-t$,(c)$t=x-\pi/2$
也可由命题4直接推出,如对于(b)
$\int_0^{\pi}(x-\pi/2)f(sinx)dx=\int_0^{\frac{\pi}{2}}(x-\pi/2+\pi-x-\pi/2)f(sinx)dx=0$
Example1:
(a)$\int_0^{\pi/2}\frac{sinx}{sinx+cosx}dx$ (b)$\int_0^{\pi/2}ln(sinx)dx$ (c)$\int_0^{\pi/2}ln(tanx)dx$
(d)$\int_0^{\pi/2}\frac{1}{1+tan^ax}dx$ (e)$\int_0^{\pi}\frac{xsinx}{1+cos^2x}dx$ (f)$\int_0^1\frac{lnx}{\sqrt{1-x^2}}dx$
例如,对于b,利用命题4,$\int_0^{\frac{\pi}{4}}[ln(sin(x))+ln(cos(x))]dx=\int_0^{\frac{\pi}{4}}[ln(sin(2x)/2]dx$
$=\int_0^{\frac{\pi}{4}}[ln(sin(2x))-ln(2)]dx=\frac{1}{2}\int_0^{\frac{\pi}{2}}ln(sin(x))dx-\frac{\pi}{4}ln2=-\frac{\pi}{2}ln2$
Example2:
设$f(x)$在$[a,b]$上连续且单调增加,证明:$\int_a^bxf(x)dx\geq\frac{a+b}{2}\int_a^bf(x)dx$
$\int_a^b(x-\frac{a+b}{2})f(x)dx=\int_a^{\frac{a+b}{2}}[(x-\frac{a+b}{2})f(x)+(a+b-x-\frac{a+b}{2})f(a+b-x)]dx$
$=\int_a^{\frac{a+b}{2}}(x-\frac{a+b}{2})[f(x)-f(a+b-x)]dx$
因为$f(x)$单增,所以$f(x)-f(a+b-x)\leq0$,原式大于等于0,证毕。
三:利用递归表达式化简定积分
注意:全部利用分部积分构造递推表达式,使得分部积分脱出积分号的项为0,对积分内指数进行降阶即可。
3.1高阶三角函数
$I_0=\int_0^{\pi/2}dx=\pi/2$,$I_1=\int_0^{\pi/2}sinxdx=1$,$I_2=\int_0^{\pi/2}sin^2xdx=\pi/4$
思考:如果$I_n$为一数列$I_n=\int_0^{\pi/2}sin^nxdx$,请问
(1)$I_n$的递推表达式为?
(2)$I_n$的通项表达式为?
(3)$I_n(n\to\infty)$的极限为?
(4)求$\lim_{k\to\infty}\frac{I_{2k+1}}{I_{2k}}$?
答案:
(1),(2)

推论:由命题4得,对cosx做上述操作得到结果相同。
(3)$I_n(n\to\infty)$的极限为0,如图为$sin^n(x)在[0,1]$的函数图像,因为$sin^n(x)<x^n<1$,所以函数在[0,1]为0,在x=1处为1,为非一致收敛的情况。,因此分成两段进行证明。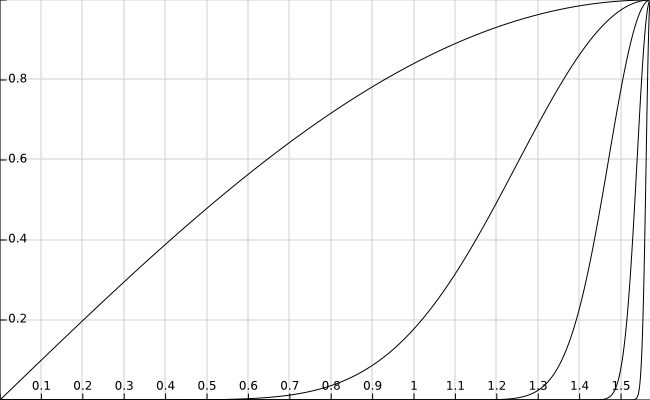
证明:
法一:积分的有界性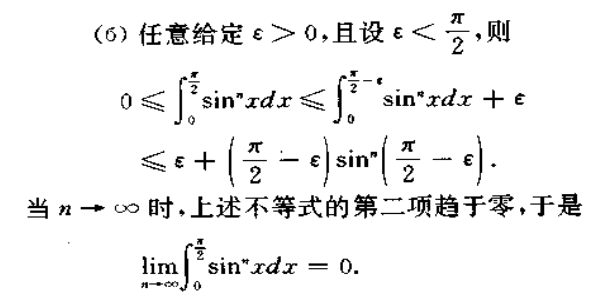
这里第二项趋于0是因为$sin^n(x)\to0$,从图中也可以观察出来。
法二:
$if\ n=2k$
$I_{2k}=\frac{(2k-1)!!}{(2k)!!}=\frac{(2k-1)\cdot(2k-3)\cdot\cdot\cdot5\cdot3\cdot1}{(2k)(2k-2)\cdot\cdot\cdot6\cdot4\cdot2}\cdot\frac{\pi}{2}$
$0<I_{2k}^2=\frac{1\cdot 3}{2^2}\cdot\frac{3\cdot 5}{4^2}\cdot\cdot\frac{(2k-3)(2k-1)}{(2k-2)^2}\cdot \frac{2k-1}{(2k)^2}\cdot\frac{\pi^2}{4}<\frac{2k-1}{(2k)^2}\cdot\frac{\pi^2}{4}\to0$
$\therefore I_{2k}\to0$
$\therefore I_{2k+1}=\int_0^{\pi/2}sinx\cdot sin^{2k}xdx=sinx_0\cdot\int_0^{\pi/2}sin^{2k}xdx\to0$
$\therefore I_{n}\to0$
(4)
维基百科:沃利斯乘积
3B1B:沃利斯乘积的几何解释
3.2组合三角函数
注意:此类题一律用分部积分画出和原被积函数相关的表达式,但不一定是相等,以实现得到递推关系降阶的目的。
Example:
求 $L_n=\int_0^{\pi/2}cos^n(x)cos(nx)dx$ 的递归表达式和通项
$=\frac{1}{n}\int_0^{\pi/2}cos^n(x)dsin(nx)=\frac{1}{n}(cos^n(x)sin(nx)|0^{\pi/2}-\frac{1}{n}\int_0^{\pi/2}nsin(nx)cos^{n-1}(x)(-sin(x))dx$
$=\int_0^{\pi/2}cos^{n-1}(x)sin(nx)sin(x)dx$
$2L_n=\int_0^{\pi/2}[cos^{n-1}(x)sin(nx)sin(x)+cos^n(x)cos(nx)]dx=\int_0^{\pi/2}cos^{n-1}(x)(cos(nx)cos(x)+sin(nx)sin(x))dx$$=\int_0^{\pi/2}cos^{n-1}(x)cos((n-1)x)dx=L{n-1}$
所以 $L_n=\frac{1}{2}L_{n-1}$ 而$L_1=\int_0^{\pi/2}cos(x)cos(x)dx=\pi/4$
所以数列的通项表达式为:L_n=\frac{\pi}{2^{n+1}}
3.3其他函数
Example:
求 $I_n=\int_0^1x^m(ln(x))^ndx$ 的递推表达式和通项。
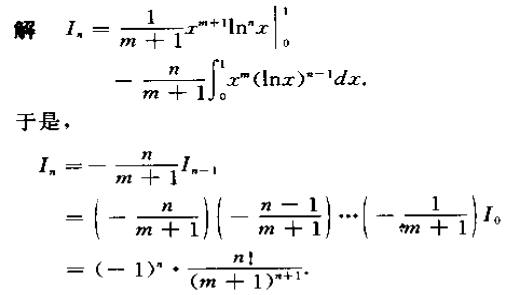
Exercise:
_ (3)求$a_n$的极限
(3)求$a_n$的极限
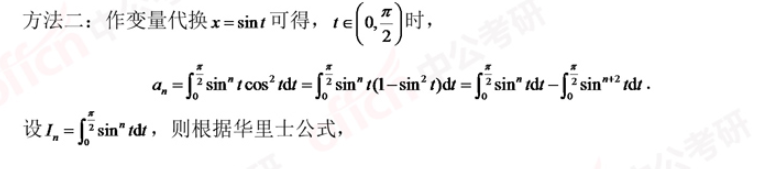

(3)结果为0,证法和高阶三角函数一样。
四:利用级数对定积分进行估值
4.1常用的几种级数
基本的思路是:把函数做泰勒展开,交换积分和求和符号,对每一项幂函数进行积分,最后合并即可。
下面给出三个重要常数:
(a)$\sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}$ (b)$\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}=ln2$ (c)\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{(2m-1)^2}\approx0.92
此类级数可由初等函数泰勒展开后将x=1或x=-1代入得到。
这里给出简单的证明:
(a)$\sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}$
(b)$\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}=ln2$ 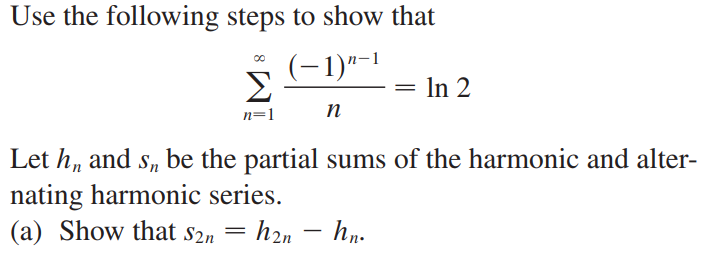
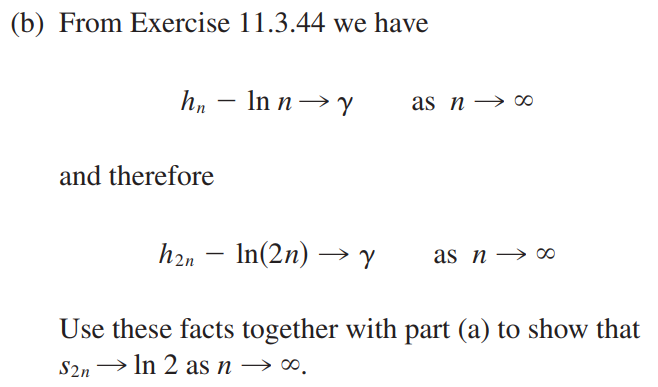
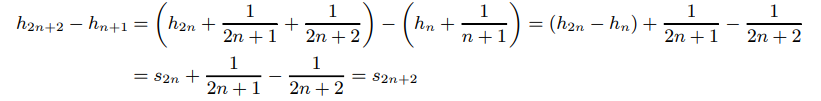
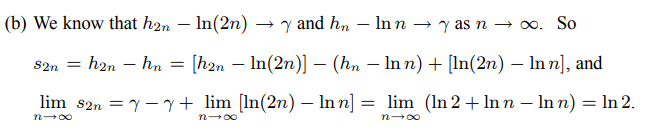
(c)$\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{(2m-1)^2}\approx0.92$
$\int_0^1\frac{arctan(x)}{x}dx=\int_0^1\frac{1}{x}\sum_{n=0}^{\infty}(-1)^n\frac{1}{2n+1}x^{2n+1}dx=\int_0^1\sum_{n=0}^{\infty}(-1)^n\frac{1}{2n+1}x^{2n}dx=\sum_{n=0}^{\infty}(-1)^n\frac{1}{2n+1}\int_0^1x^{2n}dx$$\sum_{n=0}^{\infty}(-1)^n\frac{1}{(2n+1)^2}x^{2n+1}|0^1=\sum{n=0}^{\infty}(-1)^n\frac{1}{(2n+1)^2}=G\approx0.92$ (这可以利用计算机对此积分估值得到)
在计算积分时,通常通过上述思路把积分化为上述重要常数,进而直接得出结果。
4.2将定积分转换为级数
Example1:重要常数(a)
$\int_0^1ln(x)ln(1-x)dx$
答案:
视频链接
Example2:重要常数(c)
(a) $\int_0^{\pi/4}ln(tan(x))dx$ (b) $\int_0^{\pi/4}ln(cot(x))dx$
对于(a),令$t=tan(x)$ ,换元后可得:\int_0^1ln(t)d arctan(t)=[ln(t)arctan(t)]|_0^1-\int_0^1arctant\frac{dt}{t}=-\int_0^1arctant\frac{dt}{t}=-G\approx-0.92
五:特殊积分
5.1伽马函数

维基百科点击下方链接:
WIKI百科
下面为详细的视频教程
1:定义伽马函数
视频链接
2:$(\frac{1}{2})!$
视频链接
3:$(-1)!$
视频链接
4:$n!!$
视频链接
5.2分段函数积分
此类题目的关键是原函数的连续性要求,通过待定系数求解,具体见不定积分中的特殊积分部分。
5.3变限积分
形如$I(x)=\int_a^xf(t)dt$ 的积分叫做变限积分,他的本质是一个自变量在积分限的函数。
变限积分的求导法则尤其重要。此类题目需要扎实的数学分析思想,极其易错,具体内容见积分证明框架。
5.4反常积分
具体内容见积分证明框架
六:定积分的应用
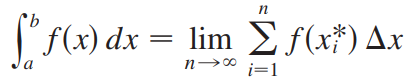
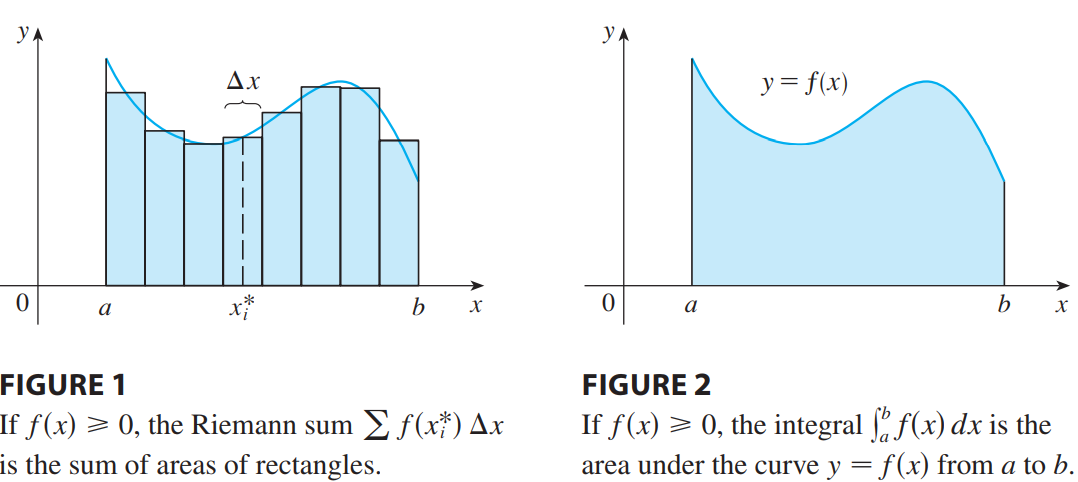
我们可以看到定积分的本质就是微元法取极限,所以一些几何和物理问题都可以用微元法的思想解决。
Example1:
已知一段半圆弧电荷密度为+1,计算圆心处的电场强度。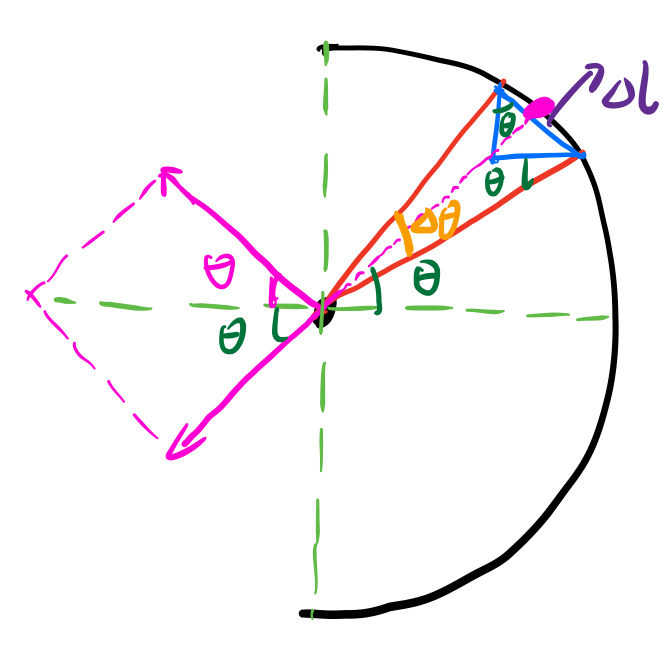
注意,这类题目直接用几何解法更快,由库仑定律得,两段对称的微弧对圆心的电场作用为:
$\Delta E=2\Delta E'cos\theta=\frac{2k\Delta lcos\theta}{R^2}=\frac{2k\Delta r}{R^2}$
$\Delta r$代表上图小三角形垂直部分,$\sum \Delta r=R$ ,所以:
$E=\sum\Delta E=\frac{2k}{R^2}\sum\Delta r=\frac{2k}{R}$
Example2:
我们可以利用微元法找到极坐标的面积公式

6.1几何问题
6.1.1向量簇
请下载:New horizons in geometry(几何新视野).pdf阅读第一章。
这里只讲一个拓扑定理:切线向量扫过的面积等于将这些向量在不改变方向和长度的情况下,将所有的向量尾部接到一起时所组成的图形的面积相等。即切线扫过的面积等于切线簇的面积,如图所示。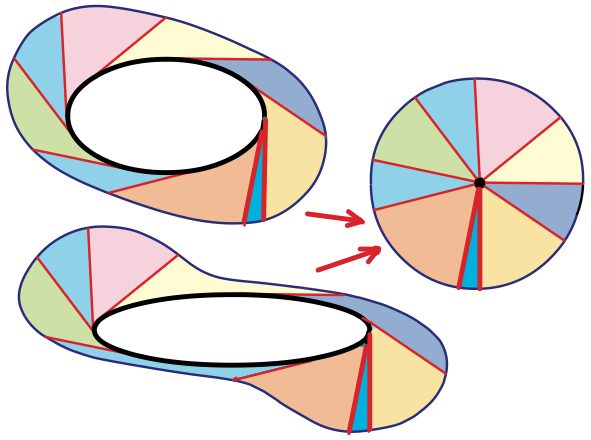
想象一辆自行车,其尾部车轮始终与某一闭合轨迹相切,也就是骑了一圈,那么无论骑行轨迹如何,自行车车身划过的面积始终不变。如上图所示,将一簇切线在不改变方向和长度的情况下尾部连接在一起,他们所组成的形状面积和原来扫过的面积相同,且原来图形的形状可以任意。
和开普勒第二定律及椭圆面积的关系:视频链接
Example3:
利用该定理证明$\int_{-\infty}^{x}e^{t/b}dt=be^{x/b}$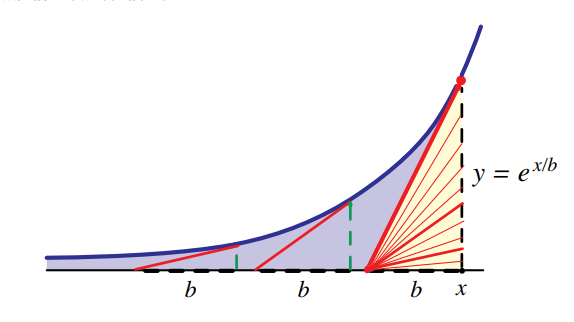
显然,所有切线构成的三角形底边长度都是1,把所有的切线全部放到黄色三角形内,尾部连接在一起,就得到积分的面积是两倍三角形的面积,即$be^{x/b}$。
Example4:
利用该定理求摆线下方的面积。
摆线相关知识点击:维基百科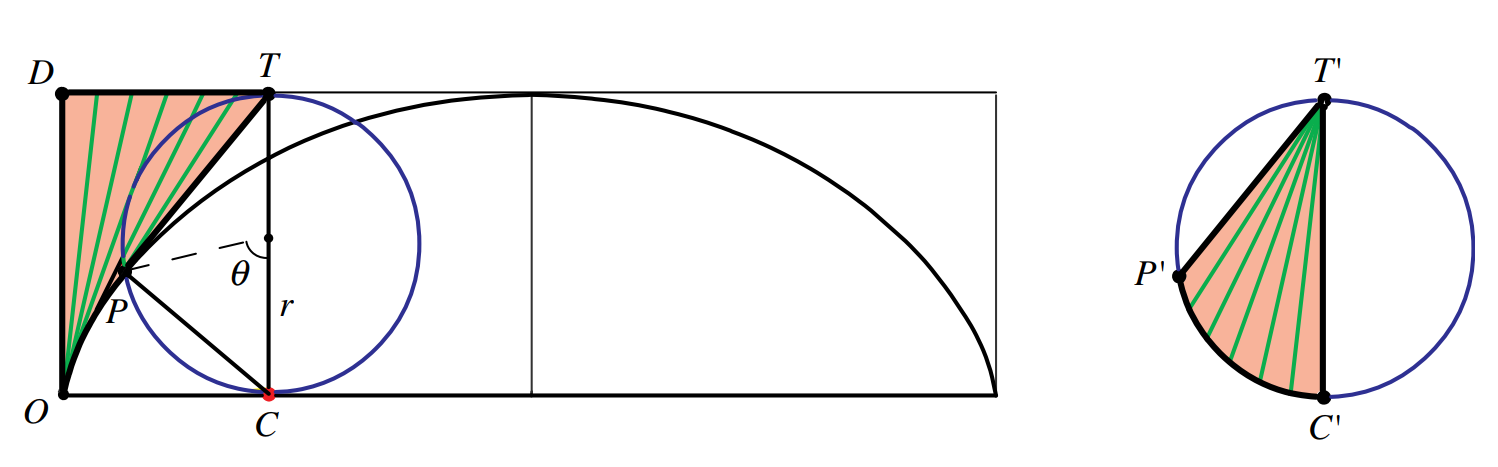
由于PT垂直于PC(在圆内),又因为点P在每个瞬时相对于点C做圆周运动,所以PT必然是点P的切向运动方向,所以PT也是摆线的切线,DOT的面积(及切线扫过的面积)等于右图中切线簇的面积(将所有切线平移到点T)。更具体的说,圆在运动时,点P划过了一段圆弧,在每一个中间点,都可以做线段PT,线段PT既扫过了DOT,也同时覆盖了T'P'C',故两者面积相等。
当圆旋转一周时,切线划过了整个摆线上方的面积,这面积等于切线簇的面积$\pi R^2$,而整个矩形的面积是$2\pi R\cdot 2R=4\pi R^2$,所以摆线下方的面积为$4\pi R^2-\pi R^2=3\pi R^2$。
利用参数方程的证明方法见下文。
6.1.2体积
这里依然是微元法,我们讲两种求旋转体体积的方法:切片法和圆柱法
切片法: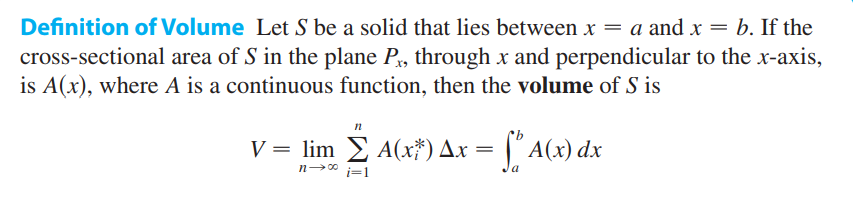
A(x)就是x处物体的面积,$\Delta x$就是高度,两者相乘就是和x有关的一个体积微元,求和或积分后就得到了整个体积。
Example5:
求$y=x$和$y=x^2$中间的部分绕$y=2$旋转一周所得到的图像的体积。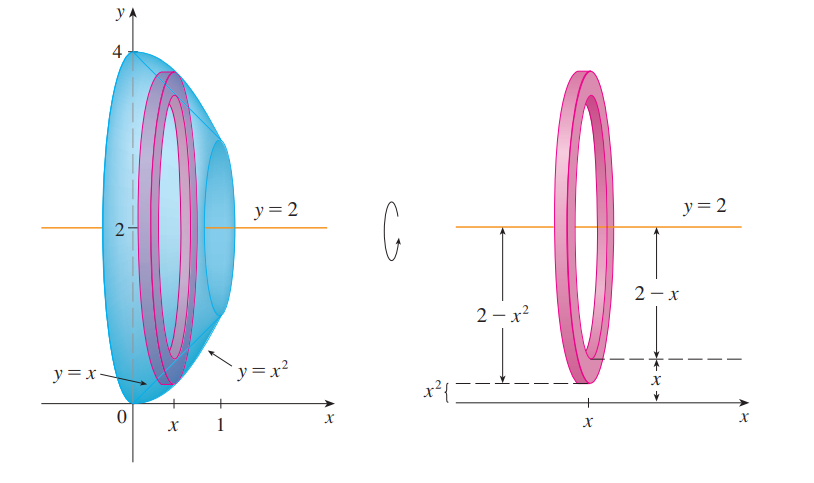
本题的关键是千万不要把正负号弄错,x和y的正负号永远是对原始图像而言的!!!
Example6:
求$y=x$和$y=x^2$中间的部分绕$x=-1$旋转一周所得到的图像的体积。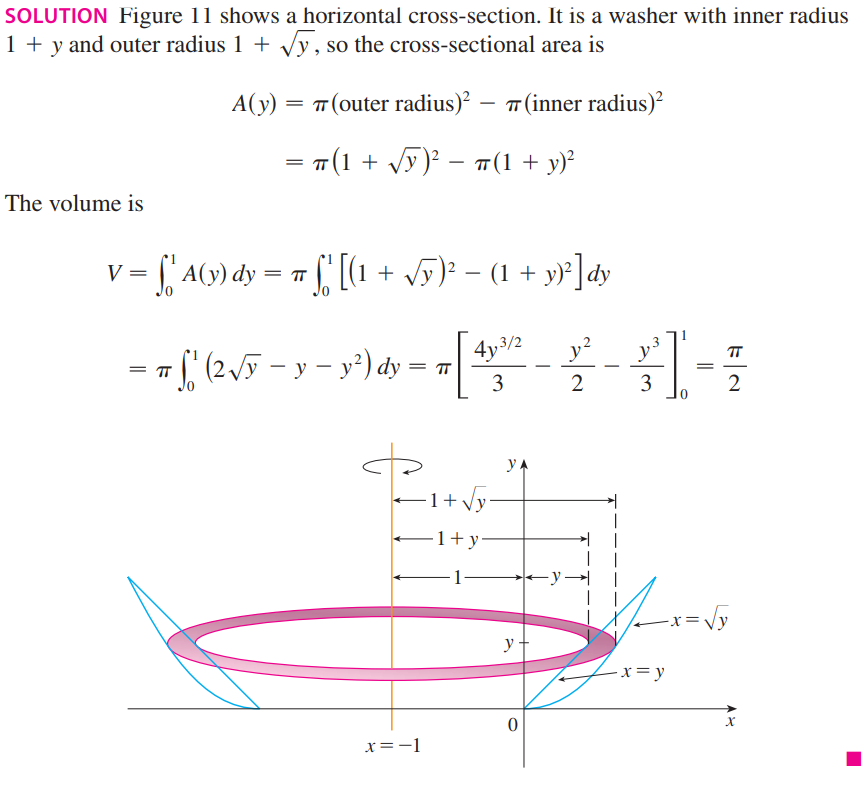
圆柱法: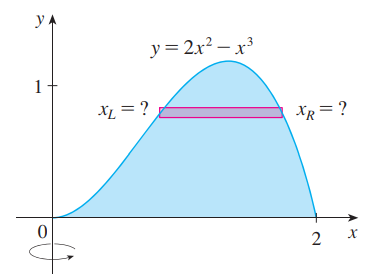
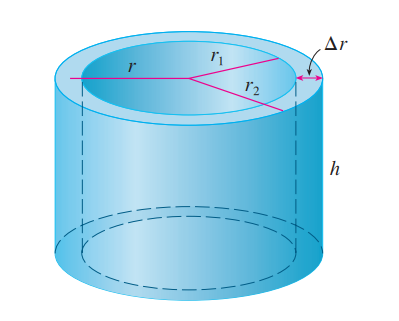
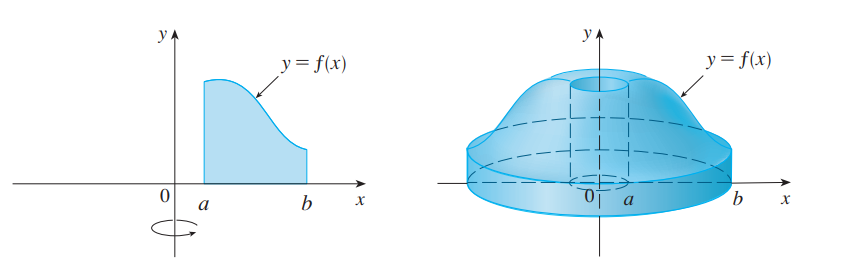
如图所示,$x_L和x_R$比较难求,当边界无法被解析式表达时,我们对垂直于旋转轴的底面做圆柱分解。
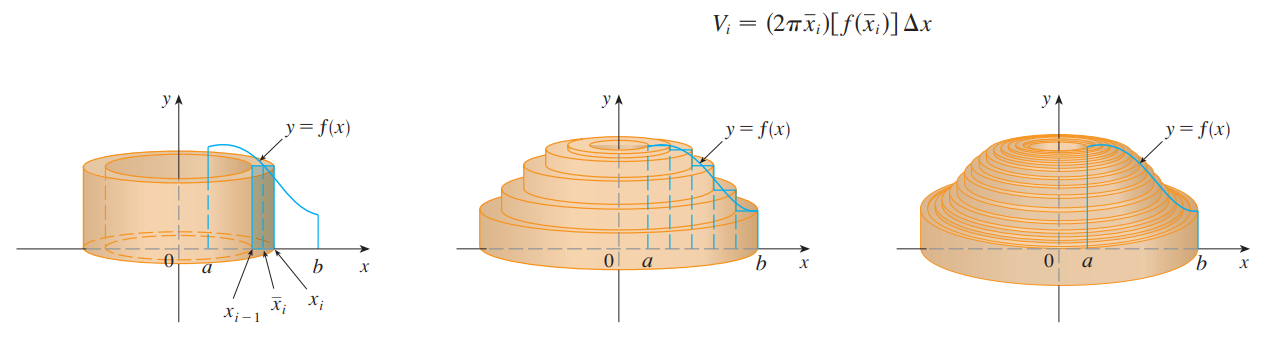

一小段圆柱的体积=底面积:$2\pi xdx$ 乘以 高:$f(x)$,之后对自变量求积分。
Example7:
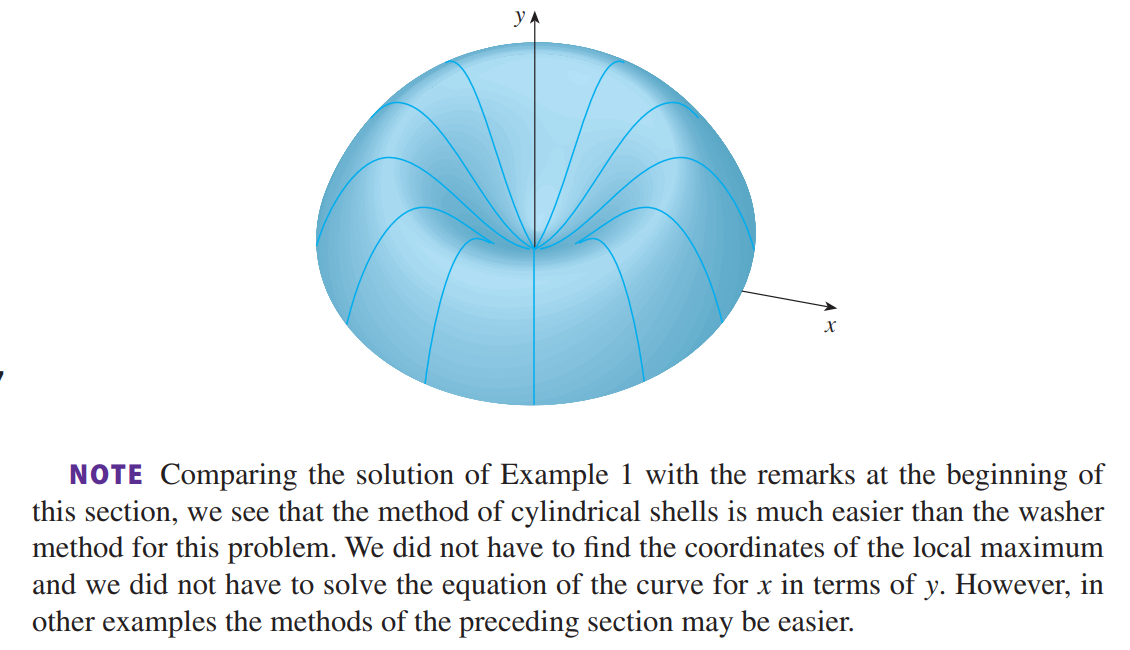
注意:在本题中,圆柱法比切片法简单的多,由于不用求边界,对于具体的题目,根据情况选择两种方法即可。_
6.1.3弧长和表面积
求弧长的方法十分显然,该方法也适用于极坐标,只需用微元法得到公式。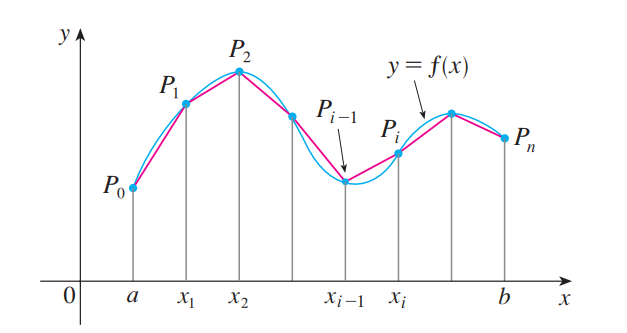
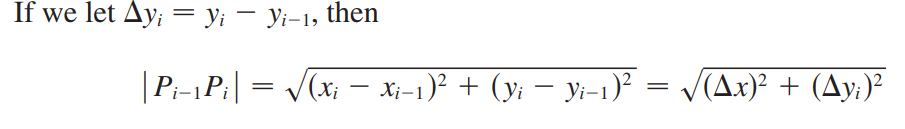

求表面积的方法也是微元法,如下图所示: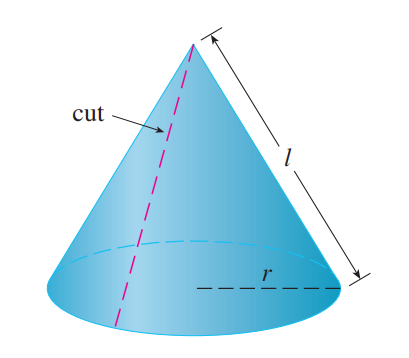
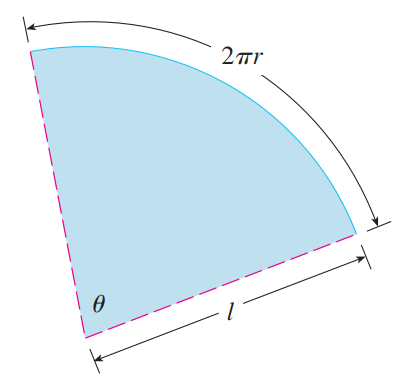
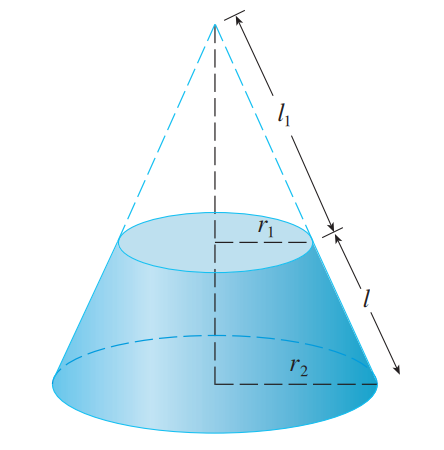
已知圆锥表面积是$\pi rl$,现在试图求解一段圆台的表面积,它等于两个圆锥相减。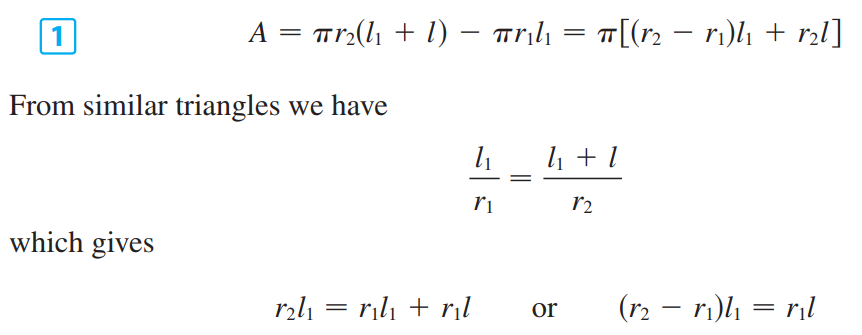

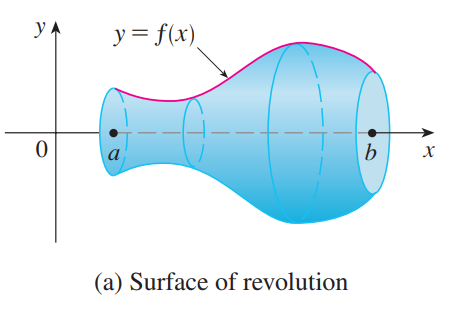
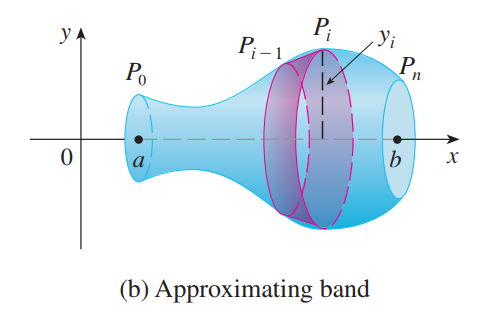
如上图所示,将任意旋转体分成无数小圆台,进行求和即可(这里为什么不能用圆柱做微元法?)。
最后我们得到了表面积的表达式:
Example8:
6.1.4极坐标和参数方程
参数方程:
参数方程本质就是把x和y想成某个变量t的函数,利用链式法则可以把微积分的计算用参数方程实现。
微分: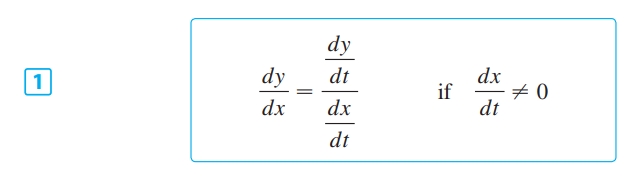
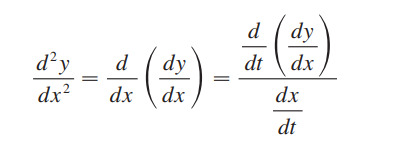
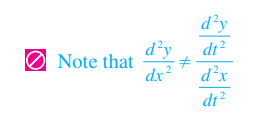
求面积: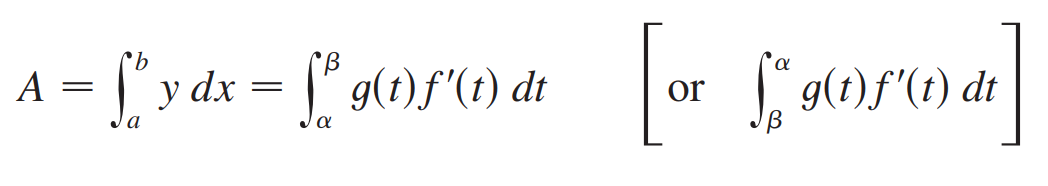
求长度:
Example9:
我们以摆线为例,将摆线方程建模为关于转动角度的函数,如下图所示。
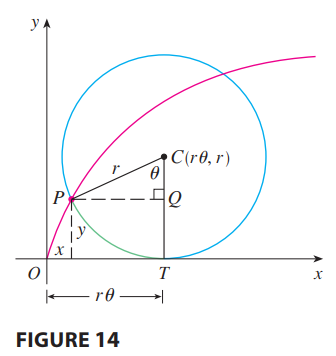

摆线的面积:方法只是简单的换元。
摆线的周长:
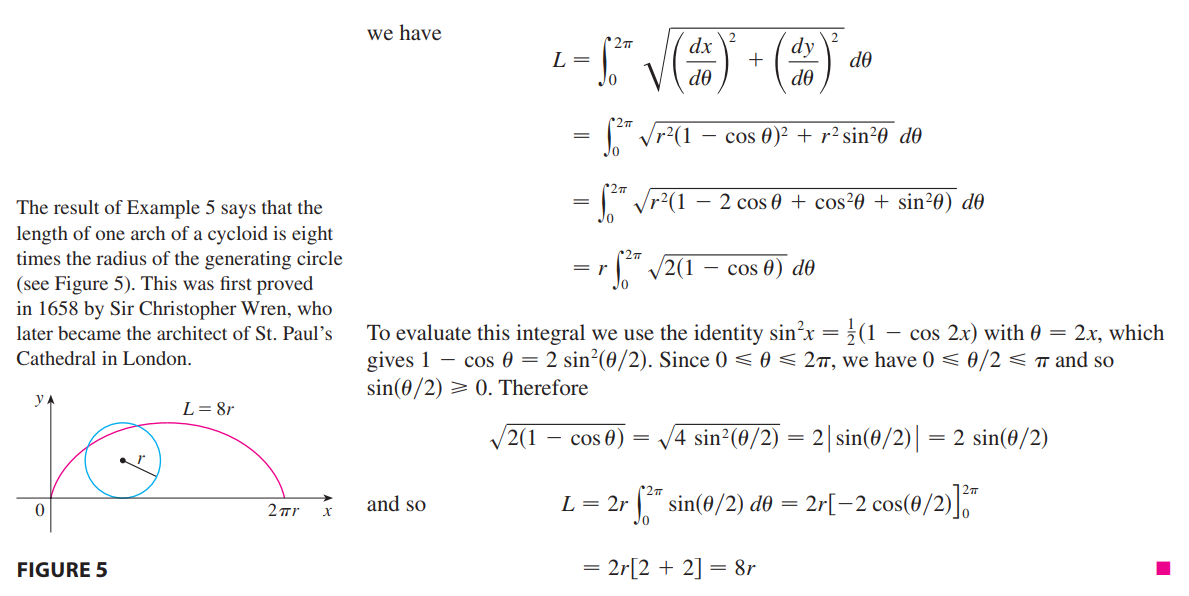
摆线相关知识点击:维基百科
摆线的本质是最速降线,请看3B1B的视频:视频链接
另一个相关视频:费马小定理
极坐标:
极坐标求面积公式前面已给出: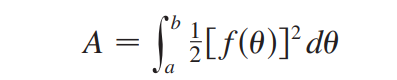
求弧长的公式推导依然是微元法: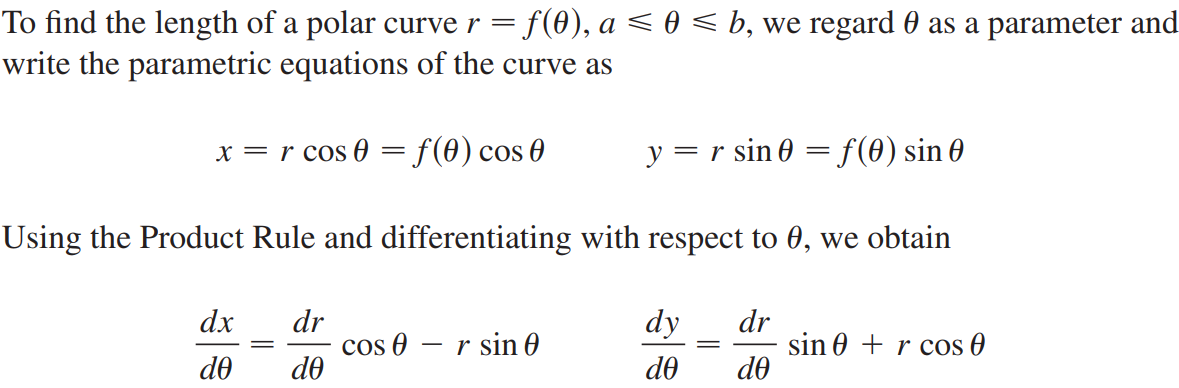

更直观的方法是:弧长显然等于径向速度与法向速度之和。$\Delta l=\sqrt{(dr)^2+(rd\theta)^2}$
Example10:
6.2物理问题
6.2.1质心
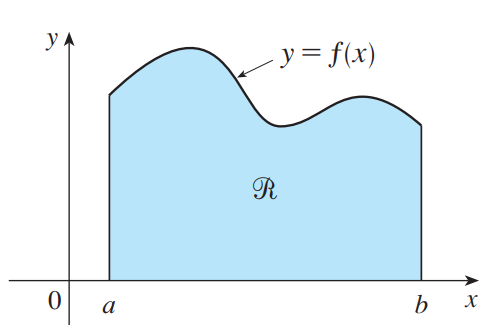
质心和势相关,是力学中研究旋转的概念,质心和势一般来说是对于某个转轴的定义。
质心是一个点,在这点上施加外力不会引起系统的旋转。
势是物体旋转的惯性,表示在施加外力后系统旋转的能力。
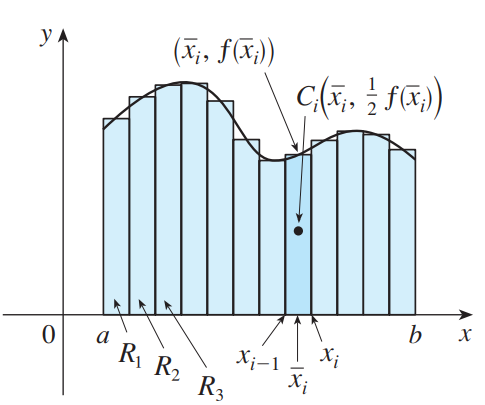
如上图所示,区域R具有恒定密度,它相对于y轴和x轴的势计算方法如下: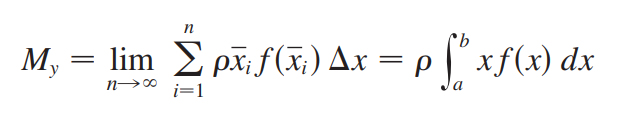 (相当于每个矩形到y轴距离x乘以每个矩形面积f(x)dx)
(相当于每个矩形到y轴距离x乘以每个矩形面积f(x)dx)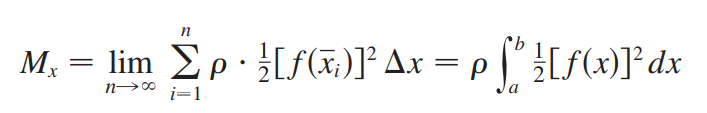 (相当于每个矩形中点到x轴距离f(x)/2乘每个矩形面积f(x)dx)
(相当于每个矩形中点到x轴距离f(x)/2乘每个矩形面积f(x)dx)
上式除以总质量就得到了质心: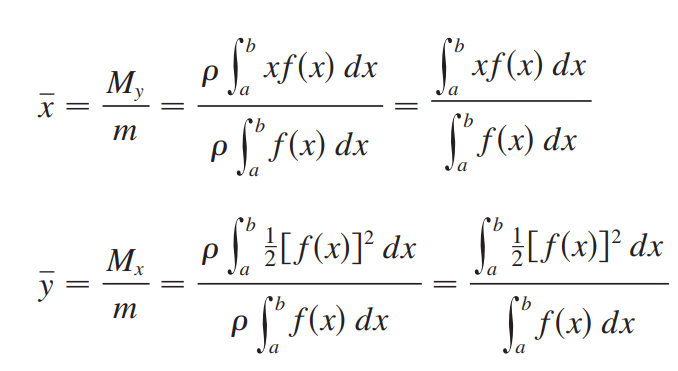
Example12:
6.2.2电磁场
Example13:
一根电荷密度为+1的,长度为L的直导体棒,求距离其中点a的一点的电场强度。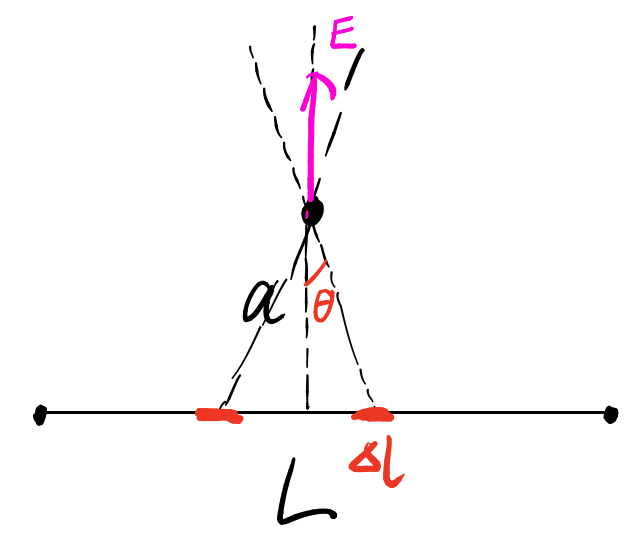
提示:第一种做法是通过微元法转换成积分,第二种做法是找出与其等价的圆弧。
答案:点击链接
6.3一题十解
Example14:
求$Ax^2+2Bxy+Cy^2=1(A>0,AC-B^2>0)$所围图形的面积。
解1: