chore: change pic to cos

8.基础学科/8.2定积分.md

@@ -1,5 +1,5 @@
 本文主要讲解定积分在计算时运用的各种化简技巧。
-![](https://hdu-cs-wiki.oss-cn-hangzhou.aliyuncs.com/lake_card_mindmap.png)
+![](https://pic-hdu-cs-wiki-1307923872.cos.ap-shanghai.myqcloud.com/lake_card_mindmap.png)
 
 # 一：由不定积分计算定积分
 
@@ -14,7 +14,7 @@
 
 ## 2.1奇偶对称和周期性
 
-![](https://hdu-cs-wiki.oss-cn-hangzhou.aliyuncs.com/picture1.png)
+![](https://pic-hdu-cs-wiki-1307923872.cos.ap-shanghai.myqcloud.com/picture1.png)
 <br />
 命题1：设函数f在区间$[0,a]$可积，且关于区间中点$\frac{a}{2}$为奇函数，即对于$x\in[0,a]$，有$f(x)=-f(a-x)$，则成立<br />$\int_0^af(x)dx=0$。<br />命题2：设函数f在区间$[0,a]$可积，且关于区间中点$\frac{a}{2}$为偶函数，即对于$x\in[0,a]$，有$f(x)=f(a-x)$， 则成立<br />$\int_0^af(x)dx=2\int_0^{\frac{a}{2}}f(x)dx$。<br />命题3：若函数f为定义在$-\infty<x<+\infty$上的周期为T的连续周期函数，即$f(x)$满足：$f(x)=f(x+T)$，则成立<br />$\int_a^{a+T}f(x)dx=\int_0^Tf(x)dx$<br />**_Proof：_**<br />将积分区间拆成多段，带入上文对称公式，之后换元即可，证明的本质是统一了积分区间。<br />_**Example：**<br />$\int_0^{2\pi}\frac{dx}{sin^4x+cos^4x}$
 
@@ -30,7 +30,7 @@
 
 ## 3.1高阶三角函数
 $I_0=\int_0^{\pi/2}dx=\pi/2$，$I_1=\int_0^{\pi/2}sinxdx=1$，$I_2=\int_0^{\pi/2}sin^2xdx=\pi/4$<br />思考：如果$I_n$为一数列$I_n=\int_0^{\pi/2}sin^nxdx$，请问<br />（1）$I_n$的递推表达式为？<br />（2）$I_n$的通项表达式为？<br />（3）$I_n(n\to\infty)$的极限为？<br />（4）求$\lim_{k\to\infty}\frac{I_{2k+1}}{I_{2k}}$？<br />答案：<br />（1），（2）<br />
-![](https://hdu-cs-wiki.oss-cn-hangzhou.aliyuncs.com/picture2.png)
+![](https://pic-hdu-cs-wiki-1307923872.cos.ap-shanghai.myqcloud.com/picture2.png)
 
 推论：由命题4得，对cosx做上述操作得到结果相同。<br />（3）$I_n(n\to\infty)$的极限为0，如图为$sin^n(x)在[0,1]$的函数图像，因为$sin^n(x)<x^n<1$，所以函数在[0,1]为0，在x=1处为1，为非一致收敛的情况。，因此分成两段进行证明。<br />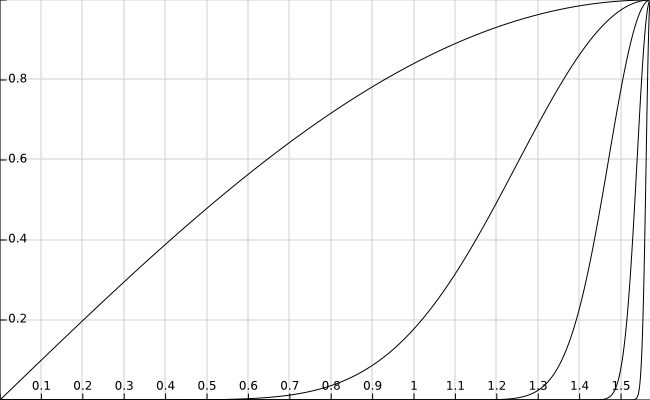![save.png](https://cdn.nlark.com/yuque/0/2019/png/422826/1564801370246-b0067524-94bb-4de3-9d1d-fde22a35d9bf.png#align=left&display=inline&height=158&name=save.png&originHeight=400&originWidth=650&size=32867&status=done&style=none&width=256)<br />证明：<br />法一：积分的有界性<br />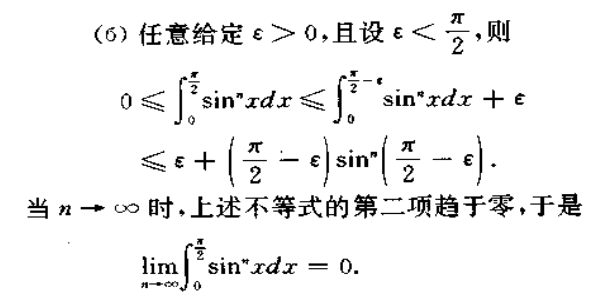![image.png](https://cdn.nlark.com/yuque/0/2019/png/422826/1564497996832-07ba349b-e630-4e23-a0ae-781051191e00.png#align=left&display=inline&height=165&name=image.png&originHeight=295&originWidth=596&size=39253&status=done&style=none&width=333)<br />这里第二项趋于0是因为$sin^n(x)\to0$，从图中也可以观察出来。<br />法二：<br />$if\ n=2k$<br />$I_{2k}=\frac{(2k-1)!!}{(2k)!!}=\frac{(2k-1)\cdot(2k-3)\cdot\cdot\cdot5\cdot3\cdot1}{(2k)(2k-2)\cdot\cdot\cdot6\cdot4\cdot2}\cdot\frac{\pi}{2}$<br />$0<I_{2k}^2=\frac{1\cdot 3}{2^2}\cdot\frac{3\cdot 5}{4^2}\cdot\cdot\frac{(2k-3)(2k-1)}{(2k-2)^2}\cdot \frac{2k-1}{(2k)^2}\cdot\frac{\pi^2}{4}<\frac{2k-1}{(2k)^2}\cdot\frac{\pi^2}{4}\to0$<br />$\therefore I_{2k}\to0$<br />$\therefore I_{2k+1}=\int_0^{\pi/2}sinx\cdot sin^{2k}xdx=sinx_0\cdot\int_0^{\pi/2}sin^{2k}xdx\to0$<br />$\therefore I_{n}\to0$<br />（4）<br />![image.png](https://cdn.nlark.com/yuque/0/2019/png/422826/1564147108664-81bb7241-200a-4d44-bc2c-d054f460cf32.png#align=left&display=inline&height=87&name=image.png&originHeight=202&originWidth=1071&size=42020&status=done&style=none&width=462)<br />维基百科：[沃利斯乘积](https://zh.wikipedia.org/wiki/%E6%B2%83%E5%88%A9%E6%96%AF%E4%B9%98%E7%A7%AF)<br />3B1B：[沃利斯乘积的几何解释](https://www.bilibili.com/video/av22808876/)