🐞 fix(4.3人工智能导论及机器学习): 按照CS50AI课程note格式化文档
删除了大量“无辜”的无序列表
This commit is contained in:
@@ -51,7 +51,7 @@ class StackFrontier: # 堆栈边域
|
|||||||
|
|
||||||
## 深度优先搜索复习
|
## 深度优先搜索复习
|
||||||
|
|
||||||
- 深度优先搜索算法在尝试另一个方向之前耗尽每个方向。在这些情况下,边域作为堆栈数据结构进行管理。这里需要记住的流行语是“后进先出”。在将节点添加到边域后,第一个要删除和考虑的节点是最后一个要添加的节点。这导致了一种搜索算法,该算法在第一个方向上尽可能深入,直到尽头,同时将所有其他方向留到后面。“不撞南墙不回头”
|
深度优先搜索算法在尝试另一个方向之前耗尽每个方向。在这些情况下,边域作为堆栈数据结构进行管理。这里需要记住的流行语是“后进先出”。在将节点添加到边域后,第一个要删除和考虑的节点是最后一个要添加的节点。这导致了一种搜索算法,该算法在第一个方向上尽可能深入,直到尽头,同时将所有其他方向留到后面。“不撞南墙不回头”
|
||||||
|
|
||||||
## 队列边域——BFS
|
## 队列边域——BFS
|
||||||
|
|
||||||
@@ -68,7 +68,7 @@ class QueueFrontier(StackFrontier): # 队列边域
|
|||||||
|
|
||||||
## 广度优先搜索复习
|
## 广度优先搜索复习
|
||||||
|
|
||||||
- 广度优先搜索算法将同时遵循多个方向,在每个可能的方向上迈出一步,然后在每个方向上迈出第二步。在这种情况下,边域作为队列数据结构进行管理。这里需要记住的流行语是“先进先出”。在这种情况下,所有新节点都会排成一行,并根据先添加的节点来考虑节点(先到先得!)。这导致搜索算法在任何一个方向上迈出第二步之前,在每个可能的方向上迈出一步。
|
广度优先搜索算法将同时遵循多个方向,在每个可能的方向上迈出一步,然后在每个方向上迈出第二步。在这种情况下,边域作为队列数据结构进行管理。这里需要记住的流行语是“先进先出”。在这种情况下,所有新节点都会排成一行,并根据先添加的节点来考虑节点(先到先得!)。这导致搜索算法在任何一个方向上迈出第二步之前,在每个可能的方向上迈出一步。
|
||||||
|
|
||||||
## 迷宫解——Maze_solution
|
## 迷宫解——Maze_solution
|
||||||
|
|
||||||
|
|||||||
@@ -13,48 +13,50 @@
|
|||||||
|
|
||||||
## 理解
|
## 理解
|
||||||
|
|
||||||
- 这个项目有两个主要文件:`runner.py` 和 `tictactoe.py`。`tictactoe.py` 包含了玩游戏和做出最佳动作的所有逻辑。`runner.py` 已经为你实现,它包含了运行游戏图形界面的所有代码。一旦你完成了 `tictactoe.py` 中所有必需的功能,你就可以运行 `python runner.py` 来对抗你的人工智能了!
|
这个项目有两个主要文件:`runner.py` 和 `tictactoe.py`。`tictactoe.py` 包含了玩游戏和做出最佳动作的所有逻辑。`runner.py` 已经为你实现,它包含了运行游戏图形界面的所有代码。一旦你完成了 `tictactoe.py` 中所有必需的功能,你就可以运行 `python runner.py` 来对抗你的人工智能了!
|
||||||
- 让我们打开 `tictactoe.py` 来了解所提供的内容。首先,我们定义了三个变量:X、O 和 EMPTY,以表示游戏的可能移动。
|
|
||||||
- 函数 `initial_state` 返回游戏的启动状态。对于这个问题,我们选择将游戏状态表示为三个列表的列表(表示棋盘的三行),其中每个内部列表包含三个值,即 X、O 或 EMPTY。以下是我们留给你实现的功能!
|
让我们打开 `tictactoe.py` 来了解所提供的内容。首先,我们定义了三个变量:X、O 和 EMPTY,以表示游戏的可能移动。
|
||||||
|
|
||||||
|
函数 `initial_state` 返回游戏的启动状态。对于这个问题,我们选择将游戏状态表示为三个列表的列表(表示棋盘的三行),其中每个内部列表包含三个值,即 X、O 或 EMPTY。以下是我们留给你实现的功能!
|
||||||
|
|
||||||
## 说明
|
## 说明
|
||||||
|
|
||||||
- 实现 `player`, `actions`, `result`, `winner`, `terminal`, `utility`, 以及 `minimax`.
|
实现 `player`, `actions`, `result`, `winner`, `terminal`, `utility`, 以及 `minimax`.
|
||||||
|
|
||||||
- `player` 函数应该以棋盘状态作为输入,并返回轮到哪个玩家(X 或 O)。
|
- `player` 函数应该以棋盘状态作为输入,并返回轮到哪个玩家(X 或 O)。
|
||||||
|
|
||||||
- 在初始游戏状态下,X 获得第一步。随后,玩家交替进行每一个动作。
|
- 在初始游戏状态下,X 获得第一步。随后,玩家交替进行每一个动作。
|
||||||
- 如果提供结束棋盘状态作为输入(即游戏已经结束),则任何返回值都是可接受的。
|
- 如果提供结束棋盘状态作为输入(即游戏已经结束),则任何返回值都是可接受的。
|
||||||
- `actions` 函数应该返回一组在给定的棋盘状态上可以采取的所有可能的操作。
|
- `actions` 函数应该返回一组在给定的棋盘状态上可以采取的所有可能的操作。
|
||||||
|
|
||||||
- 每个动作都应该表示为元组 `(i,j)`,其中 `i` 对应于移动的行(0、1 或 2),`j` 对应于行中的哪个单元格对应于移动(也是 0、1、或 2)。
|
- 每个动作都应该表示为元组 `(i,j)`,其中 `i` 对应于移动的行(0、1 或 2),`j` 对应于行中的哪个单元格对应于移动(也是 0、1、或 2)。
|
||||||
- 可能的移动是棋盘上任何没有 X 或 O 的单元格。
|
- 可能的移动是棋盘上任何没有 X 或 O 的单元格。
|
||||||
- 如果提供结束棋盘状态作为输入,则任何返回值都是可接受的。
|
- 如果提供结束棋盘状态作为输入,则任何返回值都是可接受的。
|
||||||
- `result` 函数以一个棋盘状态和一个动作作为输入,并且应该返回一个新的棋盘状态,而不修改原始棋盘。
|
- `result` 函数以一个棋盘状态和一个动作作为输入,并且应该返回一个新的棋盘状态,而不修改原始棋盘。
|
||||||
|
|
||||||
- 如果 `action` 函数接受了一个无效的动作,你的程序应该<u>raise an exception</u>.
|
- 如果 `action` 函数接受了一个无效的动作,你的程序应该<u>raise an exception</u>.
|
||||||
- 返回的棋盘状态应该是从原始输入棋盘,并让轮到它的玩家在输入动作指示的单元格处移动所产生的棋盘。
|
- 返回的棋盘状态应该是从原始输入棋盘,并让轮到它的玩家在输入动作指示的单元格处移动所产生的棋盘。
|
||||||
- 重要的是,原始棋盘应该保持不变:因为 Minimax 最终需要在计算过程中考虑许多不同的棋盘状态。这意味着简单地更新棋盘上的单元格本身并不是 `result` 函数的正确实现。在做出任何更改之前,你可能需要先对棋盘状态进行<u>deep copy</u>。
|
- 重要的是,原始棋盘应该保持不变:因为 Minimax 最终需要在计算过程中考虑许多不同的棋盘状态。这意味着简单地更新棋盘上的单元格本身并不是 `result` 函数的正确实现。在做出任何更改之前,你可能需要先对棋盘状态进行<u>deep copy</u>。
|
||||||
- `winner` 函数应该接受一个棋盘作为输入,如果游戏结束,则返回游戏的获胜者。
|
- `winner` 函数应该接受一个棋盘作为输入,如果游戏结束,则返回游戏的获胜者。
|
||||||
|
|
||||||
- 如果 X 玩家赢得了游戏,函数应该返回 X。如果 O 玩家赢得了比赛,函数应该返回 O。
|
- 如果 X 玩家赢得了游戏,函数应该返回 X。如果 O 玩家赢得了比赛,函数应该返回 O。
|
||||||
- 一个人可以通过水平、垂直或对角连续三次移动赢得比赛。
|
- 一个人可以通过水平、垂直或对角连续三次移动赢得比赛。
|
||||||
- 你可以认为最多会有一个赢家(也就是说,没有一个棋盘会同时有两个玩家连着三个,因为这将是一个无效的棋盘状态)。
|
- 你可以认为最多会有一个赢家(也就是说,没有一个棋盘会同时有两个玩家连着三个,因为这将是一个无效的棋盘状态)。
|
||||||
- 如果游戏没有赢家(要么是因为游戏正在进行,要么是因为比赛以平局结束),函数应该返回 `None`。
|
- 如果游戏没有赢家(要么是因为游戏正在进行,要么是因为比赛以平局结束),函数应该返回 `None`。
|
||||||
- `terminal` 函数应该接受一个棋盘作为输入,并返回一个布尔值,指示游戏是否结束。
|
- `terminal` 函数应该接受一个棋盘作为输入,并返回一个布尔值,指示游戏是否结束。
|
||||||
|
|
||||||
- 如果游戏结束,要么是因为有人赢得了游戏,要么是由于所有单元格都已填充而没有人获胜,则函数应返回 `True`。
|
- 如果游戏结束,要么是因为有人赢得了游戏,要么是由于所有单元格都已填充而没有人获胜,则函数应返回 `True`。
|
||||||
- 否则,如果游戏仍在进行中,则函数应返回 `False`。
|
- 否则,如果游戏仍在进行中,则函数应返回 `False`。
|
||||||
- `utility` 函数应接受结束棋盘状态作为输入,并输出该棋盘的分数。
|
- `utility` 函数应接受结束棋盘状态作为输入,并输出该棋盘的分数。
|
||||||
|
|
||||||
- 如果 X 赢得了比赛,则分数为 1。如果 O 赢得了比赛,则分数为 -1。如果比赛以平局结束,则分数为 0。
|
- 如果 X 赢得了比赛,则分数为 1。如果 O 赢得了比赛,则分数为 -1。如果比赛以平局结束,则分数为 0。
|
||||||
- 你可以假设只有当 `terminal(board)` 为 True 时,才会在棋盘上调用 `utility`。
|
- 你可以假设只有当 `terminal(board)` 为 True 时,才会在棋盘上调用 `utility`。
|
||||||
- `minimax` 函数应该以一个棋盘作为输入,并返回玩家在该棋盘上移动的最佳移动。
|
- `minimax` 函数应该以一个棋盘作为输入,并返回玩家在该棋盘上移动的最佳移动。
|
||||||
|
|
||||||
- 返回的移动应该是最佳动作 `(i,j)`,这是棋盘上允许的动作之一。如果多次移动都是同样最佳的,那么这些移动中的任何一次都是可以接受的。
|
- 返回的移动应该是最佳动作 `(i,j)`,这是棋盘上允许的动作之一。如果多次移动都是同样最佳的,那么这些移动中的任何一次都是可以接受的。
|
||||||
- 如果该棋盘是结束棋盘状态,则 `minimax` 函数应返回 `None`。
|
- 如果该棋盘是结束棋盘状态,则 `minimax` 函数应返回 `None`。
|
||||||
- 对于所有接受棋盘作为输入的函数,你可以假设它是一个有效的棋盘(即,它是包含三行的列表,每行都有三个值 X、O 或 EMPTY)。你不应该修改所提供的函数声明(每个函数的参数的顺序或数量)。、
|
对于所有接受棋盘作为输入的函数,你可以假设它是一个有效的棋盘(即,它是包含三行的列表,每行都有三个值 X、O 或 EMPTY)。你不应该修改所提供的函数声明(每个函数的参数的顺序或数量)。、
|
||||||
- 一旦所有功能都得到了正确的实现,你就应该能够运行 `python runner.py` 并与你的人工智能进行比赛。而且,由于井字棋是双方最佳比赛的平局,你永远不应该能够击败人工智能(尽管如果你打得不好,它可能会打败你!)
|
一旦所有功能都得到了正确的实现,你就应该能够运行 `python runner.py` 并与你的人工智能进行比赛。而且,由于井字棋是双方最佳比赛的平局,你永远不应该能够击败人工智能(尽管如果你打得不好,它可能会打败你!)
|
||||||
|
|
||||||
## 提示
|
## 提示
|
||||||
|
|
||||||
|
|||||||
@@ -24,9 +24,12 @@
|
|||||||
|
|
||||||
在计算机科学中,还有许多其他形式的搜索问题,比如谜题或迷宫。
|
在计算机科学中,还有许多其他形式的搜索问题,比如谜题或迷宫。
|
||||||
|
|
||||||

|
<table>
|
||||||
|
<tr>
|
||||||

|
<td><img src=https://cdn.xyxsw.site/SYw4bOzqAo65PQxZQLucbZAxnHd.png width=520></td>
|
||||||
|
<td><img src=https://cdn.xyxsw.site/LPgEbVQg2oZBSexmGWwcwfbdnVd.png width=520></td>
|
||||||
|
</tr>
|
||||||
|
</table>
|
||||||
|
|
||||||
## 举个例子
|
## 举个例子
|
||||||
|
|
||||||
@@ -34,89 +37,100 @@
|
|||||||
|
|
||||||
- 智能主体 (Agent)
|
- 智能主体 (Agent)
|
||||||
|
|
||||||
- 感知其环境并对该环境采取行动的实体。
|
感知其环境并对该环境采取行动的实体。
|
||||||
- 例如,在导航应用程序中,智能主体将是一辆汽车的代表,它需要决定采取哪些行动才能到达目的地。
|
|
||||||
|
例如,在导航应用程序中,智能主体将是一辆汽车的代表,它需要决定采取哪些行动才能到达目的地。
|
||||||
|
|
||||||
- 状态 (State)
|
- 状态 (State)
|
||||||
|
|
||||||
- 智能主体在其环境中的配置。
|
智能主体在其环境中的配置。
|
||||||
- 例如,在一个数字华容道谜题中,一个状态是所有数字排列在棋盘上的任何一种方式。
|
|
||||||
|
例如,在一个数字华容道谜题中,一个状态是所有数字排列在棋盘上的任何一种方式。
|
||||||
|
|
||||||
- 初始状态(Initial State)
|
- 初始状态(Initial State)
|
||||||
|
|
||||||
- 搜索算法开始的状态。在导航应用程序中,这将是当前位置。
|
搜索算法开始的状态。在导航应用程序中,这将是当前位置。
|
||||||
|
|
||||||
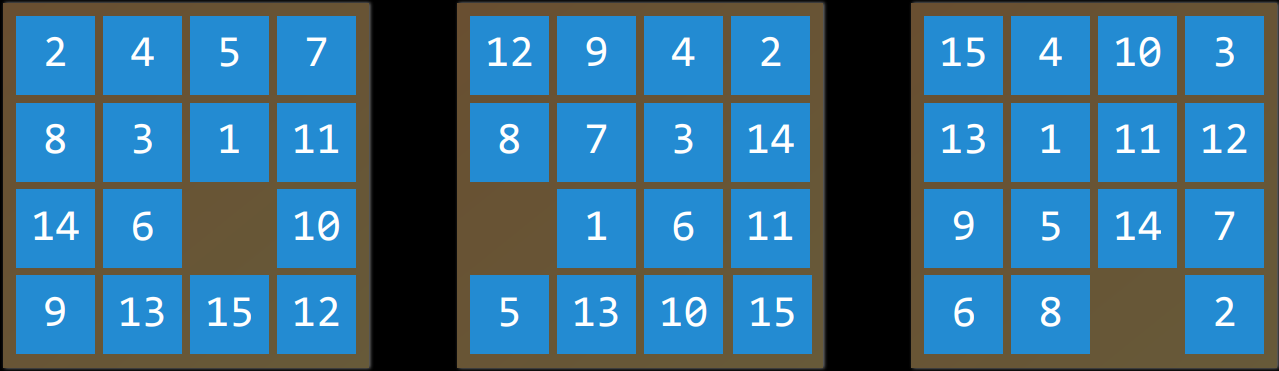
|

|
||||||
|
|
||||||
- 动作 (Action)
|
- 动作 (Action)
|
||||||
|
|
||||||
- 一个状态可以做出的选择。更确切地说,动作可以定义为一个函数。当接收到状态$s$作为输入时,$Actions(s)$将返回可在状态$s$ 中执行的一组操作作为输出。
|
一个状态可以做出的选择。更确切地说,动作可以定义为一个函数。当接收到状态$s$作为输入时,$Actions(s)$将返回可在状态$s$ 中执行的一组操作作为输出。
|
||||||
- 例如,在一个数字华容道中,给定状态的操作是您可以在当前配置中滑动方块的方式。
|
|
||||||
|
例如,在一个数字华容道中,给定状态的操作是您可以在当前配置中滑动方块的方式。
|
||||||
|
|
||||||
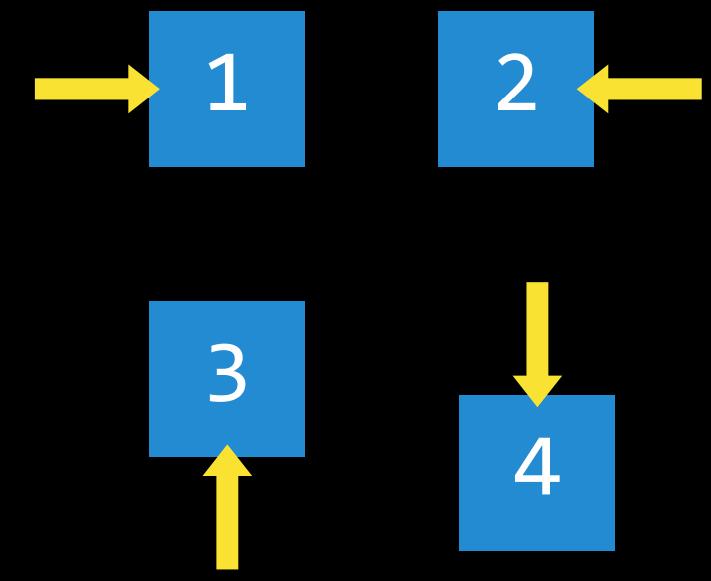
|

|
||||||
|
|
||||||
- 过渡模型 (Transition Model)
|
- 过渡模型 (Transition Model)
|
||||||
|
|
||||||
- 对在任何状态下执行任何适用操作所产生的状态的描述。
|
对在任何状态下执行任何适用操作所产生的状态的描述。
|
||||||
- 更确切地说,过渡模型可以定义为一个函数。
|
|
||||||
- 在接收到状态$s$和动作$a$作为输入时,$Results(s,a)$返回在状态$s$中执行动作$a$ 所产生的状态。
|
更确切地说,过渡模型可以定义为一个函数。
|
||||||
- 例如,给定数字华容道的特定配置(状态$s$),在任何方向上移动正方形(动作$a$)将导致谜题的新配置(新状态)。
|
|
||||||
|
在接收到状态$s$和动作$a$作为输入时,$Results(s,a)$返回在状态$s$中执行动作$a$ 所产生的状态。
|
||||||
|
|
||||||
|
例如,给定数字华容道的特定配置(状态$s$),在任何方向上移动正方形(动作$a$)将导致谜题的新配置(新状态)。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 状态空间 (State Space)
|
- 状态空间 (State Space)
|
||||||
|
|
||||||
- 通过一系列的操作目标从初始状态可达到的所有状态的集合。
|
通过一系列的操作目标从初始状态可达到的所有状态的集合。
|
||||||
- 例如,在一个数字华容道谜题中,状态空间由所有$\frac{16!}{2}$种配置,可以从任何初始状态达到。状态空间可以可视化为有向图,其中状态表示为节点,动作表示为节点之间的箭头。
|
|
||||||
|
例如,在一个数字华容道谜题中,状态空间由所有$\frac{16!}{2}$种配置,可以从任何初始状态达到。状态空间可以可视化为有向图,其中状态表示为节点,动作表示为节点之间的箭头。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 目标测试 (Goal Test)
|
- 目标测试 (Goal Test)
|
||||||
|
|
||||||
- 确定给定状态是否为目标状态的条件。例如,在导航应用程序中,目标测试将是智能主体的当前位置是否在目的地。如果是,问题解决了。如果不是,我们将继续搜索。
|
确定给定状态是否为目标状态的条件。例如,在导航应用程序中,目标测试将是智能主体的当前位置是否在目的地。如果是,问题解决了。如果不是,我们将继续搜索。
|
||||||
|
|
||||||
- 路径成本 (Path Cost)
|
- 路径成本 (Path Cost)
|
||||||
|
|
||||||
- 完成给定路径相关的代价。例如,导航应用程序并不是简单地让你达到目标;它这样做的同时最大限度地减少了路径成本,为您找到了达到目标状态的最快方法。
|
完成给定路径相关的代价。例如,导航应用程序并不是简单地让你达到目标;它这样做的同时最大限度地减少了路径成本,为您找到了达到目标状态的最快方法。
|
||||||
|
|
||||||
## 解决搜索问题
|
## 解决搜索问题
|
||||||
|
|
||||||
- 解 (solution)
|
### 解 (solution)
|
||||||
|
|
||||||
- 从初始状态到目标状态的一系列动作。
|
从初始状态到目标状态的一系列动作。
|
||||||
- 最优解 (Optimal Solution)
|
|
||||||
|
### 最优解 (Optimal Solution)
|
||||||
|
|
||||||
- 在所有解决方案中路径成本最低的解决方案。
|
- 在所有解决方案中路径成本最低的解决方案。
|
||||||
- 在搜索过程中,数据通常存储在**节点 (Node)** 中,节点是一种包含以下数据的数据结构:
|
- 在搜索过程中,数据通常存储在<strong>节点 (Node)</strong> 中,节点是一种包含以下数据的数据结构:
|
||||||
|
|
||||||
- 状态——state
|
- 状态——state
|
||||||
- 其父节点,通过该父节点生成当前节点——parent node
|
- 其父节点,通过该父节点生成当前节点——parent node
|
||||||
- 应用于父级状态以获取当前节点的操作——action
|
- 应用于父级状态以获取当前节点的操作——action
|
||||||
- 从初始状态到该节点的路径成本——path cost
|
- 从初始状态到该节点的路径成本——path cost
|
||||||
- 节点包含的信息使它们对于搜索算法非常有用。
|
- 节点包含的信息使它们对于搜索算法非常有用。
|
||||||
|
|
||||||
它们包含一个状态,可以使用目标测试来检查该状态是否为最终状态。
|
它们包含一个状态,可以使用目标测试来检查该状态是否为最终状态。
|
||||||
|
|
||||||
如果是,则可以将节点的路径成本与其他节点的路径代价进行比较,从而可以选择最佳解决方案。
|
如果是,则可以将节点的路径成本与其他节点的路径代价进行比较,从而可以选择最佳解决方案。
|
||||||
|
|
||||||
一旦选择了节点,通过存储父节点和从父节点到当前节点的动作,就可以追溯从初始状态到该节点的每一步,而这一系列动作就是解决方案。
|
一旦选择了节点,通过存储父节点和从父节点到当前节点的动作,就可以追溯从初始状态到该节点的每一步,而这一系列动作就是解决方案。
|
||||||
|
|
||||||
- 然而,节点只是一个数据结构——它们不搜索,而是保存信息。为了实际搜索,我们使用了边域 (frontier),即“管理”节点的机制。边域首先包含一个初始状态和一组空的已探索项目(探索集),然后重复以下操作,直到找到解决方案:
|
然而,节点只是一个数据结构——它们不搜索,而是保存信息。为了实际搜索,我们使用了边域 (frontier),即“管理”节点的机制。边域首先包含一个初始状态和一组空的已探索项目(探索集),然后重复以下操作,直到找到解决方案:
|
||||||
|
|
||||||
- 重复
|
重复:
|
||||||
|
|
||||||
- 如果边域为空
|
1. 如果边域为空
|
||||||
|
- 停止,搜索问题无解
|
||||||
|
2. 从边域中删除一个节点。这是将要考虑的节点。
|
||||||
|
3. 如果节点包含目标状态。
|
||||||
|
- 返回解决方案,停止
|
||||||
|
否则:
|
||||||
|
- 展开节点(找到可以从该节点到达的所有新节点),并将生成的节点添加到边域。
|
||||||
|
- 将当前节点添加到探索集。
|
||||||
|
|
||||||
- 停止,搜索问题无解
|
<table>
|
||||||
- 从边域中删除一个节点。这是将要考虑的节点。
|
<tr>
|
||||||
- 如果节点包含目标状态
|
<td><img src=https://cdn.xyxsw.site/K53FbGmswoM7JAxqJZxcQEjdnES.png width=520></td>
|
||||||
|
<td><img src=https://cdn.xyxsw.site/THhpbemEHoxl80xHeTjc9d35nVh.png width=520></td>
|
||||||
- 返回解决方案,停止
|
</tr>
|
||||||
- 否则
|
</table>
|
||||||
|
|
||||||
- 展开节点(找到可以从该节点到达的所有新节点),并将生成的节点添加到边域。
|
|
||||||
- 将当前节点添加到探索集。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
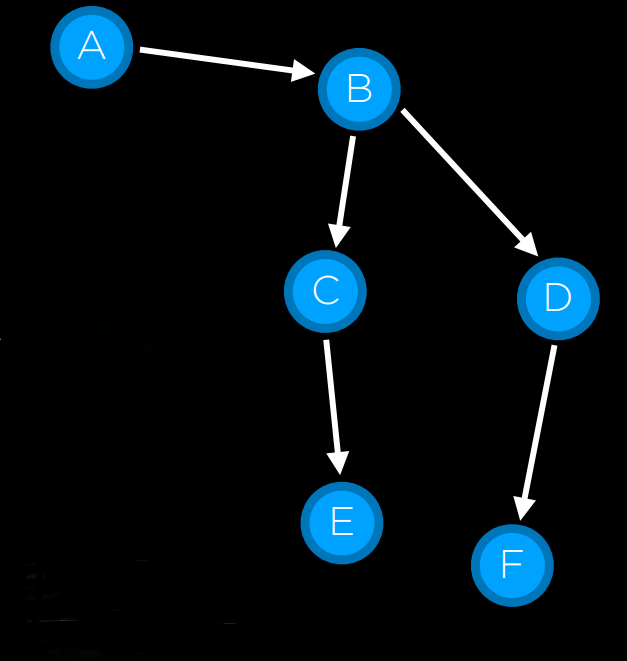
|
|
||||||
|
|
||||||
边域从节点 A 初始化开始
|
边域从节点 A 初始化开始
|
||||||
|
|
||||||
@@ -124,34 +138,44 @@
|
|||||||
2. 取出节点 B,展开,添加......
|
2. 取出节点 B,展开,添加......
|
||||||
3. 到达目标节点,停止,返回解决方案
|
3. 到达目标节点,停止,返回解决方案
|
||||||
|
|
||||||

|
<table>
|
||||||
|
<tr>
|
||||||
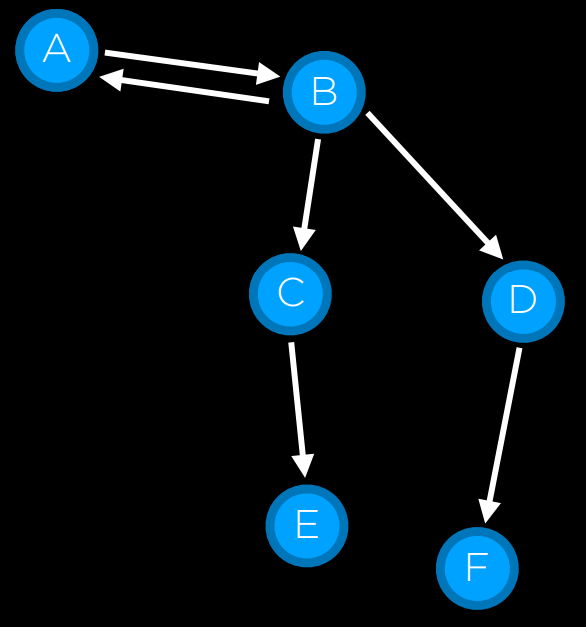
|
<td><img src=https://cdn.xyxsw.site/XmnObIGaUoF4ssxkgzUc4vTUnmf.png width=520></td>
|
||||||
|
<td><img src=https://cdn.xyxsw.site/Wsntb9rLwogdAKxpJgLchrI8nae.png width=520></td>
|
||||||
|
</tr>
|
||||||
|
</table>
|
||||||
|
|
||||||
会出现什么问题?节点 A-> 节点 B-> 节点 A->......-> 节点 A。我们需要一个探索集,记录已搜索的节点!
|
会出现什么问题?节点 A-> 节点 B-> 节点 A->......-> 节点 A。我们需要一个探索集,记录已搜索的节点!
|
||||||
|
|
||||||
### 不知情搜索 (Uninformed Search)
|
### 不知情搜索 (Uninformed Search)
|
||||||
|
|
||||||
- 在之前对边域的描述中,有一件事没有被提及。在上面伪代码的第 1 阶段,应该删除哪个节点?这种选择对解决方案的质量和实现速度有影响。关于应该首先考虑哪些节点的问题,有多种方法,其中两种可以用堆栈(深度优先搜索)和队列(广度优先搜索)的数据结构来表示。
|
在之前对边域的描述中,有一件事没有被提及。在上面伪代码的第 1 阶段,应该删除哪个节点?这种选择对解决方案的质量和实现速度有影响。关于应该首先考虑哪些节点的问题,有多种方法,其中两种可以用堆栈(深度优先搜索)和队列(广度优先搜索)的数据结构来表示。
|
||||||
- 深度优先搜索 (Depth-First Search)
|
|
||||||
|
|
||||||
- 深度优先搜索算法在尝试另一个方向之前耗尽每个方向。在这些情况下,边域作为堆栈数据结构进行管理。这里需要记住的流行语是“后进先出”。在将节点添加到边域后,第一个要删除和考虑的节点是最后一个要添加的节点。这导致了一种搜索算法,该算法在第一个方向上尽可能深入,直到尽头,同时将所有其他方向留到后面。“不撞南墙不回头”
|
#### 深度优先搜索 (Depth-First Search)
|
||||||
- (一个例子:以你正在寻找钥匙的情况为例。在深度优先搜索方法中,如果你选择从裤子里搜索开始,你会先仔细检查每一个口袋,清空每个口袋,仔细检查里面的东西。只有当你完全筋疲力尽时,你才会停止在裤子里搜索,开始在其他地方搜索。)
|
|
||||||
- 优点
|
|
||||||
|
|
||||||
- 在最好的情况下,这个算法是最快的。如果它“运气好”,并且总是(偶然)选择正确的解决方案路径,那么深度优先搜索需要尽可能少的时间来找到解决方案。
|
深度优先搜索算法在尝试另一个方向之前耗尽每个方向。在这些情况下,边域作为堆栈数据结构进行管理。这里需要记住的流行语是“后进先出”。在将节点添加到边域后,第一个要删除和考虑的节点是最后一个要添加的节点。这导致了一种搜索算法,该算法在第一个方向上尽可能深入,直到尽头,同时将所有其他方向留到后面。“不撞南墙不回头”
|
||||||
- 缺点
|
|
||||||
|
|
||||||
- 所找到的解决方案可能不是最优的。
|
(一个例子:以你正在寻找钥匙的情况为例。在深度优先搜索方法中,如果你选择从裤子里搜索开始,你会先仔细检查每一个口袋,清空每个口袋,仔细检查里面的东西。只有当你完全筋疲力尽时,你才会停止在裤子里搜索,开始在其他地方搜索。)
|
||||||
- 在最坏的情况下,该算法将在找到解决方案之前探索每一条可能的路径,从而在到达解决方案之前花费尽可能长的时间。
|
|
||||||
|
|
||||||
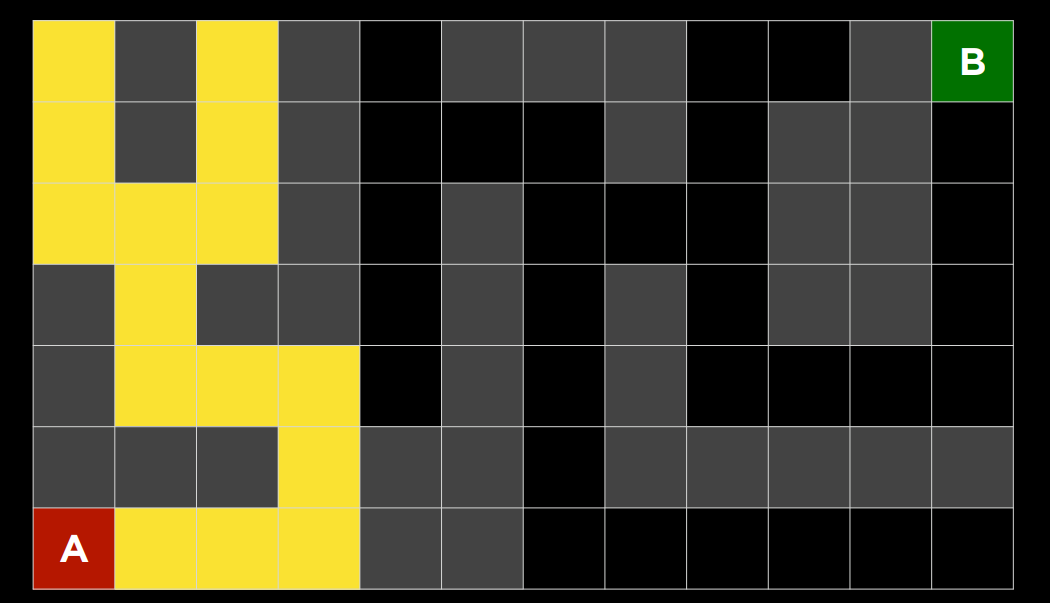
|
- 优点
|
||||||
|
- 在最好的情况下,这个算法是最快的。如果它“运气好”,并且总是(偶然)选择正确的解决方案路径,那么深度优先搜索需要尽可能少的时间来找到解决方案。
|
||||||
|
- 缺点
|
||||||
|
- 所找到的解决方案可能不是最优的。
|
||||||
|
- 在最坏的情况下,该算法将在找到解决方案之前探索每一条可能的路径,从而在到达解决方案之前花费尽可能长的时间。
|
||||||
|
|
||||||

|
<table>
|
||||||
|
<tr>
|
||||||
|
<td><img src=https://cdn.xyxsw.site/SGVWbCcTlobQwJxSjKvcNyJAnEG.png width=520></td>
|
||||||
|
<td><img src=https://cdn.xyxsw.site/Vv9Sb26QfoMrkqx5apycIYPJnlf.png width=520></td>
|
||||||
|
</tr>
|
||||||
|
</table>
|
||||||
|
|
||||||
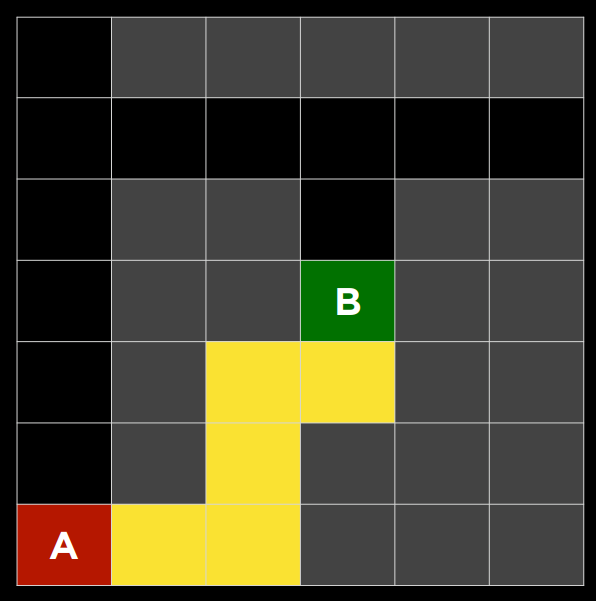
|
<table>
|
||||||
|
<tr>
|
||||||
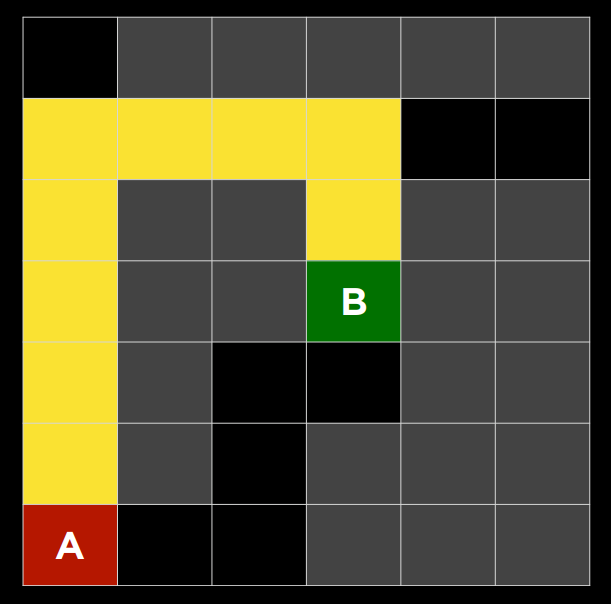
|
<td><img src=https://cdn.xyxsw.site/Gjd5bpdpcoIxGtxcUJ0c2OVfnOf.png width=520></td>
|
||||||
|
<td><img src=https://cdn.xyxsw.site/M2vZbA5hpoT9RExuAGwcBHF1nmh.png width=520></td>
|
||||||
|
</tr>
|
||||||
|
</table>
|
||||||
|
|
||||||
- 代码实现
|
- 代码实现
|
||||||
|
|
||||||
@@ -165,27 +189,33 @@ def remove(self):
|
|||||||
return node
|
return node
|
||||||
```
|
```
|
||||||
|
|
||||||
- 广度优先搜索 (Breadth-First Search)
|
#### 广度优先搜索 (Breadth-First Search)
|
||||||
|
|
||||||
- 广度优先搜索算法将同时遵循多个方向,在每个可能的方向上迈出一步,然后在每个方向上迈出第二步。在这种情况下,边域作为队列数据结构进行管理。这里需要记住的流行语是“先进先出”。在这种情况下,所有新节点都会排成一行,并根据先添加的节点来考虑节点(先到先得!)。这导致搜索算法在任何一个方向上迈出第二步之前,在每个可能的方向上迈出一步。
|
广度优先搜索算法将同时遵循多个方向,在每个可能的方向上迈出一步,然后在每个方向上迈出第二步。在这种情况下,边域作为队列数据结构进行管理。这里需要记住的流行语是“先进先出”。在这种情况下,所有新节点都会排成一行,并根据先添加的节点来考虑节点(先到先得!)。这导致搜索算法在任何一个方向上迈出第二步之前,在每个可能的方向上迈出一步。
|
||||||
- (一个例子:假设你正在寻找钥匙。在这种情况下,如果你从裤子开始,你会看你的右口袋。之后,你会在一个抽屉里看一眼,而不是看你的左口袋。然后在桌子上。以此类推,在你能想到的每个地方。只有在你用完所有位置后,你才会回到你的裤子上,在下一个口袋里找。)
|
|
||||||
- 优点
|
|
||||||
|
|
||||||
- 该算法可以保证找到最优解。
|
(一个例子:假设你正在寻找钥匙。在这种情况下,如果你从裤子开始,你会看你的右口袋。之后,你会在一个抽屉里看一眼,而不是看你的左口袋。然后在桌子上。以此类推,在你能想到的每个地方。只有在你用完所有位置后,你才会回到你的裤子上,在下一个口袋里找。)
|
||||||
- 缺点
|
|
||||||
|
|
||||||
- 几乎可以保证该算法的运行时间会比最短时间更长。
|
- 优点
|
||||||
- 在最坏的情况下,这种算法需要尽可能长的时间才能运行。
|
- 该算法可以保证找到最优解。
|
||||||
|
- 缺点
|
||||||
|
- 几乎可以保证该算法的运行时间会比最短时间更长。
|
||||||
|
- 在最坏的情况下,这种算法需要尽可能长的时间才能运行。
|
||||||
|
|
||||||

|
<table>
|
||||||
|
<tr>
|
||||||
|
<td><img src=https://cdn.xyxsw.site/S6SRbMUrcoYQCYxZGgJczkdcnBP.png width=520></td>
|
||||||
|
<td><img src=https://cdn.xyxsw.site/Xg7Qbv59IoQB3bxPFO1ceXgRnkf.png width=520></td>
|
||||||
|
</tr>
|
||||||
|
</table>
|
||||||
|
|
||||||
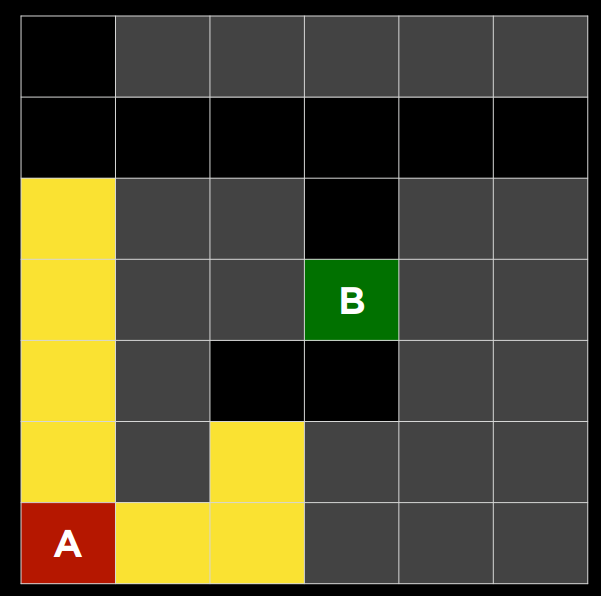
|
<table>
|
||||||
|
<tr>
|
||||||
|
<td><img src=https://cdn.xyxsw.site/X34Rb5R7AonUg3xYs7DcQzSfndg.png width=520></td>
|
||||||
|
<td><img src=https://cdn.xyxsw.site/PQeZbJv3Bom6NYxa6lccT084nFn.png width=520></td>
|
||||||
|
</tr>
|
||||||
|
</table>
|
||||||
|
|
||||||
|
代码实现
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
- 代码实现
|
|
||||||
|
|
||||||
```python
|
```python
|
||||||
def remove(self):
|
def remove(self):
|
||||||
@@ -199,74 +229,81 @@ def remove(self):
|
|||||||
|
|
||||||
## 知情搜索 (Informed Search)
|
## 知情搜索 (Informed Search)
|
||||||
|
|
||||||
- 广度优先和深度优先都是不知情的搜索算法。也就是说,这些算法没有利用他们没有通过自己的探索获得的关于问题的任何知识。然而,大多数情况下,关于这个问题的一些知识实际上是可用的。例如,当人类进入一个路口时,人类可以看到哪条路沿着解决方案的大致方向前进,哪条路没有。人工智能也可以这样做。一种考虑额外知识以试图提高性能的算法被称为知情搜索算法。
|
广度优先和深度优先都是不知情的搜索算法。也就是说,这些算法没有利用他们没有通过自己的探索获得的关于问题的任何知识。然而,大多数情况下,关于这个问题的一些知识实际上是可用的。例如,当人类进入一个路口时,人类可以看到哪条路沿着解决方案的大致方向前进,哪条路没有。人工智能也可以这样做。一种考虑额外知识以试图提高性能的算法被称为知情搜索算法。
|
||||||
- 贪婪最佳优先搜索 (Greedy Best-First Search)
|
|
||||||
|
### 贪婪最佳优先搜索 (Greedy Best-First Search)
|
||||||
|
|
||||||
|
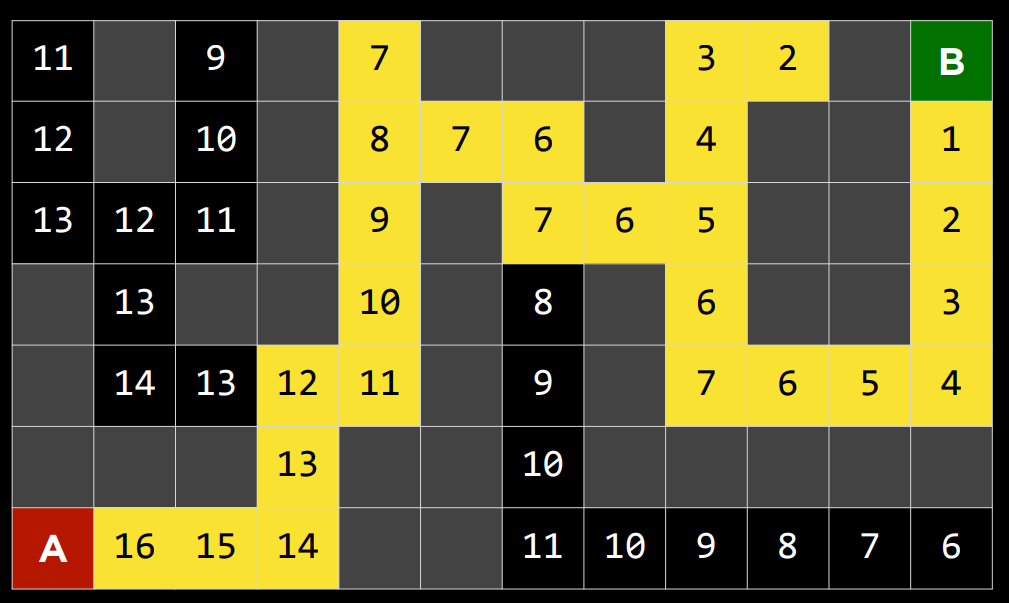
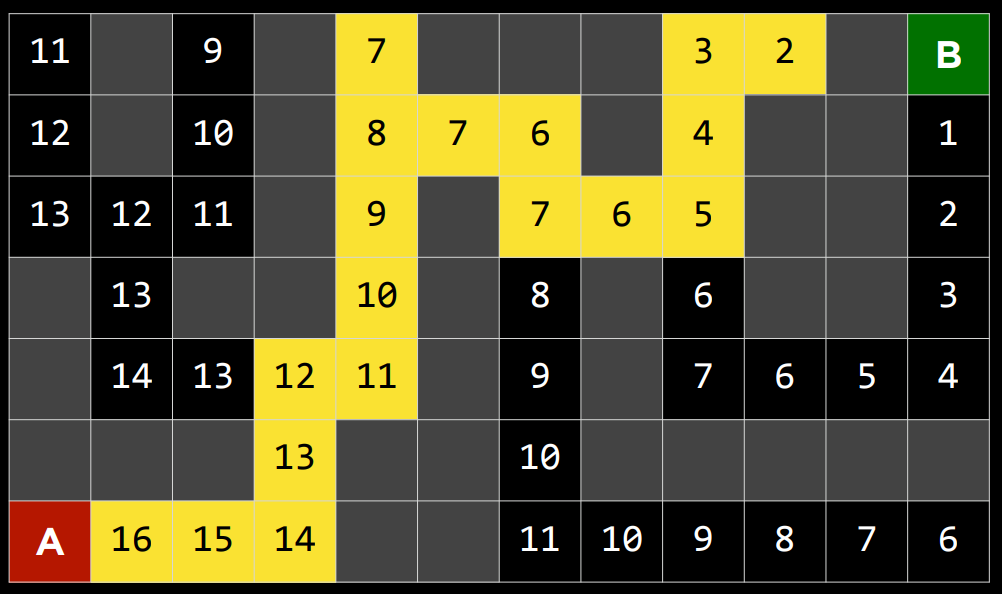
贪婪最佳优先搜索扩展最接近目标的节点,如启发式函数$h(n)$所确定的。顾名思义,该函数估计下一个节点离目标有多近,但可能会出错。贪婪最佳优先算法的效率取决于启发式函数的好坏。例如,在迷宫中,算法可以使用启发式函数,该函数依赖于可能节点和迷宫末端之间的曼哈顿距离。曼哈顿距离忽略了墙壁,并计算了从一个位置到目标位置需要向上、向下或向两侧走多少步。这是一个简单的估计,可以基于当前位置和目标位置的$(x,y)$坐标导出。
|
||||||
|
|
||||||
- 贪婪最佳优先搜索扩展最接近目标的节点,如启发式函数$h(n)$所确定的。顾名思义,该函数估计下一个节点离目标有多近,但可能会出错。贪婪最佳优先算法的效率取决于启发式函数的好坏。例如,在迷宫中,算法可以使用启发式函数,该函数依赖于可能节点和迷宫末端之间的曼哈顿距离。曼哈顿距离忽略了墙壁,并计算了从一个位置到目标位置需要向上、向下或向两侧走多少步。这是一个简单的估计,可以基于当前位置和目标位置的$(x,y)$坐标导出。
|
|
||||||
|

|
||||||
|
|
||||||
- 然而,重要的是要强调,与任何启发式算法一样,它可能会出错,并导致算法走上比其他情况下更慢的道路。不知情的搜索算法有可能更快地提供一个更好的解决方案,但它比知情算法更不可能这样。
|
然而,重要的是要强调,与任何启发式算法一样,它可能会出错,并导致算法走上比其他情况下更慢的道路。不知情的搜索算法有可能更快地提供一个更好的解决方案,但它比知情算法更不可能这样。
|
||||||
|
|
||||||
|
<table>
|
||||||
|
<tr>
|
||||||
|
<td><img src=https://cdn.xyxsw.site/SU2DbQeN2oxs5ex3K3NcMaJfnch.png width=520></td>
|
||||||
|
<td><img src=https://cdn.xyxsw.site/HkvdbcEdmo6RtjxOqqic31XFnSh.png width=520></td>
|
||||||
|
</tr>
|
||||||
|
</table>
|
||||||
|
|
||||||
|
### $A^*$搜索
|
||||||
|
|
||||||
- $A^*$搜索
|
作为贪婪最佳优先算法的一种发展,$A^{*}$ 搜索不仅考虑了从当前位置到目标的估计成本 $h(n)$ ,还考虑了直到当前位置为止累积的成本 $g(n)$ 。通过组合这两个值,该算法可以更准确地确定解决方案的成本并在旅途中优化其选择。该算法跟踪(到目前为止的路径成本 + 到目标的估计成本, $g(n)+h(n)$ ),一旦它超过了之前某个选项的估计成本,该算法将放弃当前路径并返回到之前的选项,从而防止自己沿着 $h(n)$ 错误地标记为最佳的却长而低效的路径前进。
|
||||||
|
|
||||||
- 作为贪婪最佳优先算法的一种发展,$A^*$搜索不仅考虑了从当前位置到目标的估计成本$h(n)$,还考虑了直到当前位置为止累积的成本$g(n)$。通过组合这两个值,该算法可以更准确地确定解决方案的成本并在旅途中优化其选择。该算法跟踪(到目前为止的路径成本 + 到目标的估计成本,$g(n)+h(n)$),一旦它超过了之前某个选项的估计成本,该算法将放弃当前路径并返回到之前的选项,从而防止自己沿着$h(n)$错误地标记为最佳的却长而低效的路径前进。
|
然而,由于这种算法也依赖于启发式,所以它依赖它所使用的启发式。在某些情况下,它可能比贪婪的最佳第一搜索甚至不知情的算法效率更低。对于最佳的$A^*$搜索,启发式函数$h(n)$应该:
|
||||||
|
|
||||||
- 然而,由于这种算法也依赖于启发式,所以它依赖它所使用的启发式。在某些情况下,它可能比贪婪的最佳第一搜索甚至不知情的算法效率更低。对于最佳的$A^*$搜索,启发式函数$h(n)$应该:
|
- 可接受,从未高估真实成本。
|
||||||
|
- 一致性,这意味着从新节点到目标的估计路径成本加上从先前节点转换到该新节点的成本应该大于或等于先前节点到目标的估计路径成本。用方程的形式表示,$h(n)$是一致的,如果对于每个节点 n$和后续节点 n'$,从 n$到$n'$的步长为 c$,满足$h(n) ≤ h(n') + c$.
|
||||||
|
|
||||||
- 可接受,从未高估真实成本。
|
<table>
|
||||||
|
<tr>
|
||||||
- 一致性,这意味着从新节点到目标的估计路径成本加上从先前节点转换到该新节点的成本应该大于或等于先前节点到目标的估计路径成本。用方程的形式表示,$h(n)$是一致的,如果对于每个节点 n$和后续节点 n'$,从 n$到$n'$的步长为 c$,满足$h(n) ≤ h(n') + c$.
|
<td><img src=https://cdn.xyxsw.site/BbIiba1pwo3uI7x4k7QcwicznGc.png width=520></td>
|
||||||
|
<td><img src=https://cdn.xyxsw.site/HhG9bcJP2okKMMxY0FGclP0AnXY.png width=520></td>
|
||||||

|
</tr>
|
||||||
|
</table>
|
||||||
|
|
||||||
|
|
||||||
## 对抗性搜索
|
## 对抗性搜索
|
||||||
|
|
||||||
尽管之前我们讨论过需要找到问题答案的算法,但在对抗性搜索中,算法面对的是试图实现相反目标的对手。通常,在游戏中会遇到使用对抗性搜索的人工智能,比如井字游戏。
|
尽管之前我们讨论过需要找到问题答案的算法,但在对抗性搜索中,算法面对的是试图实现相反目标的对手。通常,在游戏中会遇到使用对抗性搜索的人工智能,比如井字游戏。
|
||||||
|
|
||||||
- 极大极小算法 (Minimax)
|
### 极大极小算法 (Minimax)
|
||||||
|
|
||||||
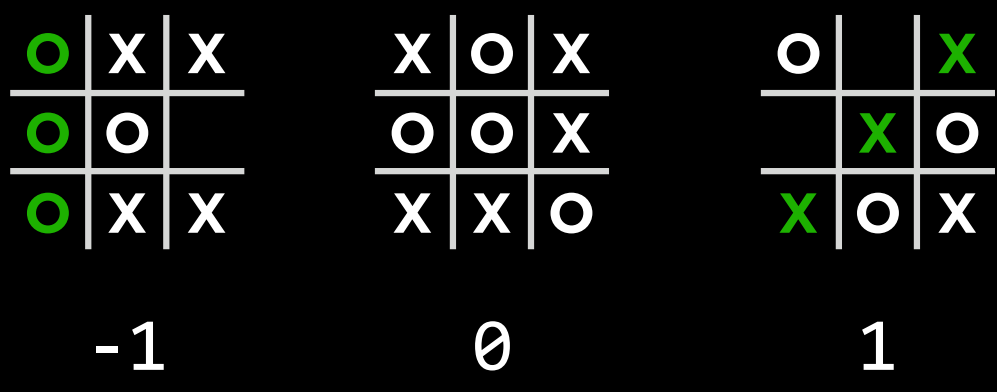
- 作为对抗性搜索中的一种算法,Minimax 将获胜条件表示为$(-1)$表示为一方,$(+1)$表示为另一方。进一步的行动将受到这些条件的驱动,最小化的一方试图获得最低分数,而最大化的一方则试图获得最高分数。
|
- 作为对抗性搜索中的一种算法,Minimax 将获胜条件表示为$(-1)$表示为一方,$(+1)$表示为另一方。进一步的行动将受到这些条件的驱动,最小化的一方试图获得最低分数,而最大化的一方则试图获得最高分数。
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
- 井字棋 AI 为例
|
#### 井字棋 AI 为例
|
||||||
|
|
||||||
- $s_0$: 初始状态(在我们的情况下,是一个空的 3X3 棋盘)
|
- $s_0$: 初始状态(在我们的情况下,是一个空的 3X3 棋盘)
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
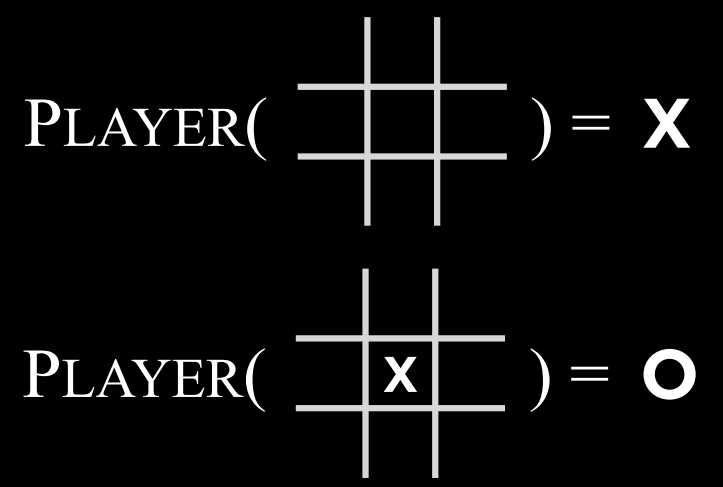
- $Players(s)$: 一个函数,在给定状态$$s$$的情况下,返回轮到哪个玩家(X 或 O)。
|
- $Players(s)$: 一个函数,在给定状态$s$的情况下,返回轮到哪个玩家(X 或 O)。
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
- $Actions(s)$: 一个函数,在给定状态$$s$$的情况下,返回该状态下的所有合法动作(棋盘上哪些位置是空的)。
|
- $Actions(s)$: 一个函数,在给定状态$s$的情况下,返回该状态下的所有合法动作(棋盘上哪些位置是空的)。
|
||||||
|
|
||||||
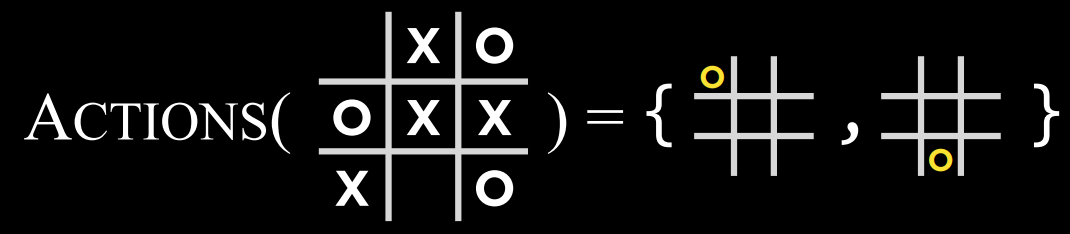
|
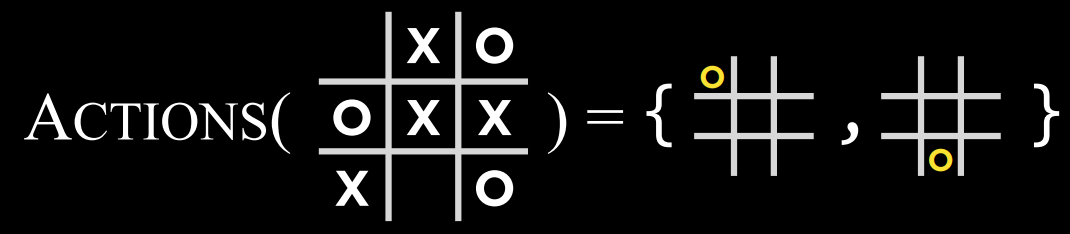
|
||||||
|
|
||||||
- $Result(s, a)$: 一个函数,在给定状态$$s$$和操作$$a$$的情况下,返回一个新状态。这是在状态$$s$$上执行动作$$a$$(在游戏中移动)所产生的棋盘。
|
- $Result(s, a)$: 一个函数,在给定状态$s$和操作$a$的情况下,返回一个新状态。这是在状态$s$上执行动作$a$(在游戏中移动)所产生的棋盘。
|
||||||
|
|
||||||
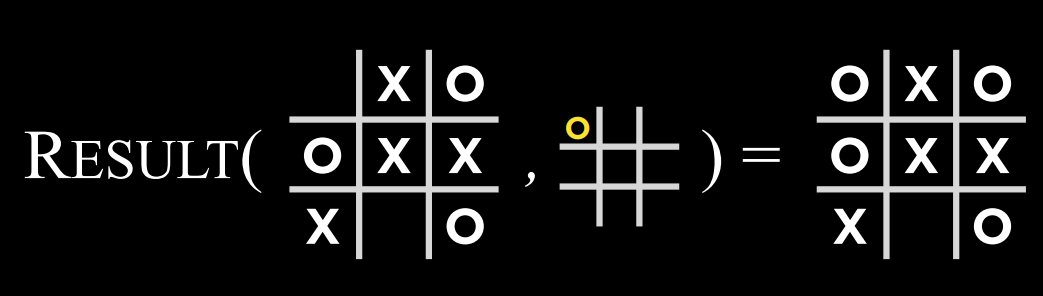
|
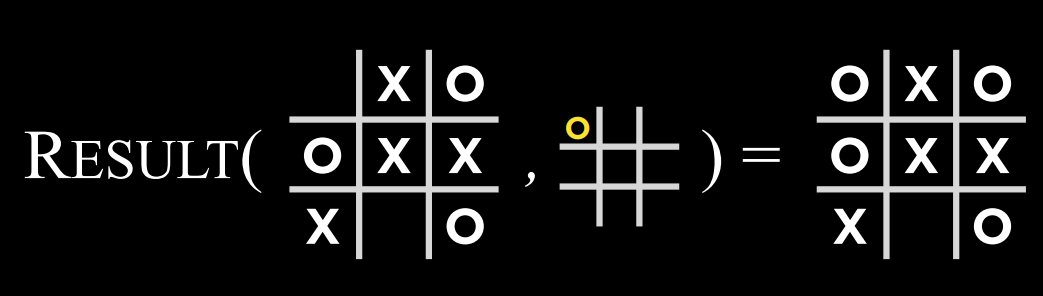
|
||||||
|
|
||||||
- $Terminal(s)$: 一个函数,在给定状态$$s$$的情况下,检查这是否是游戏的最后一步,即是否有人赢了或打成平手。如果游戏已结束,则返回 True,否则返回 False。
|
- $Terminal(s)$: 一个函数,在给定状态$s$的情况下,检查这是否是游戏的最后一步,即是否有人赢了或打成平手。如果游戏已结束,则返回 True,否则返回 False。
|
||||||
|
|
||||||
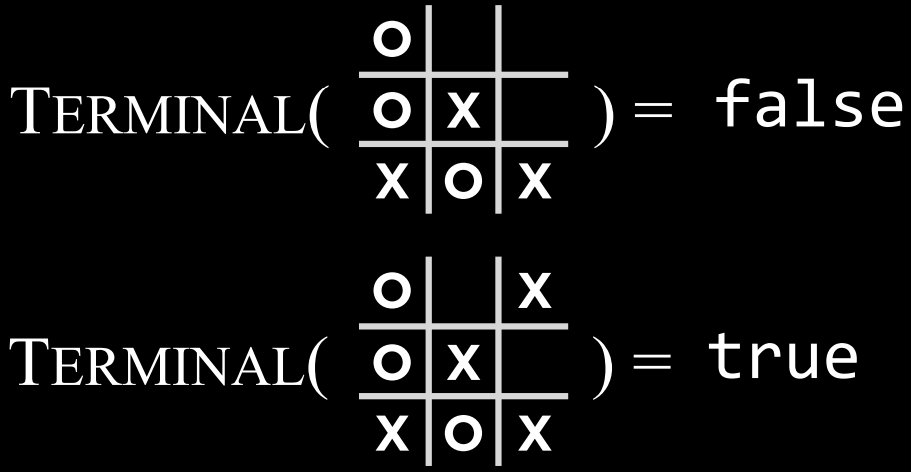
|
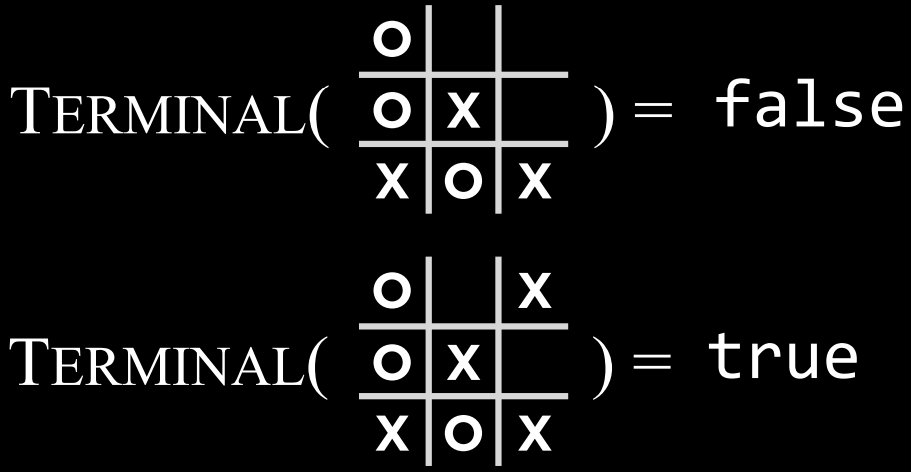
|
||||||
|
|
||||||
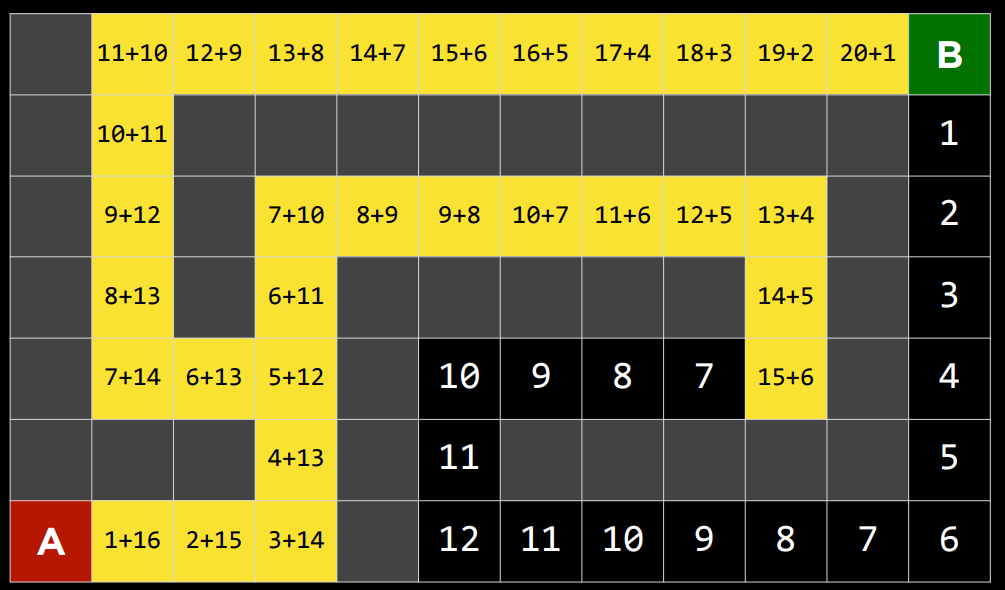
- $Utility(s)$: 一个函数,在给定终端状态 s 的情况下,返回状态的效用值:$$-1、0 或 1$$。
|
- $Utility(s)$: 一个函数,在给定终端状态 s 的情况下,返回状态的效用值:$-1、0 或 1$。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 算法的工作原理:
|
算法的工作原理:
|
||||||
|
|
||||||
- 该算法递归地模拟从当前状态开始直到达到终端状态为止可能发生的所有游戏状态。每个终端状态的值为$(-1)$、$0$或$(+1)$。
|
- 该算法递归地模拟从当前状态开始直到达到终端状态为止可能发生的所有游戏状态。每个终端状态的值为$(-1)$、$0$或$(+1)$。
|
||||||

|

|
||||||
|
|
||||||
- 根据轮到谁的状态,算法可以知道当前玩家在最佳游戏时是否会选择导致状态值更低或更高的动作。
|
- 根据轮到谁的状态,算法可以知道当前玩家在最佳游戏时是否会选择导致状态值更低或更高的动作。
|
||||||
|
|
||||||
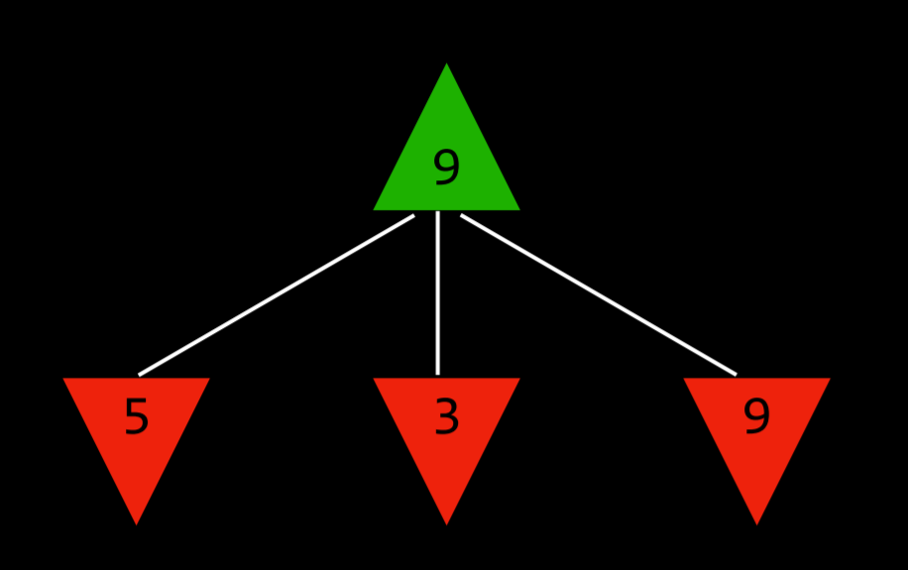
通过这种方式,在最小化和最大化之间交替,算法为每个可能的动作产生的状态创建值。举一个更具体的例子,我们可以想象,最大化的玩家在每一个回合都会问:“如果我采取这个行动,就会产生一个新的状态。如果最小化的玩家发挥得最好,那么该玩家可以采取什么行动来达到最低值?”
|
通过这种方式,在最小化和最大化之间交替,算法为每个可能的动作产生的状态创建值。举一个更具体的例子,我们可以想象,最大化的玩家在每一个回合都会问:“如果我采取这个行动,就会产生一个新的状态。如果最小化的玩家发挥得最好,那么该玩家可以采取什么行动来达到最低值?”
|
||||||
|
|
||||||
@@ -278,12 +315,11 @@ def remove(self):
|
|||||||
|
|
||||||
|

|
||||||
|
|
||||||
- 具体算法:
|
具体算法:
|
||||||
|
|
||||||
- 给定状态 $s$
|
- 给定状态 $s$
|
||||||
|
- 最大化玩家在$Actions(s)$中选择动作$a$,该动作产生$Min-value(Result(s,a))$ 的最高值。
|
||||||
- 最大化玩家在$Actions(s)$中选择动作$a$,该动作产生$Min-value(Result(s,a))$ 的最高值。
|
- 最小化玩家在$Actions(s)$中选择动作$a$,该动作产生$Max-value(Result(s,a))$ 的最小值。
|
||||||
- 最小化玩家在$Actions(s)$中选择动作$a$,该动作产生$Max-value(Result(s,a))$ 的最小值。
|
|
||||||
|
|
||||||
```txt
|
```txt
|
||||||
Function Max-Value(state):
|
Function Max-Value(state):
|
||||||
@@ -304,16 +340,16 @@ def remove(self):
|
|||||||
|
|
||||||
不会理解递归?也许你需要看看这个:[阶段二:递归操作](../3.%E7%BC%96%E7%A8%8B%E6%80%9D%E7%BB%B4%E4%BD%93%E7%B3%BB%E6%9E%84%E5%BB%BA/3.6.4.2%E9%98%B6%E6%AE%B5%E4%BA%8C%EF%BC%9A%E9%80%92%E5%BD%92%E6%93%8D%E4%BD%9C.md)
|
不会理解递归?也许你需要看看这个:[阶段二:递归操作](../3.%E7%BC%96%E7%A8%8B%E6%80%9D%E7%BB%B4%E4%BD%93%E7%B3%BB%E6%9E%84%E5%BB%BA/3.6.4.2%E9%98%B6%E6%AE%B5%E4%BA%8C%EF%BC%9A%E9%80%92%E5%BD%92%E6%93%8D%E4%BD%9C.md)
|
||||||
|
|
||||||
- $\alpha$-$\beta$剪枝 (Alpha-Beta Pruning)
|
### $\alpha$-$\beta$剪枝 (Alpha-Beta Pruning)
|
||||||
|
|
||||||
- 作为一种优化 Minimax 的方法,Alpha-Beta 剪枝跳过了一些明显不利的递归计算。在确定了一个动作的价值后,如果有初步证据表明接下来的动作可以让对手获得比已经确定的动作更好的分数,那么就没有必要进一步调查这个动作,因为它肯定比之前确定的动作不利。
|
作为一种优化 Minimax 的方法,Alpha-Beta 剪枝跳过了一些明显不利的递归计算。在确定了一个动作的价值后,如果有初步证据表明接下来的动作可以让对手获得比已经确定的动作更好的分数,那么就没有必要进一步调查这个动作,因为它肯定比之前确定的动作不利。
|
||||||
|
|
||||||
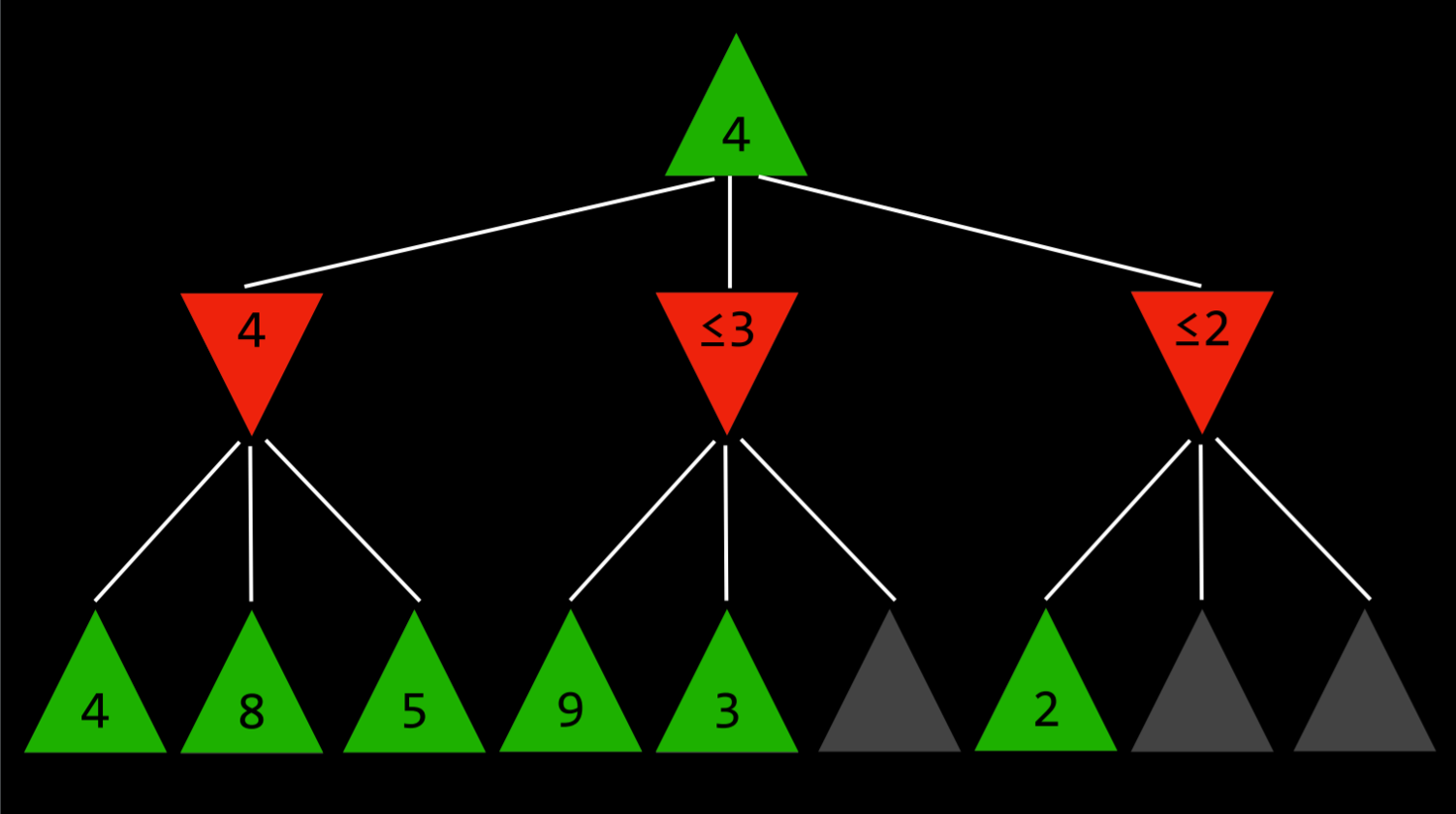
- 这一点最容易用一个例子来说明:最大化的玩家知道,在下一步,最小化的玩家将试图获得最低分数。假设最大化玩家有三个可能的动作,第一个动作的值为 4。然后玩家开始为下一个动作生成值。要做到这一点,如果当前玩家做出这个动作,玩家会生成最小化者动作的值,并且知道最小化者会选择最低的一个。然而,在完成最小化器所有可能动作的计算之前,玩家会看到其中一个选项的值为 3。这意味着没有理由继续探索最小化玩家的其他可能行动。尚未赋值的动作的值无关紧要,无论是 10 还是(-10)。如果该值为 10,则最小化器将选择最低选项 3,该选项已经比预先设定的 4 差。如果尚未估价的行动结果是(-10),那么最小化者将选择(-10)这一选项,这对最大化者来说更加不利。因此,在这一点上为最小化者计算额外的可能动作与最大化者无关,因为最大化玩家已经有了一个明确的更好的选择,其值为 4。
|
这一点最容易用一个例子来说明:最大化的玩家知道,在下一步,最小化的玩家将试图获得最低分数。假设最大化玩家有三个可能的动作,第一个动作的值为 4。然后玩家开始为下一个动作生成值。要做到这一点,如果当前玩家做出这个动作,玩家会生成最小化者动作的值,并且知道最小化者会选择最低的一个。然而,在完成最小化器所有可能动作的计算之前,玩家会看到其中一个选项的值为 3。这意味着没有理由继续探索最小化玩家的其他可能行动。尚未赋值的动作的值无关紧要,无论是 10 还是(-10)。如果该值为 10,则最小化器将选择最低选项 3,该选项已经比预先设定的 4 差。如果尚未估价的行动结果是(-10),那么最小化者将选择(-10)这一选项,这对最大化者来说更加不利。因此,在这一点上为最小化者计算额外的可能动作与最大化者无关,因为最大化玩家已经有了一个明确的更好的选择,其值为 4。
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
- 深度限制的极大极小算法 (Depth-Limited Minimax)
|
### 深度限制的极大极小算法 (Depth-Limited Minimax)
|
||||||
|
|
||||||
- 总共有$255168$个可能的井字棋游戏,以及有$10^{29000}$个可能的国际象棋中游戏。到目前为止,最小最大算法需要生成从某个点到**终端条件**的所有假设游戏状态。虽然计算所有的井字棋游戏状态对现代计算机来说并不是一个挑战,但目前用来计算国际象棋是不可能的。
|
- 总共有$255168$个可能的井字棋游戏,以及有$10^{29000}$个可能的国际象棋中游戏。到目前为止,最小最大算法需要生成从某个点到<strong>终端条件</strong>的所有假设游戏状态。虽然计算所有的井字棋游戏状态对现代计算机来说并不是一个挑战,但目前用来计算国际象棋是不可能的。
|
||||||
|
|
||||||
- 深度限制的 Minimax 算法在停止之前只考虑预先定义的移动次数,而从未达到终端状态。然而,这不允许获得每个动作的精确值,因为假设的游戏还没有结束。为了解决这个问题,深度限制 Minimax 依赖于一个评估函数,该函数从给定状态估计游戏的预期效用,或者换句话说,为状态赋值。例如,在国际象棋游戏中,效用函数会将棋盘的当前配置作为输入,尝试评估其预期效用(基于每个玩家拥有的棋子及其在棋盘上的位置),然后返回一个正值或负值,表示棋盘对一个玩家对另一个玩家的有利程度。这些值可以用来决定正确的操作,并且评估函数越好,依赖它的 Minimax 算法就越好。
|
深度限制的 Minimax 算法在停止之前只考虑预先定义的移动次数,而从未达到终端状态。然而,这不允许获得每个动作的精确值,因为假设的游戏还没有结束。为了解决这个问题,深度限制 Minimax 依赖于一个评估函数,该函数从给定状态估计游戏的预期效用,或者换句话说,为状态赋值。例如,在国际象棋游戏中,效用函数会将棋盘的当前配置作为输入,尝试评估其预期效用(基于每个玩家拥有的棋子及其在棋盘上的位置),然后返回一个正值或负值,表示棋盘对一个玩家对另一个玩家的有利程度。这些值可以用来决定正确的操作,并且评估函数越好,依赖它的 Minimax 算法就越好。
|
||||||
|
|||||||
@@ -15,62 +15,75 @@
|
|||||||
|
|
||||||
### 背景
|
### 背景
|
||||||
|
|
||||||
- 在 1978 年,逻辑学家雷蒙德·斯穆里安(Raymond Smullyan)出版了《这本书叫什么名字?》,这是一本逻辑难题的书。在书中的谜题中,有一类谜题被斯穆里安称为“骑士与流氓”谜题。
|
在 1978 年,逻辑学家雷蒙德·斯穆里安(Raymond Smullyan)出版了《这本书叫什么名字?》,这是一本逻辑难题的书。在书中的谜题中,有一类谜题被斯穆里安称为“骑士与流氓”谜题。
|
||||||
- 在骑士与流氓谜题中,给出了以下信息:每个角色要么是骑士,要么是流氓。骑士总是会说实话:如果骑士陈述了一句话,那么这句话就是真的。相反,流氓总是说谎:如果流氓陈述了一个句子,那么这个句子就是假的。
|
|
||||||
- 谜题的目标是,给出每个角色说的一组句子,确定每个角色是骑士还是流氓。
|
在骑士与流氓谜题中,给出了以下信息:每个角色要么是骑士,要么是流氓。骑士总是会说实话:如果骑士陈述了一句话,那么这句话就是真的。相反,流氓总是说谎:如果流氓陈述了一个句子,那么这个句子就是假的。
|
||||||
- 比如,这里有一个简单的谜题只有一个名为 A 的角色。A 说:“我既是骑士又是流氓。”
|
|
||||||
- 从逻辑上讲,我们可以推断,如果 A 是骑士,那么这句话一定是真的。但我们知道这句话不可能是真的,因为 A 不可能既是骑士又是流氓——我们知道每个角色要么是骑士,要么是流氓,不会出现是流氓的骑士或是骑士的流氓。所以,我们可以得出结论,A 一定是流氓。
|
谜题的目标是,给出每个角色说的一组句子,确定每个角色是骑士还是流氓。
|
||||||
- 那个谜题比较简单。随着更多的字符和更多的句子,谜题可以变得更加棘手!你在这个问题中的任务是确定如何使用命题逻辑来表示这些谜题,这样一个运行模型检查算法的人工智能可以为我们解决这些谜题。
|
|
||||||
|
比如,这里有一个简单的谜题只有一个名为 A 的角色。A 说:“我既是骑士又是流氓。”
|
||||||
|
|
||||||
|
从逻辑上讲,我们可以推断,如果 A 是骑士,那么这句话一定是真的。但我们知道这句话不可能是真的,因为 A 不可能既是骑士又是流氓——我们知道每个角色要么是骑士,要么是流氓,不会出现是流氓的骑士或是骑士的流氓。所以,我们可以得出结论,A 一定是流氓。
|
||||||
|
|
||||||
|
那个谜题比较简单。随着更多的字符和更多的句子,谜题可以变得更加棘手!你在这个问题中的任务是确定如何使用命题逻辑来表示这些谜题,这样一个运行模型检查算法的人工智能可以为我们解决这些谜题。
|
||||||
|
|
||||||
### 理解
|
### 理解
|
||||||
|
|
||||||
- 看一下 `logic.py`,你可能还记得讲义的内容。无需了解此文件中的所有内容,但请注意,此文件为不同类型的逻辑连接词定义了多个类。这些类可以相互组合,所以表达式 `And(Not(A), Or(B, C))` 代表逻辑语句:命题 A 是不正确的,同时,命题 B 或者命题 C 是正确的。(这里的“或”是同或,不是异或)
|
看一下 `logic.py`,你可能还记得讲义的内容。无需了解此文件中的所有内容,但请注意,此文件为不同类型的逻辑连接词定义了多个类。这些类可以相互组合,所以表达式 `And(Not(A), Or(B, C))` 代表逻辑语句:命题 A 是不正确的,同时,命题 B 或者命题 C 是正确的。(这里的“或”是同或,不是异或)
|
||||||
- 回想一下 `logic.py`,它还包含一个 函数 `model_check` 。`model_check` 输入知识库和查询结论。知识库是一个逻辑命题:如果知道多个逻辑语句,则可以将它们连接在一个表达式中。递归考虑所有可能的模型,如果知识库推理蕴含查询结论,则返回 `True`,否则返回 `False`。
|
|
||||||
- 现在,看看 `puzzle.py`,在顶部,我们定义了六个命题符号。例如,`AKnight` 表示“A 是骑士”的命题,`AKnave` 而表示“A 是流氓”的句子。我们也为字符 B 和 C 定义了类似的命题符号。
|
回想一下 `logic.py`,它还包含一个 函数 `model_check` 。`model_check` 输入知识库和查询结论。知识库是一个逻辑命题:如果知道多个逻辑语句,则可以将它们连接在一个表达式中。递归考虑所有可能的模型,如果知识库推理蕴含查询结论,则返回 `True`,否则返回 `False`。
|
||||||
- 接下来是四个不同的知识库 `knowledge0`, `knowledge1`, `knowledge2`, and `knowledge3`,它们将分别包含推断即将到来的谜题 0、1、2 和 3 的解决方案所需的知识。请注意,目前,这些知识库中的每一个都是空的。这就是你进来的地方!
|
|
||||||
- 这个 `puzzle.py` 的 `main` 函数在所有谜题上循环,并使用模型检查来计算,给定谜题的知识,无论每个角色是骑士还是无赖,打印出模型检查算法能够得出的任何结论。
|
现在,看看 `puzzle.py`,在顶部,我们定义了六个命题符号。例如,`AKnight` 表示“A 是骑士”的命题,`AKnave` 而表示“A 是流氓”的句子。我们也为字符 B 和 C 定义了类似的命题符号。
|
||||||
|
|
||||||
|
接下来是四个不同的知识库 `knowledge0`, `knowledge1`, `knowledge2`, and `knowledge3`,它们将分别包含推断即将到来的谜题 0、1、2 和 3 的解决方案所需的知识。请注意,目前,这些知识库中的每一个都是空的。这就是你进来的地方!
|
||||||
|
|
||||||
|
这个 `puzzle.py` 的 `main` 函数在所有谜题上循环,并使用模型检查来计算,给定谜题的知识,无论每个角色是骑士还是无赖,打印出模型检查算法能够得出的任何结论。
|
||||||
|
|
||||||
### 明确
|
### 明确
|
||||||
|
|
||||||
- 将知识添加到知识库 `knowledge0`, `knowledge1`, `knowledge2`, 和 `knowledge3` 中,以解决以下难题。
|
将知识添加到知识库 `knowledge0`, `knowledge1`, `knowledge2`, 和 `knowledge3` 中,以解决以下难题。
|
||||||
|
|
||||||
- 谜题 0 是背景中的谜题。它只包含一个简单的角色 A
|
- 谜题 0 是背景中的谜题。它只包含一个简单的角色 A
|
||||||
|
|
||||||
A 说:“我既是骑士又是流氓。”
|
A 说:“我既是骑士又是流氓。”
|
||||||
|
|
||||||
- 谜题 1 有两个角色:A 和 B
|
- 谜题 1 有两个角色:A 和 B
|
||||||
|
|
||||||
A 说:“我们都是流氓。”
|
A 说:“我们都是流氓。”
|
||||||
|
|
||||||
B 什么都没说。
|
B 什么都没说。
|
||||||
|
|
||||||
- 谜题 2 有两个角色:A 和 B
|
- 谜题 2 有两个角色:A 和 B
|
||||||
|
|
||||||
A 说:“我们是同一种身份。”
|
A 说:“我们是同一种身份。”
|
||||||
|
|
||||||
B 说:“我们不是同一种身份。”
|
B 说:“我们不是同一种身份。”
|
||||||
|
|
||||||
- 谜题 3 有三个角色:A,B 和 C
|
- 谜题 3 有三个角色:A,B 和 C
|
||||||
|
|
||||||
A 说:“我是骑士”或者 A 说:“我是流氓”(这里“或”是异或,不是同或),但你不知道 A 说的是哪句话。
|
A 说:“我是骑士”或者 A 说:“我是流氓”(这里“或”是异或,不是同或),但你不知道 A 说的是哪句话。
|
||||||
|
|
||||||
B 说:“A 说过‘我是流氓’。”
|
B 说:“A 说过‘我是流氓’。”
|
||||||
|
|
||||||
B 又说:“C 是流氓。”
|
B 又说:“C 是流氓。”
|
||||||
|
|
||||||
C 说:“A 是骑士。”
|
C 说:“A 是骑士。”
|
||||||
|
|
||||||
- 上述每个谜题中,每个角色要么是骑士,要么是流氓。骑士说的每一句话都是真的,流氓说的每一句话都是假的。
|
上述每个谜题中,每个角色要么是骑士,要么是流氓。骑士说的每一句话都是真的,流氓说的每一句话都是假的。
|
||||||
- 一旦你完成了一个问题的知识库,你应该能够运行 `python puzzle.py` 来查看谜题的解决方案。
|
|
||||||
|
一旦你完成了一个问题的知识库,你应该能够运行 `python puzzle.py` 来查看谜题的解决方案。
|
||||||
|
|
||||||
### 提示
|
### 提示
|
||||||
|
|
||||||
- 对于每个知识库,你可能想要编码两种不同类型的信息:(1)关于问题本身结构的信息(即骑士与流氓谜题定义中给出的信息),以及(2)关于角色实际说了什么的信息。
|
对于每个知识库,你可能想要编码两种不同类型的信息:(1)关于问题本身结构的信息(即骑士与流氓谜题定义中给出的信息),以及(2)关于角色实际说了什么的信息。
|
||||||
- 考虑一下,如果一个句子是由一个角色说出的,这意味着什么。在什么条件下这句话是真的?在什么条件下这个句子是假的?你如何将其表达为一个合乎逻辑的句子?
|
|
||||||
- 每个谜题都有多个可能的知识库,可以计算出正确的结果。你应该尝试选择一个能对谜题中的信息进行最直接的知识库,而不是自己进行逻辑推理。你还应该考虑谜题中信息最简洁的表达方式是什么。
|
|
||||||
|
|
||||||
- 例如,对于谜题 0,设置 `knowledge0=AKnave` 将产生正确的输出,因为通过我们自己的推理,我们知道 A 一定是一个无赖。但这样做违背了这个问题的精神:目标是让你的人工智能为你做推理。
|
考虑一下,如果一个句子是由一个角色说出的,这意味着什么。在什么条件下这句话是真的?在什么条件下这个句子是假的?你如何将其表达为一个合乎逻辑的句子?
|
||||||
- 您不需要(也不应该)修改 `logic.py` 来完成这个问题。
|
|
||||||
|
每个谜题都有多个可能的知识库,可以计算出正确的结果。你应该尝试选择一个能对谜题中的信息进行最直接的知识库,而不是自己进行逻辑推理。你还应该考虑谜题中信息最简洁的表达方式是什么。
|
||||||
|
|
||||||
|
例如,对于谜题 0,设置 `knowledge0=AKnave` 将产生正确的输出,因为通过我们自己的推理,我们知道 A 一定是一个无赖。但这样做违背了这个问题的精神:目标是让你的人工智能为你做推理。
|
||||||
|
|
||||||
|
您不需要(也不应该)修改 `logic.py` 来完成这个问题。
|
||||||
|
|
||||||
## 扫雷
|
## 扫雷
|
||||||
|
|
||||||
@@ -82,24 +95,28 @@ C 说:“A 是骑士。”
|
|||||||
|
|
||||||
#### 扫雷游戏
|
#### 扫雷游戏
|
||||||
|
|
||||||
- 扫雷器是一款益智游戏,由一个单元格网格组成,其中一些单元格包含隐藏的“地雷”。点击包含地雷的单元格会引爆地雷,导致用户输掉游戏。单击“安全”单元格(即不包含地雷的单元格)会显示一个数字,指示有多少相邻单元格包含地雷,其中相邻单元格是指从给定单元格向左、向右、向上、向下或对角线一个正方形的单元格。
|
扫雷器是一款益智游戏,由一个单元格网格组成,其中一些单元格包含隐藏的“地雷”。点击包含地雷的单元格会引爆地雷,导致用户输掉游戏。单击“安全”单元格(即不包含地雷的单元格)会显示一个数字,指示有多少相邻单元格包含地雷,其中相邻单元格是指从给定单元格向左、向右、向上、向下或对角线一个正方形的单元格。
|
||||||
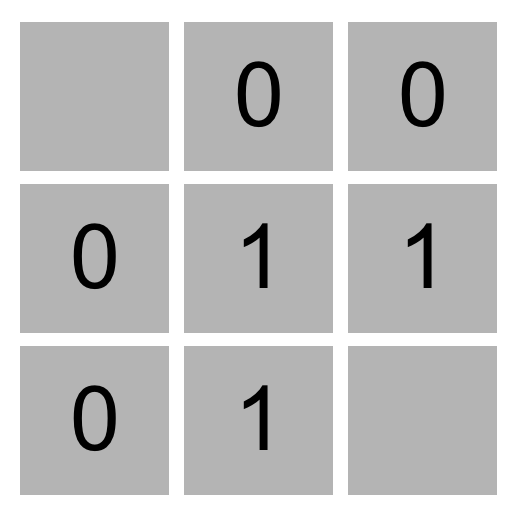
- 例如,在这个 3x3 扫雷游戏中,三个 1 值表示这些单元格中的每个单元格都有一个相邻的单元格,该单元格是地雷。四个 0 值表示这些单元中的每一个都没有相邻的地雷。
|
例如,在这个 3x3 扫雷游戏中,三个 1 值表示这些单元格中的每个单元格都有一个相邻的单元格,该单元格是地雷。四个 0 值表示这些单元中的每一个都没有相邻的地雷。
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
- 给定这些信息,玩家根据逻辑可以得出结论,右下角单元格中一定有地雷,左上角单元格中没有地雷,因为只有在这种情况下,其他单元格上的数字标签才会准确。
|
给定这些信息,玩家根据逻辑可以得出结论,右下角单元格中一定有地雷,左上角单元格中没有地雷,因为只有在这种情况下,其他单元格上的数字标签才会准确。
|
||||||
- 游戏的目标是标记(即识别)每个地雷。在游戏的许多实现中,包括本项目中的实现中,玩家可以通过右键单击单元格(或左键双击,具体取决于计算机)来标记地雷。
|
|
||||||
|
游戏的目标是标记(即识别)每个地雷。在游戏的许多实现中,包括本项目中的实现中,玩家可以通过右键单击单元格(或左键双击,具体取决于计算机)来标记地雷。
|
||||||
|
|
||||||
#### 命题逻辑
|
#### 命题逻辑
|
||||||
|
|
||||||
- 你在这个项目中的目标是建立一个可以玩扫雷游戏的人工智能。回想一下,基于知识的智能主体通过考虑他们的知识库来做出决策,并根据这些知识做出推断。
|
你在这个项目中的目标是建立一个可以玩扫雷游戏的人工智能。回想一下,基于知识的智能主体通过考虑他们的知识库来做出决策,并根据这些知识做出推断。
|
||||||
- 我们可以表示人工智能关于扫雷游戏的知识的一种方法是,使每个单元格成为命题变量,如果单元格包含地雷,则为真,否则为假。
|
|
||||||
|
我们可以表示人工智能关于扫雷游戏的知识的一种方法是,使每个单元格成为命题变量,如果单元格包含地雷,则为真,否则为假。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 我们现在掌握了什么信息?我们现在知道八个相邻的单元格中有一个是地雷。因此,我们可以写一个逻辑表达式,如下所示,表示其中一个相邻的单元格是地雷。
|
我们现在掌握了什么信息?我们现在知道八个相邻的单元格中有一个是地雷。因此,我们可以写一个逻辑表达式,如下所示,表示其中一个相邻的单元格是地雷。
|
||||||
|
|
||||||
- `Or(A,B,C,D,E,F,G,H)`
|
- `Or(A,B,C,D,E,F,G,H)`
|
||||||
- 但事实上,我们知道的比这个表达所说的要多。上面的逻辑命题表达了这样一种观点,即这八个变量中至少有一个是真的。但我们可以做一个更有力的陈述:我们知道八个变量中有一个是真的。这给了我们一个命题逻辑命题,如下所示。
|
|
||||||
|
但事实上,我们知道的比这个表达所说的要多。上面的逻辑命题表达了这样一种观点,即这八个变量中至少有一个是真的。但我们可以做一个更有力的陈述:我们知道八个变量中有一个是真的。这给了我们一个命题逻辑命题,如下所示。
|
||||||
|
|
||||||
```txt
|
```txt
|
||||||
Or(
|
Or(
|
||||||
@@ -114,82 +131,92 @@ Or(
|
|||||||
)
|
)
|
||||||
```
|
```
|
||||||
|
|
||||||
- 这是一个相当复杂的表达!这只是为了表达一个单元格中有 1 意味着什么。如果一个单元格有 2、3 或其他值,这个表达式可能会更长。
|
这是一个相当复杂的表达!这只是为了表达一个单元格中有 1 意味着什么。如果一个单元格有 2、3 或其他值,这个表达式可能会更长。
|
||||||
- 试图对这类问题进行模型检查也会很快变得棘手:在 8x8 网格(微软初级游戏模式使用的大小)上,我们有 64 个变量,因此需要检查
|
|
||||||
$$
|
|
||||||
2^64
|
|
||||||
$$
|
|
||||||
|
|
||||||
个可能的模型——太多了,计算机无法在任何合理的时间内计算。对于这个问题,我们需要更好地表达知识。
|
试图对这类问题进行模型检查也会很快变得棘手:在 8x8 网格(微软初级游戏模式使用的大小)上,我们有 64 个变量,因此需要检查$2^{64}$个可能的模型——太多了,计算机无法在任何合理的时间内计算。对于这个问题,我们需要更好地表达知识。
|
||||||
|
|
||||||
#### 知识表示
|
#### 知识表示
|
||||||
|
|
||||||
- 相反,我们将像下面这样表示人工智能知识的每一句话。
|
相反,我们将像下面这样表示人工智能知识的每一句话。
|
||||||
|
|
||||||
- `{A, B, C, D, E, F, G, H} = 1`
|
- `{A, B, C, D, E, F, G, H} = 1`
|
||||||
- 这种表示法中的每个逻辑命题都有两个部分:一个是网格中与提示数字有关的一组单元格 `cell`,另一个是数字计数 `count`,表示这些单元格中有多少是地雷。上面的逻辑命题说,在单元格 A、B、C、D、E、F、G 和 H 中,正好有 1 个是地雷。
|
|
||||||
- 为什么这是一个有用的表示?在某种程度上,它很适合某些类型的推理。考虑下面的游戏。
|
这种表示法中的每个逻辑命题都有两个部分:一个是网格中与提示数字有关的一组单元格 `cell`,另一个是数字计数 `count`,表示这些单元格中有多少是地雷。上面的逻辑命题说,在单元格 A、B、C、D、E、F、G 和 H 中,正好有 1 个是地雷。
|
||||||
|
|
||||||
|
为什么这是一个有用的表示?在某种程度上,它很适合某些类型的推理。考虑下面的游戏。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 利用左下数的知识,我们可以构造命题 `{D,E,G}=0`,意思是在 D、E 和 G 单元中,正好有 0 个是地雷。凭直觉,我们可以从这句话中推断出所有的单元格都必须是安全的。通过推理,每当我们有一个 `count` 为 0 的命题时,我们就知道该命题的所有 `cell` 都必须是安全的。
|
利用左下数的知识,我们可以构造命题 `{D,E,G}=0`,意思是在 D、E 和 G 单元中,正好有 0 个是地雷。凭直觉,我们可以从这句话中推断出所有的单元格都必须是安全的。通过推理,每当我们有一个 `count` 为 0 的命题时,我们就知道该命题的所有 `cell` 都必须是安全的。
|
||||||
- 同样,考虑下面的游戏。
|
|
||||||
|
同样,考虑下面的游戏。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 我们的人工智能会构建命题 `{E,F,H}=3`。凭直觉,我们可以推断出所有的 E、F 和 H 都是地雷。更一般地说,任何时候 `cell` 的数量等于 `count`,我们都知道这个命题的所有单元格都必须是地雷。
|
我们的人工智能会构建命题 `{E,F,H}=3`。凭直觉,我们可以推断出所有的 E、F 和 H 都是地雷。更一般地说,任何时候 `cell` 的数量等于 `count`,我们都知道这个命题的所有单元格都必须是地雷。
|
||||||
- 一般来说,我们只希望我们的命题是关于那些还不知道是安全的还是地雷的 `cell`。这意味着,一旦我们知道一个单元格是否是地雷,我们就可以更新我们的知识库来简化它们,并可能得出新的结论。
|
|
||||||
- 例如,如果我们的人工智能知道命题 `{A,B,C}=2`,那么我们还没有足够的信息来得出任何结论。但如果我们被告知 C 是安全的,我们可以将 C 从命题中完全删除,留下命题 `{A,B}=2`(顺便说一句,这确实让我们得出了一些新的结论)
|
一般来说,我们只希望我们的命题是关于那些还不知道是安全的还是地雷的 `cell`。这意味着,一旦我们知道一个单元格是否是地雷,我们就可以更新我们的知识库来简化它们,并可能得出新的结论。
|
||||||
- 同样,如果我们的人工智能知道命题 `{A,B,C}=2`,并且我们被告知 C 是一颗地雷,我们可以从命题中删除 C,并减少计数的值(因为 C 是导致该计数的地雷),从而得到命题 `{A、B}=1`。这是合乎逻辑的:如果 A、B 和 C 中有两个是地雷,并且我们知道 C 是地雷,那么 A 和 B 中一定有一个是地雷。
|
|
||||||
- 如果我们更聪明,我们可以做最后一种推理。
|
例如,如果我们的人工智能知道命题 `{A,B,C}=2`,那么我们还没有足够的信息来得出任何结论。但如果我们被告知 C 是安全的,我们可以将 C 从命题中完全删除,留下命题 `{A,B}=2`(顺便说一句,这确实让我们得出了一些新的结论)
|
||||||
|
|
||||||
|
同样,如果我们的人工智能知道命题 `{A,B,C}=2`,并且我们被告知 C 是一颗地雷,我们可以从命题中删除 C,并减少计数的值(因为 C 是导致该计数的地雷),从而得到命题 `{A、B}=1`。这是合乎逻辑的:如果 A、B 和 C 中有两个是地雷,并且我们知道 C 是地雷,那么 A 和 B 中一定有一个是地雷。
|
||||||
|
|
||||||
|
如果我们更聪明,我们可以做最后一种推理。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 考虑一下我们的人工智能根据中间顶部单元格和中间底部单元格会知道的两个命题。从中上角的单元格中,我们得到 `{A,B,C}=1`。从底部中间单元格中,我们得到 `{A,B,C,D,E}=2`。从逻辑上讲,我们可以推断出一个新的知识,即 `{D,E}=1`。毕竟,如果 A、B、C、D 和 E 中有两个是地雷,而 A、B 和 C 中只有一个是地雷的话,那么 D 和 E 必须是另一个地雷。
|
考虑一下我们的人工智能根据中间顶部单元格和中间底部单元格会知道的两个命题。从中上角的单元格中,我们得到 `{A,B,C}=1`。从底部中间单元格中,我们得到 `{A,B,C,D,E}=2`。从逻辑上讲,我们可以推断出一个新的知识,即 `{D,E}=1`。毕竟,如果 A、B、C、D 和 E 中有两个是地雷,而 A、B 和 C 中只有一个是地雷的话,那么 D 和 E 必须是另一个地雷。
|
||||||
- 更一般地说,任何时候我们有两个命题满足 `set1=count1` 和 `set2=count2`,其中 `set1` 是 `set2` 的子集,那么我们可以构造新的命题 `set2-set1=count2-count1`。考虑上面的例子,以确保你理解为什么这是真的。
|
|
||||||
- 因此,使用这种表示知识的方法,我们可以编写一个人工智能智能主体,它可以收集有关扫雷的知识,并希望选择它知道安全的单元格!
|
更一般地说,任何时候我们有两个命题满足 `set1=count1` 和 `set2=count2`,其中 `set1` 是 `set2` 的子集,那么我们可以构造新的命题 `set2-set1=count2-count1`。考虑上面的例子,以确保你理解为什么这是真的。
|
||||||
|
|
||||||
|
因此,使用这种表示知识的方法,我们可以编写一个人工智能智能主体,它可以收集有关扫雷的知识,并希望选择它知道安全的单元格!
|
||||||
|
|
||||||
### 理解
|
### 理解
|
||||||
|
|
||||||
- 这个项目有两个主要文件:`runner.py` 和 `minesweeper.py`。`minesweeper.py` 包含游戏本身和 AI 玩游戏的所有逻辑。`runner.py` 已经为你实现,它包含了运行游戏图形界面的所有代码。一旦你完成了 `minesweeper.py` 中所有必需的功能,你就可以运行 `python runner.py` 来玩扫雷了(或者让你的 AI 为你玩)!
|
这个项目有两个主要文件:`runner.py` 和 `minesweeper.py`。`minesweeper.py` 包含游戏本身和 AI 玩游戏的所有逻辑。`runner.py` 已经为你实现,它包含了运行游戏图形界面的所有代码。一旦你完成了 `minesweeper.py` 中所有必需的功能,你就可以运行 `python runner.py` 来玩扫雷了(或者让你的 AI 为你玩)!
|
||||||
- 让我们打开 `minesweeper.py` 来了解提供了什么。这个文件中定义了三个类,`Minesweeper`,负责处理游戏;`Sentence`,表示一个既包含一组 `cell` 又包含一个 `count` 的逻辑命题;以及 `MinesweeperAI`,它处理根据知识做出的推断。
|
|
||||||
- `Minesweeper` 类已经完全实现了。请注意,每个单元格都是一对 `(i,j)`,其中 `i` 是行号 (范围从 `0` 到 `height-1`),`j` 是列号 (范围从 `0` 到 `width-1`)。
|
让我们打开 `minesweeper.py` 来了解提供了什么。这个文件中定义了三个类,`Minesweeper`,负责处理游戏;`Sentence`,表示一个既包含一组 `cell` 又包含一个 `count` 的逻辑命题;以及 `MinesweeperAI`,它处理根据知识做出的推断。
|
||||||
- `Sentence` 类将用于表示背景中描述的形式的逻辑命题。每个命题中都有一组 `cell`,以及 `count` 表示其中有多少单元格是地雷。该类还包含函数 `known_mines` 和 `known_safes`,用于确定命题中的任何单元格是已知的地雷还是已知的安全单元格。它还包含函数 `mark_mine` 和 `mark_safe`,用于响应有关单元格的新信息来更新命题。
|
|
||||||
- 最后,`MinesweeperAI` 类将实现一个可以玩扫雷的 AI。AI 类跟踪许多值。`self.moves_made` 包含一组已经点击过的所有单元格,因此人工智能知道不要再选择这些单元格。`self.mines` 包含一组已知为地雷的所有单元格。`self.safes` 包含一组已知安全的所有单元格。而 `self.knowledge` 包含了人工智能知道是真的所有命题的列表。
|
`Minesweeper` 类已经完全实现了。请注意,每个单元格都是一对 `(i,j)`,其中 `i` 是行号 (范围从 `0` 到 `height-1`),`j` 是列号 (范围从 `0` 到 `width-1`)。
|
||||||
- `mark_mine` 函数为 `self.mines` 添加了一个单元格,因此 AI 知道这是一个地雷。它还循环遍历人工智能知识中的所有命题,并通知每个命题该单元格是地雷,这样,如果命题包含有关地雷的信息,它就可以相应地更新自己。`mark_safe` 函数也做同样的事情,只是针对安全单元格。
|
|
||||||
- 剩下的函数 `add_knowledge`、`make_safe_move` 和 `make_random_move` 由你完成!
|
`Sentence` 类将用于表示背景中描述的形式的逻辑命题。每个命题中都有一组 `cell`,以及 `count` 表示其中有多少单元格是地雷。该类还包含函数 `known_mines` 和 `known_safes`,用于确定命题中的任何单元格是已知的地雷还是已知的安全单元格。它还包含函数 `mark_mine` 和 `mark_safe`,用于响应有关单元格的新信息来更新命题。
|
||||||
|
|
||||||
|
最后,`MinesweeperAI` 类将实现一个可以玩扫雷的 AI。AI 类跟踪许多值。`self.moves_made` 包含一组已经点击过的所有单元格,因此人工智能知道不要再选择这些单元格。`self.mines` 包含一组已知为地雷的所有单元格。`self.safes` 包含一组已知安全的所有单元格。而 `self.knowledge` 包含了人工智能知道是真的所有命题的列表。
|
||||||
|
|
||||||
|
`mark_mine` 函数为 `self.mines` 添加了一个单元格,因此 AI 知道这是一个地雷。它还循环遍历人工智能知识中的所有命题,并通知每个命题该单元格是地雷,这样,如果命题包含有关地雷的信息,它就可以相应地更新自己。`mark_safe` 函数也做同样的事情,只是针对安全单元格。
|
||||||
|
|
||||||
|
剩下的函数 `add_knowledge`、`make_safe_move` 和 `make_random_move` 由你完成!
|
||||||
|
|
||||||
### 明确
|
### 明确
|
||||||
|
|
||||||
- 完成 `minesweeper.py` 中的 `Sentence` 类和 `MinesweeperAI` 类的实现。
|
完成 `minesweeper.py` 中的 `Sentence` 类和 `MinesweeperAI` 类的实现。
|
||||||
- 在 `Sentence` 类中,完成 `known_mines`、`known_safes`、`mark_mine` 和 `mark_safe` 的实现。
|
在 `Sentence` 类中,完成 `known_mines`、`known_safes`、`mark_mine` 和 `mark_safe` 的实现。
|
||||||
|
|
||||||
- `known_mines` 函数应该返回 `self.cells` 中已知为地雷的所有单元格的集合。
|
- `known_mines` 函数应该返回 `self.cells` 中已知为地雷的所有单元格的集合。
|
||||||
- `known_safes` 函数应该返回 `self.cells` 中已知安全的所有单元格的集合。
|
- `known_safes` 函数应该返回 `self.cells` 中已知安全的所有单元格的集合。
|
||||||
- `mark_mine` 函数应该首先检查单元格是否是命题中包含的单元格之一。
|
- `mark_mine` 函数应该首先检查单元格是否是命题中包含的单元格之一。
|
||||||
|
- 如果 `cell` 在命题中,函数应该更新命题,使单元格不再在命题中但仍然表示一个逻辑正确的命题,因为该 `cell` 已知是地雷。
|
||||||
|
- 如果命题中没有 `cell`,则不需要采取任何行动。
|
||||||
|
- `mark_safe` 函数应该首先检查单元格是否是命题中包含的单元格之一。
|
||||||
|
- 如果 `cell` 在命题中,则函数应更新命题,使单元格不再在命题中但仍然表示一个逻辑正确的命题,因为该 `cell` 已知是安全的。
|
||||||
|
- 如果命题中没有 `cell`,则不需要采取任何行动。
|
||||||
|
|
||||||
- 如果 `cell` 在命题中,函数应该更新命题,使单元格不再在命题中但仍然表示一个逻辑正确的命题,因为该 `cell` 已知是地雷。
|
在 `MinesweeperAI` 类中,完成 `add_knowledge`、`make_safe_move` 和 `make_random_move` 的实现。
|
||||||
- 如果命题中没有 `cell`,则不需要采取任何行动。
|
|
||||||
- `mark_safe` 函数应该首先检查单元格是否是命题中包含的单元格之一。
|
|
||||||
|
|
||||||
- 如果 `cell` 在命题中,则函数应更新命题,使单元格不再在命题中但仍然表示一个逻辑正确的命题,因为该 `cell` 已知是安全的。
|
- `add_knowledge` 应该接受一个单元格(表示为元组 `(i,j)`)及其相应的 `count`,并使用 AI 可以推断的任何新信息更新 `self.mines`、`self.safes`、`self.moves_made` 和 `self.knowledge`,因为该单元格是已知的安全单元格,其附近有计数地雷。
|
||||||
- 如果命题中没有 `cell`,则不需要采取任何行动。
|
- 该函数应将该 `cell` 标记为游戏中的一个动作。
|
||||||
- 在 `MinesweeperAI` 类中,完成 `add_knowledge`、`make_safe_move` 和 `make_random_move` 的实现。
|
- 函数应该将 `cell` 标记为安全单元格,同时更新包含该单元格的任何命题。
|
||||||
|
- 该函数应该根据 `cell` 和 `count` 的值,在人工智能的知识库中添加一个新命题,以表明 `cell` 的邻居有 `count` 是地雷。请确保在命题中只包含状态尚未确定的单元格。
|
||||||
|
- 如果根据 `self.knowledge` 中的任何一个命题,新的单元格可以被标记为安全的或地雷,那么函数应该这样做。
|
||||||
|
- 如果根据 `self.knowledge` 中的任何一个命题,可以推断出新的命题(使用背景技术中描述的子集方法),那么这些命题也应该添加到知识库中。
|
||||||
|
- 请注意,每当你对人工智能的知识做出任何改变时,都有可能得出以前不可能的新推论。如果可能的话,请确保将这些新的推断添加到知识库中。
|
||||||
|
|
||||||
- `add_knowledge` 应该接受一个单元格(表示为元组 `(i,j)`)及其相应的 `count`,并使用 AI 可以推断的任何新信息更新 `self.mines`、`self.safes`、`self.moves_made` 和 `self.knowledge`,因为该单元格是已知的安全单元格,其附近有计数地雷。
|
|
||||||
|
|
||||||
- 该函数应将该 `cell` 标记为游戏中的一个动作。
|
|
||||||
- 函数应该将 `cell` 标记为安全单元格,同时更新包含该单元格的任何命题。
|
|
||||||
- 该函数应该根据 `cell` 和 `count` 的值,在人工智能的知识库中添加一个新命题,以表明 `cell` 的邻居有 `count` 是地雷。请确保在命题中只包含状态尚未确定的单元格。
|
|
||||||
- 如果根据 `self.knowledge` 中的任何一个命题,新的单元格可以被标记为安全的或地雷,那么函数应该这样做。
|
|
||||||
- 如果根据 `self.knowledge` 中的任何一个命题,可以推断出新的命题(使用背景技术中描述的子集方法),那么这些命题也应该添加到知识库中。
|
|
||||||
- 请注意,每当你对人工智能的知识做出任何改变时,都有可能得出以前不可能的新推论。如果可能的话,请确保将这些新的推断添加到知识库中。
|
|
||||||
- `make_safe_move` 应该返回一个已知安全的选择 `(i,j)`。
|
- `make_safe_move` 应该返回一个已知安全的选择 `(i,j)`。
|
||||||
|
|
||||||
- 必须知道返回的动作是安全的,而不是已经做出的动作。
|
- 必须知道返回的动作是安全的,而不是已经做出的动作。
|
||||||
- 如果无法保证安全移动,则函数应返回 `None`。
|
- 如果无法保证安全移动,则函数应返回 `None`。
|
||||||
- 该函数不应修改 `self.moves_made`、`self.mines`、`self.safes` 或 `self.knowledge`。
|
- 该函数不应修改 `self.moves_made`、`self.mines`、`self.safes` 或 `self.knowledge`。
|
||||||
- `make_random_move` 应该返回一个随机选择 `(i,j)`。
|
|
||||||
|
|
||||||
|
- `make_random_move` 应该返回一个随机选择 `(i,j)`。
|
||||||
- 如果无法安全移动,将调用此功能:如果人工智能不知道移动到哪里,它将选择随机移动。
|
- 如果无法安全移动,将调用此功能:如果人工智能不知道移动到哪里,它将选择随机移动。
|
||||||
- 此举不得是已经采取的行动。
|
- 此举不得是已经采取的行动。
|
||||||
- 此举决不能是已知的地雷行动。
|
- 此举决不能是已知的地雷行动。
|
||||||
|
|||||||
@@ -23,27 +23,37 @@
|
|||||||
|
|
||||||
## 基础知识
|
## 基础知识
|
||||||
|
|
||||||
- 基于知识的智能主体 (Knowledge-Based Agents)
|
### 基于知识的智能主体 (Knowledge-Based Agents)
|
||||||
- 智能主体通过对内部的知识表征进行操作来推理得出结论。
|
|
||||||
- “根据知识推理得出结论”是什么意思?
|
智能主体通过对内部的知识表征进行操作来推理得出结论。
|
||||||
- 让我们开始用哈利波特的例子来回答这个问题。考虑以下句子:
|
|
||||||
1. 如果没有下雨,哈利今天会去拜访海格。
|
“根据知识推理得出结论”是什么意思?
|
||||||
2. 哈利今天拜访了海格或邓布利多,但没有同时拜访他们。
|
|
||||||
3. 哈利今天拜访了邓布利多。
|
让我们开始用哈利波特的例子来回答这个问题。考虑以下句子:
|
||||||
- 基于这三个句子,我们可以回答“今天下雨了吗?”这个问题,尽管没有一个单独的句子告诉我们今天是否下雨,根据推理我们可以得出结论“今天下雨了”。
|
|
||||||
- 陈述句 (Sentence)
|
1. 如果没有下雨,哈利今天会去拜访海格。
|
||||||
- 陈述句是知识表示语言中关于世界的断言。陈述句是人工智能存储知识并使用它来推断新信息的方式。
|
2. 哈利今天拜访了海格或邓布利多,但没有同时拜访他们。
|
||||||
|
3. 哈利今天拜访了邓布利多。
|
||||||
|
基于这三个句子,我们可以回答“今天下雨了吗?”这个问题,尽管没有一个单独的句子告诉我们今天是否下雨,根据推理我们可以得出结论“今天下雨了”。
|
||||||
|
|
||||||
|
### 陈述句 (Sentence)
|
||||||
|
|
||||||
|
陈述句是知识表示语言中关于世界的断言。陈述句是人工智能存储知识并使用它来推断新信息的方式。
|
||||||
|
|
||||||
## 命题逻辑 (Propositional Logic)
|
## 命题逻辑 (Propositional Logic)
|
||||||
|
|
||||||
命题逻辑基于命题。命题是关于世界的陈述,可以是真也可以是假,正如上面例子中的句子。
|
命题逻辑基于命题。命题是关于世界的陈述,可以是真也可以是假,正如上面例子中的句子。
|
||||||
|
|
||||||
- 命题符号 (Propositional Symbols)
|
### 命题符号 (Propositional Symbols)
|
||||||
- 命题符号通常是用于表示命题的字母$P、Q、R$
|
|
||||||
- 逻辑连接词 (Logical Connectives)
|
命题符号通常是用于表示命题的字母$P、Q、R$
|
||||||
- 逻辑连接词是连接命题符号的逻辑符号,以便以更复杂的方式对世界进行推理。
|
|
||||||
- **Not**** ****(**$\lnot$**)** 逻辑非:命题真值的反转。例如,如果 $P$:“正在下雨”,那么 $¬P$:“没有下雨”。
|
### 逻辑连接词 (Logical Connectives)
|
||||||
- 真值表用于将所有可能的真值赋值与命题进行比较。该工具将帮助我们更好地理解与不同逻辑连接词相关联的命题的真值。例如,下面是我们的第一个真值表:
|
|
||||||
|
逻辑连接词是连接命题符号的逻辑符号,以便以更复杂的方式对世界进行推理。
|
||||||
|
|
||||||
|
- <strong>Not</strong><strong> </strong><strong>(</strong>$\lnot$<strong>)</strong> 逻辑非:命题真值的反转。例如,如果 $P$:“正在下雨”,那么 $¬P$:“没有下雨”。
|
||||||
|
真值表用于将所有可能的真值赋值与命题进行比较。该工具将帮助我们更好地理解与不同逻辑连接词相关联的命题的真值。例如,下面是我们的第一个真值表:
|
||||||
|
|
||||||
| $P$ | $\lnot P$ |
|
| $P$ | $\lnot P$ |
|
||||||
| -------- | --------- |
|
| -------- | --------- |
|
||||||
@@ -68,11 +78,11 @@
|
|||||||
| 1 | 0 | 1 |
|
| 1 | 0 | 1 |
|
||||||
| 1 | 1 | 1 |
|
| 1 | 1 | 1 |
|
||||||
|
|
||||||
- 值得一提的是,Or 有两种类型:同或 Or 和异或 Or。在异或中,如果$P\lor Q$为真,则$P∧Q$为假。也就是说,一个异或要求它只有一个论点为真,而不要求两者都为真。如果$P、Q$或$P∧Q$中的任何一个为真,则包含或为真。在 Or($\lor$) 的情况下,意图是一个包含的 Or。
|
值得一提的是,Or 有两种类型:同或 Or 和异或 Or。在异或中,如果$P\lor Q$为真,则$P∧Q$为假。也就是说,一个异或要求它只有一个论点为真,而不要求两者都为真。如果$P、Q$或$P∧Q$中的任何一个为真,则包含或为真。在 Or($\lor$) 的情况下,意图是一个包含的 Or。
|
||||||
|
|
||||||
- **Implication (→)** 逻辑蕴含:表示“如果$P$,则$Q$的结构。例如,如果$P$:“正在下雨”,$Q$:“我在室内”,则$P→ Q$的意思是“如果下雨,那么我在室内。”在$P$的情况下,意味着$Q$,$P$被称为前件,$Q$ 被称为后件。
|
- **Implication (→)** 逻辑蕴含:表示“如果$P$,则$Q$的结构。例如,如果$P$:“正在下雨”,$Q$:“我在室内”,则$P→ Q$的意思是“如果下雨,那么我在室内。”在$P$的情况下,意味着$Q$,$P$被称为前件,$Q$ 被称为后件。
|
||||||
|
|
||||||
- 当前件为真时,在后件为真的情况下,整个蕴含逻辑为真(这是有道理的:如果下雨,我在室内,那么“如果下雨,那么我在室内”这句话是真的)。当前件为真时,如果后件为假,则蕴含逻辑为假(如果下雨时我在外面,那么“如果下雨,那么我在室内”这句话是假的)。然而,当前件为假时,无论后件如何,蕴含逻辑总是真的。这有时可能是一个令人困惑的概念。从逻辑上讲,我们不能从蕴含中学到任何东西$(P→ Q)$如果前件 ($P$) 为假。看一下我们的例子,如果没有下雨,这个蕴含逻辑并没有说我是否在室内的问题。我可能是一个室内型的人,即使不下雨也不在外面走,或者我可能是一个室外型的人,不下雨的时候一直在外面。当前件是假的,我们说蕴含逻辑是真的。
|
当前件为真时,在后件为真的情况下,整个蕴含逻辑为真(这是有道理的:如果下雨,我在室内,那么“如果下雨,那么我在室内”这句话是真的)。当前件为真时,如果后件为假,则蕴含逻辑为假(如果下雨时我在外面,那么“如果下雨,那么我在室内”这句话是假的)。然而,当前件为假时,无论后件如何,蕴含逻辑总是真的。这有时可能是一个令人困惑的概念。从逻辑上讲,我们不能从蕴含中学到任何东西$(P→ Q)$如果前件 ($P$) 为假。看一下我们的例子,如果没有下雨,这个蕴含逻辑并没有说我是否在室内的问题。我可能是一个室内型的人,即使不下雨也不在外面走,或者我可能是一个室外型的人,不下雨的时候一直在外面。当前件是假的,我们说蕴含逻辑是真的。
|
||||||
|
|
||||||
| $P$ | $Q$ | $P\to Q$ |
|
| $P$ | $Q$ | $P\to Q$ |
|
||||||
| --- | --- | -------- |
|
| --- | --- | -------- |
|
||||||
@@ -91,31 +101,44 @@
|
|||||||
| 1 | 0 | 0 |
|
| 1 | 0 | 0 |
|
||||||
| 1 | 1 | 1 |
|
| 1 | 1 | 1 |
|
||||||
|
|
||||||
- 模型 (Model)
|
### 模型 (Model)
|
||||||
- 模型是对每个命题的真值赋值。重申一下,命题是关于世界的陈述,可以是真也可以是假。然而,关于世界的知识体现在这些命题的真值中。模型是提供有关世界的信息的真值赋值。
|
|
||||||
- 例如,如果 $P$:“正在下雨。”和 $Q$:“今天是星期二。”,模型可以是以下真值赋值:$\set{P = True, Q = False}$。此模型表示正在下雨,但不是星期二。然而,在这种情况下有更多可能的模型(例如,$\set{P = True, Q = True}$,星期二并且下雨)。事实上,可能模型的数量是命题数量的 2 次方。在这种情况下,我们有 2 个命题,所以 $2^2=4$ 个可能的模型。
|
模型是对每个命题的真值赋值。重申一下,命题是关于世界的陈述,可以是真也可以是假。然而,关于世界的知识体现在这些命题的真值中。模型是提供有关世界的信息的真值赋值。
|
||||||
- 知识库 (Knowledge Base (KB))
|
|
||||||
- 知识库是基于知识的智能主题已知的一组陈述句。这是关于人工智能以命题逻辑语句的形式提供的关于世界的知识,可用于对世界进行额外的推理。
|
例如,如果 $P$:“正在下雨。”和 $Q$:“今天是星期二。”,模型可以是以下真值赋值:$\set{P = True, Q = False}$。此模型表示正在下雨,但不是星期二。然而,在这种情况下有更多可能的模型(例如,$\set{P = True, Q = True}$,星期二并且下雨)。事实上,可能模型的数量是命题数量的 2 次方。在这种情况下,我们有 2 个命题,所以 $2^2=4$ 个可能的模型。
|
||||||
- 蕴含推理 (Entailment ($\vDash$))
|
|
||||||
- 如果 $α ⊨ β$($α$蕴含推理出 $β$),那么在任何 $α$为真的世界中,$β$也为真。
|
### 知识库 (Knowledge Base (KB))
|
||||||
- 例如,如果 $α$:“今天是一月的星期二”和 $β$:“今天是星期二”,那么我们知道 $α ⊨ β$。如果确实是一月的星期二,我们也知道这是星期二。蕴含推理不同于逻辑蕴含。逻辑蕴涵是两个命题之间的逻辑连接。另一方面,推理蕴含关系是指如果 $α$中的所有信息都为真,则 $β$中的所有信息都为真。
|
|
||||||
|
知识库是基于知识的智能主题已知的一组陈述句。这是关于人工智能以命题逻辑语句的形式提供的关于世界的知识,可用于对世界进行额外的推理。
|
||||||
|
|
||||||
|
### 蕴含推理 (Entailment ($\vDash$))
|
||||||
|
|
||||||
|
如果 $α ⊨ β$($α$蕴含推理出 $β$),那么在任何 $α$为真的世界中,$β$也为真。
|
||||||
|
|
||||||
|
例如,如果 $α$:“今天是一月的星期二”和 $β$:“今天是星期二”,那么我们知道 $α ⊨ β$。如果确实是一月的星期二,我们也知道这是星期二。蕴含推理不同于逻辑蕴含。逻辑蕴涵是两个命题之间的逻辑连接。另一方面,推理蕴含关系是指如果 $α$中的所有信息都为真,则 $β$中的所有信息都为真。
|
||||||
|
|
||||||
## 推理 (Inference)
|
## 推理 (Inference)
|
||||||
|
|
||||||
推理是从原有命题推导出新命题的过程。
|
推理是从原有命题推导出新命题的过程。
|
||||||
|
|
||||||
- 模型检查算法 (Model Checking algorithm)
|
### 模型检查算法 (Model Checking algorithm)
|
||||||
- 确定是否$KB ⊨ α$(换句话说,回答问题:“我们能否根据我们的知识库得出结论 $α$为真?”)
|
|
||||||
- 枚举所有可能的模型。
|
|
||||||
- 如果在 $KB$为真的每个模型中,$α$也为真,则 $KB ⊨ α$。
|
|
||||||
- 一个例子
|
|
||||||
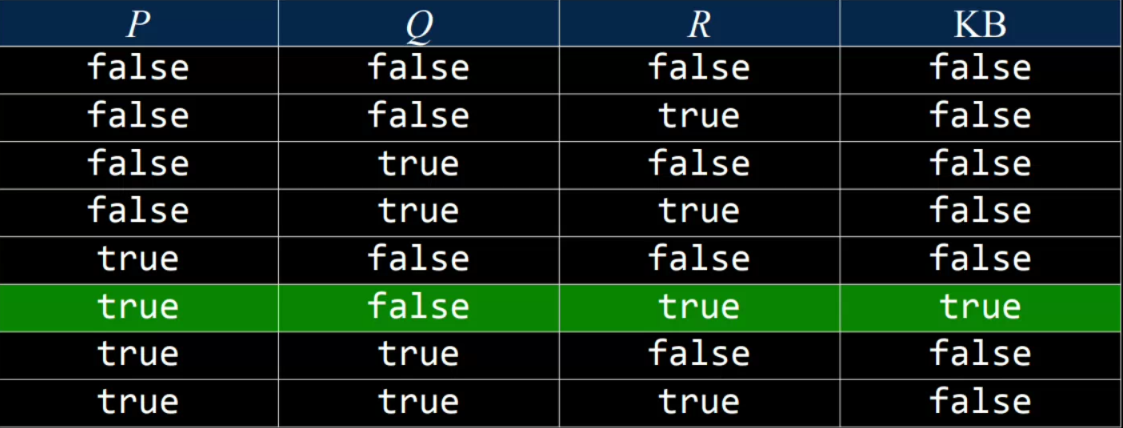
- $P$: 今天是星期四,$Q$: 今天下雨,$R$: 我将出门跑步$
|
|
||||||
- $KB$: 如果今天是星期四并且不下雨,那我将出门跑步;今天是星期四;今天不下雨。$(P\land\lnot Q)\to R,P,\lnot Q$
|
|
||||||
- 查询结论 (query): $R$
|
|
||||||
|
|
||||||
|
确定是否$KB ⊨ α$(换句话说,回答问题:“我们能否根据我们的知识库得出结论 $α$为真?”)
|
||||||
|
|
||||||
- 接下来,让我们看看如何将知识和逻辑表示为代码。
|
- 枚举所有可能的模型。
|
||||||
|
- 如果在 $KB$为真的每个模型中,$α$也为真,则 $KB ⊨ α$。
|
||||||
|
|
||||||
|
#### 一个例子
|
||||||
|
|
||||||
|
$P$: 今天是星期四,$Q$: 今天下雨,$R$: 我将出门跑步$
|
||||||
|
|
||||||
|
$KB$: 如果今天是星期四并且不下雨,那我将出门跑步;今天是星期四;今天不下雨。$(P\land\lnot Q)\to R,P,\lnot Q$
|
||||||
|
|
||||||
|
查询结论 (query): $R$
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
接下来,让我们看看如何将知识和逻辑表示为代码。
|
||||||
|
|
||||||
```python
|
```python
|
||||||
from logic import * # 创建新类,每个类都有一个名称或一个符号,代表每个命题。
|
from logic import * # 创建新类,每个类都有一个名称或一个符号,代表每个命题。
|
||||||
@@ -131,13 +154,14 @@ dumbledore # 哈利拜访了邓布利多。请注意,虽然之前的命题包
|
|||||||
)
|
)
|
||||||
```
|
```
|
||||||
|
|
||||||
- 要运行模型检查算法,需要以下信息:
|
要运行模型检查算法,需要以下信息:
|
||||||
|
|
||||||
- 知识库 (KB),将用于得出推论
|
- 知识库 (KB),将用于得出推论
|
||||||
- 一个查询结论 (query),或者我们感兴趣的命题是否被$KB$包含
|
- 一个查询结论 (query),或者我们感兴趣的命题是否被$KB$包含
|
||||||
- 命题符号,所有使用的符号(或原子命题)的列表(在我们的例子中,这些是 rain、hagrid 和 dumbledore)
|
- 命题符号,所有使用的符号(或原子命题)的列表(在我们的例子中,这些是 rain、hagrid 和 dumbledore)
|
||||||
- 模型,将真值和假值分配给命题
|
- 模型,将真值和假值分配给命题
|
||||||
- 模型检查算法如下所示:
|
|
||||||
|
模型检查算法如下所示:
|
||||||
|
|
||||||
```python
|
```python
|
||||||
def check_all(knowledge, query, symbols, model):# 如果模型对每个符号都有一个赋值
|
def check_all(knowledge, query, symbols, model):# 如果模型对每个符号都有一个赋值
|
||||||
@@ -161,11 +185,11 @@ def check_all(knowledge, query, symbols, model):# 如果模型对每个符号都
|
|||||||
return(check_all(knowledge, query, remaining, model_true) and check_all(knowledge, query, remaining, model_false))
|
return(check_all(knowledge, query, remaining, model_true) and check_all(knowledge, query, remaining, model_false))
|
||||||
```
|
```
|
||||||
|
|
||||||
- 请注意,我们只对$KB$为真的模型感兴趣。如果$KB$为假,那么我们知道真实的条件并没有出现在这些模型中,使它们与我们的案例无关。
|
请注意,我们只对$KB$为真的模型感兴趣。如果$KB$为假,那么我们知道真实的条件并没有出现在这些模型中,使它们与我们的案例无关。
|
||||||
|
|
||||||
> 另一个例子:假设 $P$:Harry 扮演找球手,$Q$:Oliver 扮演守门员,$R$:Gryffindor 获胜。我们的$KB$指定$P$, $Q$, $(P ∧ Q) \to R$。换句话说,我们知道$P$为真,即 Harry 扮演找球手,$Q$为真,即 Oliver 扮演守门员,并且如果$P$和$Q$都为真,那么$R$也为真,这意味着 Gryffindor 赢得了比赛。现在想象一个模型,其中 Harry 扮演击球手而不是找球手 (因此,Harry 没有扮演找球手,$¬P$)。嗯,在这种情况下,我们不关心 Gryffindor 是否赢了 (无论$R$是否为真),因为我们的$KB$中有信息表明 Harry 扮演的是找球手而不是击球手。我们只对$P$和$Q$ 为真的模型感兴趣。)
|
> 另一个例子:假设 $P$:Harry 扮演找球手,$Q$:Oliver 扮演守门员,$R$:Gryffindor 获胜。我们的$KB$指定$P$, $Q$, $(P ∧ Q) \to R$。换句话说,我们知道$P$为真,即 Harry 扮演找球手,$Q$为真,即 Oliver 扮演守门员,并且如果$P$和$Q$都为真,那么$R$也为真,这意味着 Gryffindor 赢得了比赛。现在想象一个模型,其中 Harry 扮演击球手而不是找球手 (因此,Harry 没有扮演找球手,$¬P$)。嗯,在这种情况下,我们不关心 Gryffindor 是否赢了 (无论$R$是否为真),因为我们的$KB$中有信息表明 Harry 扮演的是找球手而不是击球手。我们只对$P$和$Q$ 为真的模型感兴趣。)
|
||||||
|
|
||||||
- 此外,`check_all` 函数的工作方式是递归的。也就是说,它选择一个命题符号,创建两个模型,其中一个符号为真,另一个为假,然后再次调用自己,现在有两个模型因该命题符号的真值分配不同而不同。该函数将继续这样做,直到所有符号都已在模型中分配了真值,使 `symbol` 符号为空。一旦它为空(由 `if not symbols` 行标识),在函数的每个实例中(其中每个实例都包含不同的模型),函数检查$KB$是否为给定的有效模型。如果$KB$在此模型中为真,函数将检查查询结论是否为真,如前所述。
|
此外,`check_all` 函数的工作方式是递归的。也就是说,它选择一个命题符号,创建两个模型,其中一个符号为真,另一个为假,然后再次调用自己,现在有两个模型因该命题符号的真值分配不同而不同。该函数将继续这样做,直到所有符号都已在模型中分配了真值,使 `symbol` 符号为空。一旦它为空(由 `if not symbols` 行标识),在函数的每个实例中(其中每个实例都包含不同的模型),函数检查$KB$是否为给定的有效模型。如果$KB$在此模型中为真,函数将检查查询结论是否为真,如前所述。
|
||||||
|
|
||||||
## 知识工程 (Knowledge Engineering)
|
## 知识工程 (Knowledge Engineering)
|
||||||
|
|
||||||
@@ -173,144 +197,149 @@ def check_all(knowledge, query, symbols, model):# 如果模型对每个符号都
|
|||||||
|
|
||||||
### 推理规则 (Inference Rules)
|
### 推理规则 (Inference Rules)
|
||||||
|
|
||||||
- 模型检查不是一种有效的算法,因为它必须在给出答案之前考虑每个可能的模型(提醒:如果在$KB$为真的所有模型(真值分配)下,查询结论$R$为真,则$R$ 也为真)。推理规则允许我们根据现有知识生成新信息,而无需考虑所有可能的模型。
|
模型检查不是一种有效的算法,因为它必须在给出答案之前考虑每个可能的模型(提醒:如果在$KB$为真的所有模型(真值分配)下,查询结论$R$为真,则$R$ 也为真)。推理规则允许我们根据现有知识生成新信息,而无需考虑所有可能的模型。
|
||||||
- 推理规则通常使用将顶部部分(前提)与底部部分(结论)分开的水平条表示。前提是我们有什么知识,结论是根据这个前提可以产生什么知识。
|
|
||||||
|
|
||||||

|
推理规则通常使用将顶部部分(前提)与底部部分(结论)分开的水平条表示。前提是我们有什么知识,结论是根据这个前提可以产生什么知识。
|
||||||
|
|
||||||
- 肯定前件 (Modus Ponens)
|

|
||||||
|
|
||||||
- 如果我们知道一个蕴涵及其前件为真,那么后件也为真。
|
#### 肯定前件 (Modus Ponens)
|
||||||
|
|
||||||
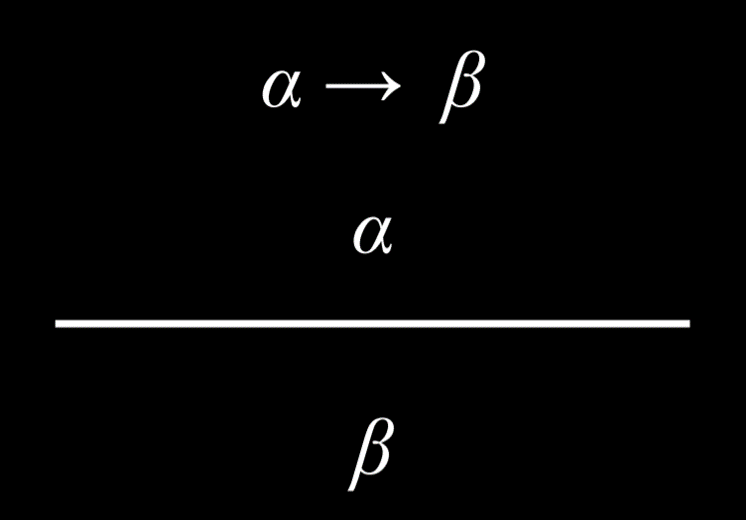
|
如果我们知道一个蕴涵及其前件为真,那么后件也为真。
|
||||||
|
|
||||||
- 合取消除 (And Elimination)
|
|
||||||
|
|
||||||
- 如果 And 命题为真,则其中的任何一个原子命题也为真。例如,如果我们知道哈利与罗恩和赫敏是朋友,我们就可以得出结论,哈利与赫敏是朋友。
|
#### 合取消除 (And Elimination)
|
||||||
|
|
||||||
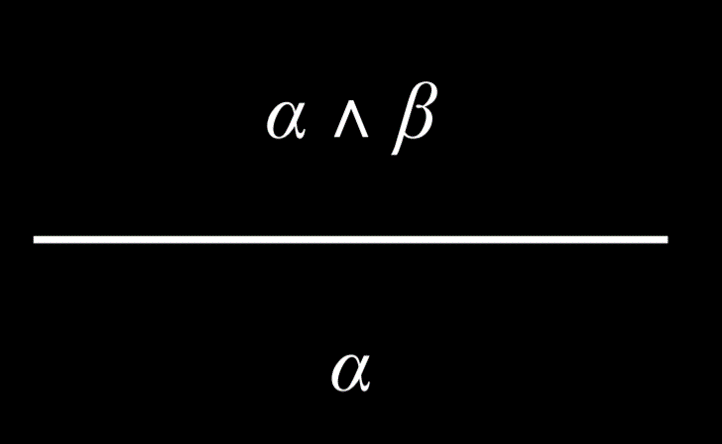
|
如果 And 命题为真,则其中的任何一个原子命题也为真。例如,如果我们知道哈利与罗恩和赫敏是朋友,我们就可以得出结论,哈利与赫敏是朋友。
|
||||||
|
|
||||||
- 双重否定消除 (Double Negation Elimination)
|
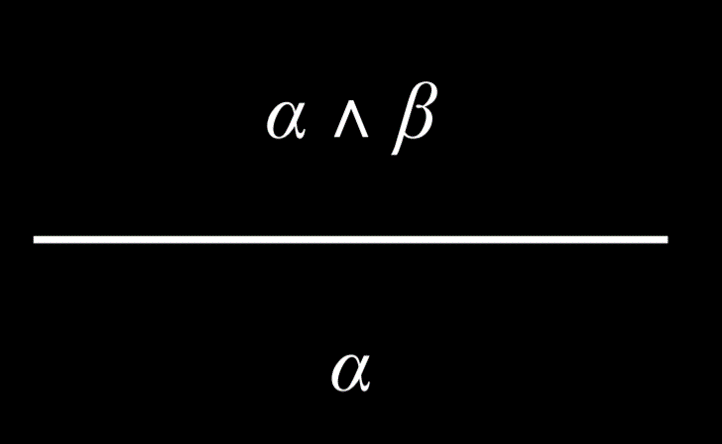
|
||||||
|
|
||||||
- 被两次否定的命题为真。例如,考虑命题“哈利没有通过考试是不正确的”。这两个否定相互抵消,将命题“哈利通过考试”标记为真。
|
#### 双重否定消除 (Double Negation Elimination)
|
||||||
|
|
||||||
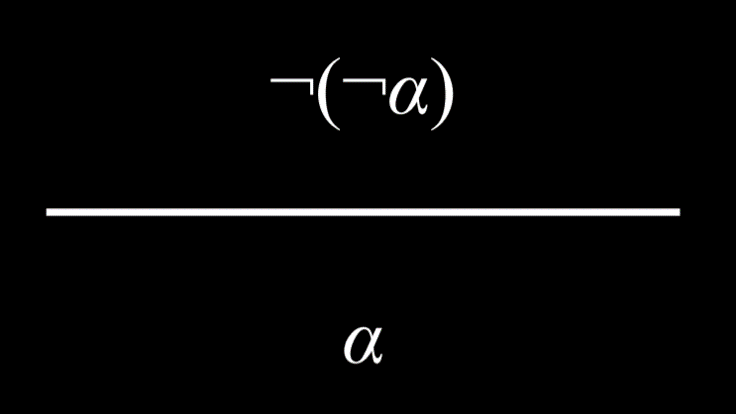
|
被两次否定的命题为真。例如,考虑命题“哈利没有通过考试是不正确的”。这两个否定相互抵消,将命题“哈利通过考试”标记为真。
|
||||||
|
|
||||||
- 蕴含消除 (Implication Elimination)
|
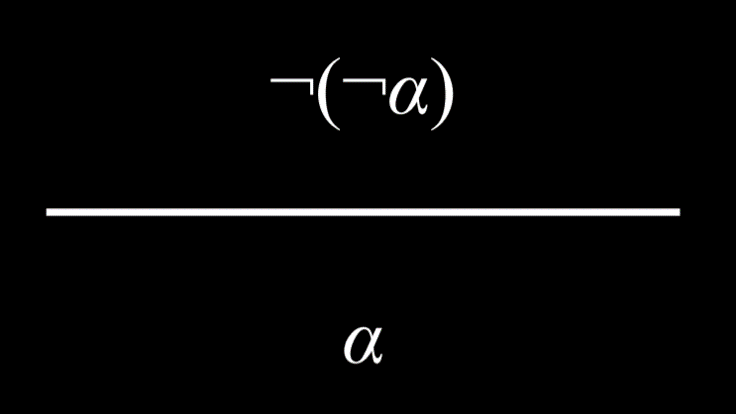
|
||||||
|
|
||||||
- 蕴涵等价于被否定的前件和后件之间的 Or 关系。例如,命题“如果正在下雨,哈利在室内”等同于命题“(没有下雨) 或 (哈利在室内)”。
|
#### 蕴含消除 (Implication Elimination)
|
||||||
|
|
||||||
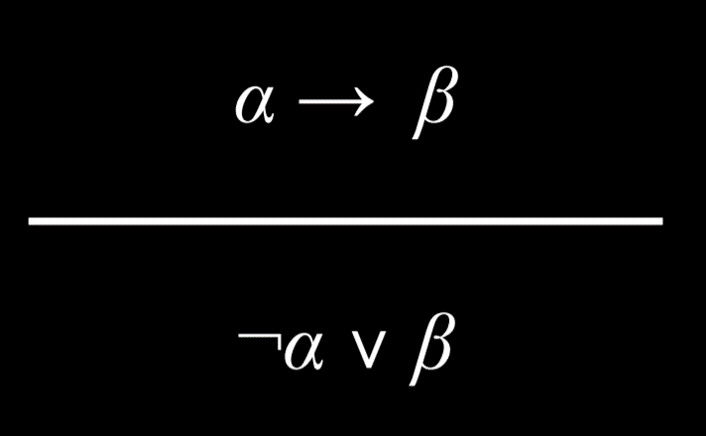
|
蕴涵等价于被否定的前件和后件之间的 Or 关系。例如,命题“如果正在下雨,哈利在室内”等同于命题“(没有下雨) 或 (哈利在室内)”。
|
||||||
|
|
||||||
| $P$ | $Q$ | $P\to Q$ | $\lnot P\lor Q$ |
|
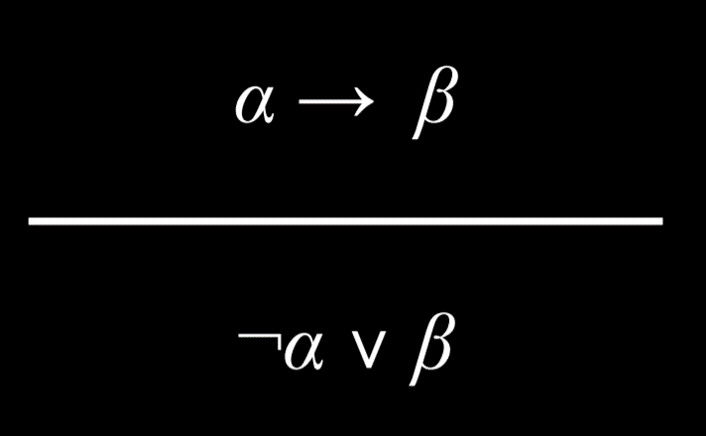
|
||||||
| --- | --- | -------- | --------------- |
|
|
||||||
| 0 | 0 | 1 | 1 |
|
|
||||||
| 0 | 1 | 1 | 1 |
|
|
||||||
| 1 | 0 | 0 | 0 |
|
|
||||||
| 1 | 1 | 1 | 1 |
|
|
||||||
|
|
||||||
- 等值消除 (Biconditional Elimination)
|
| $P$ | $Q$ | $P\to Q$ | $\lnot P\lor Q$ |
|
||||||
|
| --- | --- | -------- | --------------- |
|
||||||
|
| 0 | 0 | 1 | 1 |
|
||||||
|
| 0 | 1 | 1 | 1 |
|
||||||
|
| 1 | 0 | 0 | 0 |
|
||||||
|
| 1 | 1 | 1 | 1 |
|
||||||
|
|
||||||
- 等值命题等价于蕴涵及其逆命题的 And 关系。例如,“当且仅当 Harry 在室内时才下雨”等同于 (“如果正在下雨,Harry 在室内”和“如果 Harry 在室内,则正在下雨”)。
|
#### 等值消除 (Biconditional Elimination)
|
||||||
|
|
||||||
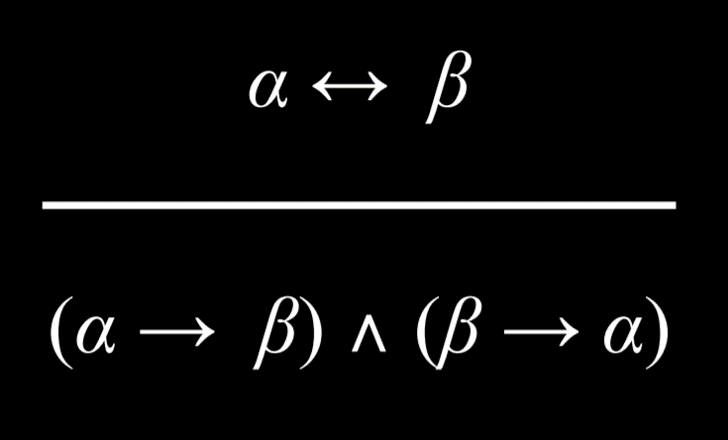
|
等值命题等价于蕴涵及其逆命题的 And 关系。例如,“当且仅当 Harry 在室内时才下雨”等同于 (“如果正在下雨,Harry 在室内”和“如果 Harry 在室内,则正在下雨”)。
|
||||||
|
|
||||||
- 德摩根律 (De Morgan’s Law)
|
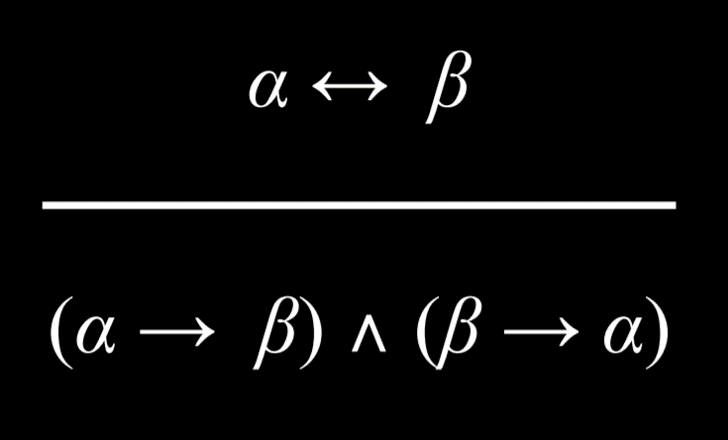
|
||||||
|
|
||||||
- 可以将 And 连接词变成 Or 连接词。考虑以下命题:“哈利和罗恩都通过了考试是不正确的。”由此,可以得出“哈利通过考试不是真的”或者“罗恩不是真的通过考试”的结论。也就是说,要使前面的 And 命题为真,Or 命题中至少有一个命题必须为真。
|
#### 德摩根律 (De Morgan’s Law)
|
||||||
|
|
||||||
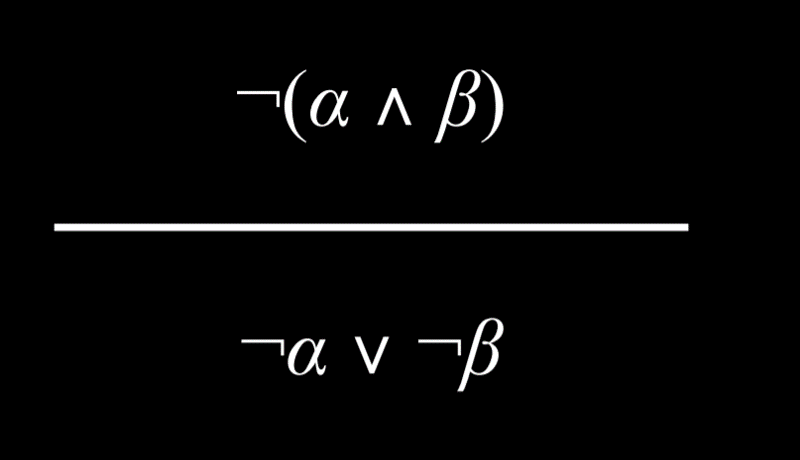
|
可以将 And 连接词变成 Or 连接词。考虑以下命题:“哈利和罗恩都通过了考试是不正确的。”由此,可以得出“哈利通过考试不是真的”或者“罗恩不是真的通过考试”的结论。也就是说,要使前面的 And 命题为真,Or 命题中至少有一个命题必须为真。
|
||||||
|
|
||||||
- 同样,可以得出相反的结论。考虑这个命题“哈利或罗恩通过考试是不正确的”。这可以改写为“哈利没有通过考试”和“罗恩没有通过考试”。
|
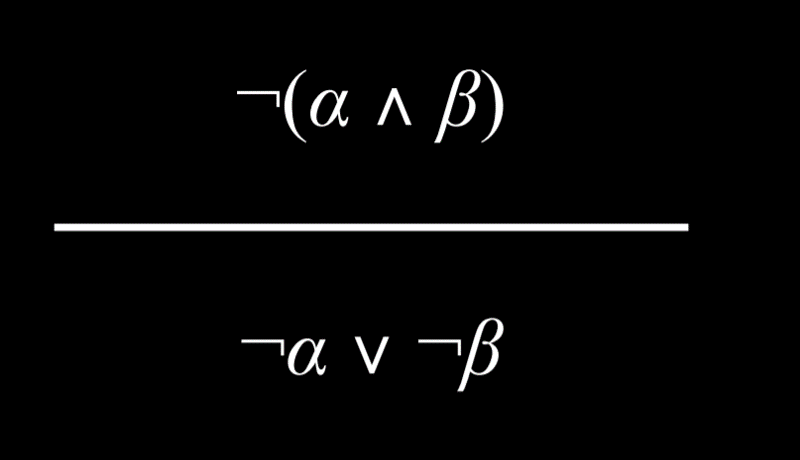
|
||||||
|
|
||||||
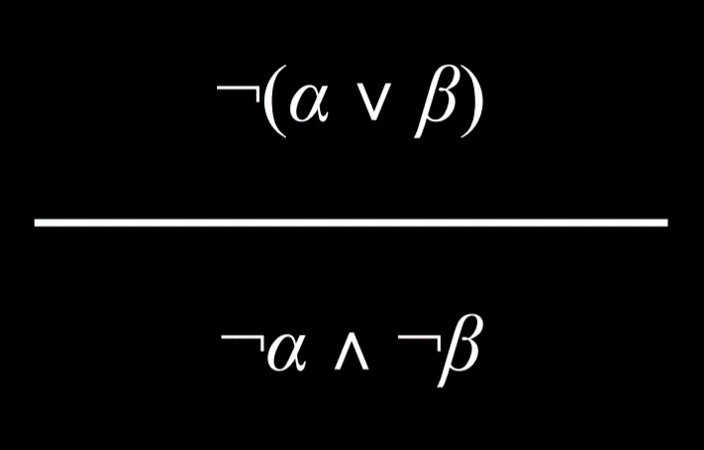
|
同样,可以得出相反的结论。考虑这个命题“哈利或罗恩通过考试是不正确的”。这可以改写为“哈利没有通过考试”和“罗恩没有通过考试”。
|
||||||
|
|
||||||
- 分配律 (Distributive Property)
|
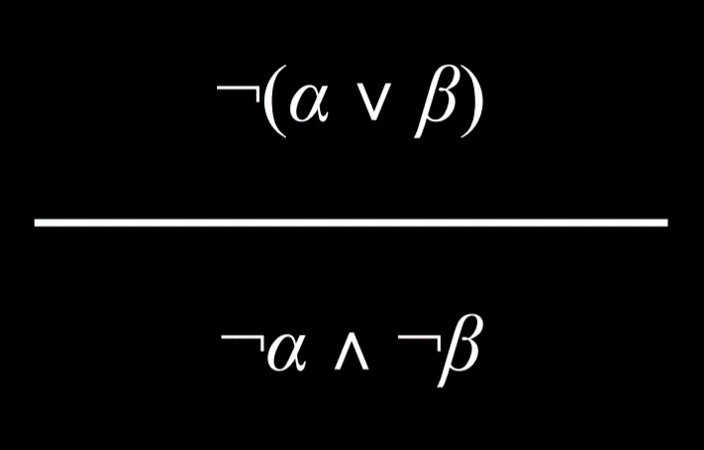
|
||||||
|
|
||||||
- 具有两个用 And 或 Or 连接词分组的命题可以分解为由 And 和 Or 组成的更小单元。
|
#### 分配律 (Distributive Property)
|
||||||
|
|
||||||
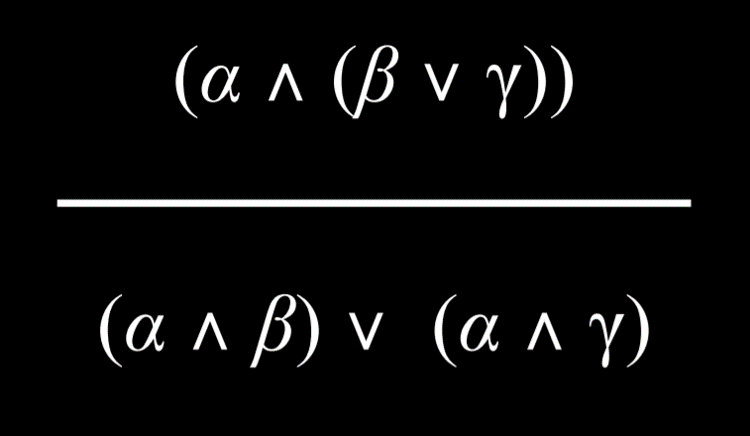
|
具有两个用 And 或 Or 连接词分组的命题可以分解为由 And 和 Or 组成的更小单元。
|
||||||
|
|
||||||
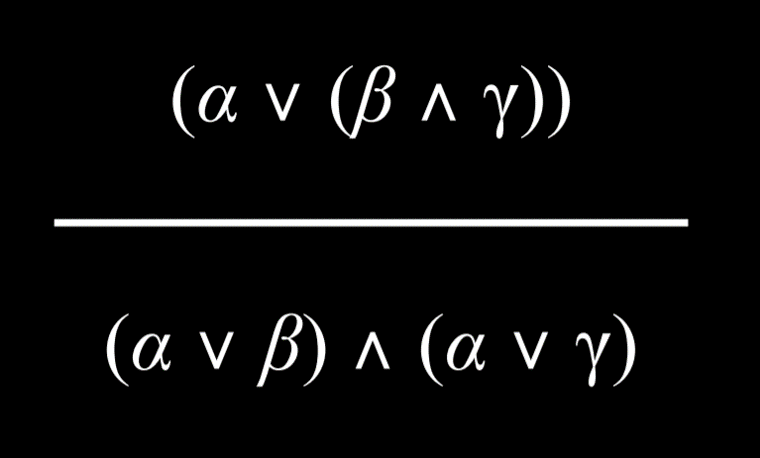
|
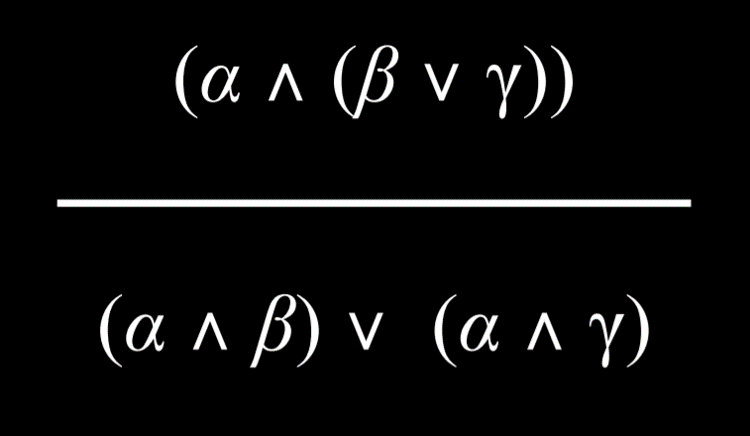
|
||||||
|
|
||||||
|
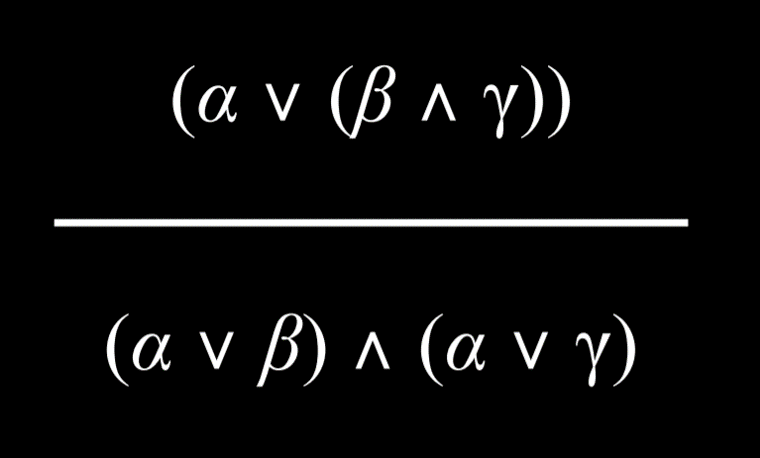
|
||||||
|
|
||||||
### 知识和搜索问题
|
### 知识和搜索问题
|
||||||
|
|
||||||
- 推理可以被视为具有以下属性的搜索问题:
|
推理可以被视为具有以下属性的搜索问题:
|
||||||
|
|
||||||
- 初始状态:知识库
|
- 初始状态:知识库
|
||||||
- 动作:推理规则
|
- 动作:推理规则
|
||||||
- 过渡模型:推理后的新知识库
|
- 过渡模型:推理后的新知识库
|
||||||
- 目标测试:检查我们要证明的语句是否在知识库中
|
- 目标测试:检查我们要证明的语句是否在知识库中
|
||||||
- 路径成本:证明中的步骤数
|
- 路径成本:证明中的步骤数
|
||||||
- 这显示了搜索算法的通用性,使我们能够使用推理规则根据现有知识推导出新信息。
|
|
||||||
|
这显示了搜索算法的通用性,使我们能够使用推理规则根据现有知识推导出新信息。
|
||||||
|
|
||||||
## 归结 (Resolution)
|
## 归结 (Resolution)
|
||||||
|
|
||||||
- 归结是一个强大的推理规则,它规定如果 Or 命题中的两个原子命题之一为假,则另一个必须为真。例如,给定命题“Ron 在礼堂”或“Hermione 在图书馆”,除了命题“Ron 不在礼堂”之外,我们还可以得出“Hermione 在图书馆”的结论。更正式地说,我们可以通过以下方式定义归结:
|
归结是一个强大的推理规则,它规定如果 Or 命题中的两个原子命题之一为假,则另一个必须为真。例如,给定命题“Ron 在礼堂”或“Hermione 在图书馆”,除了命题“Ron 不在礼堂”之外,我们还可以得出“Hermione 在图书馆”的结论。更正式地说,我们可以通过以下方式定义归结:
|
||||||
|
|
||||||
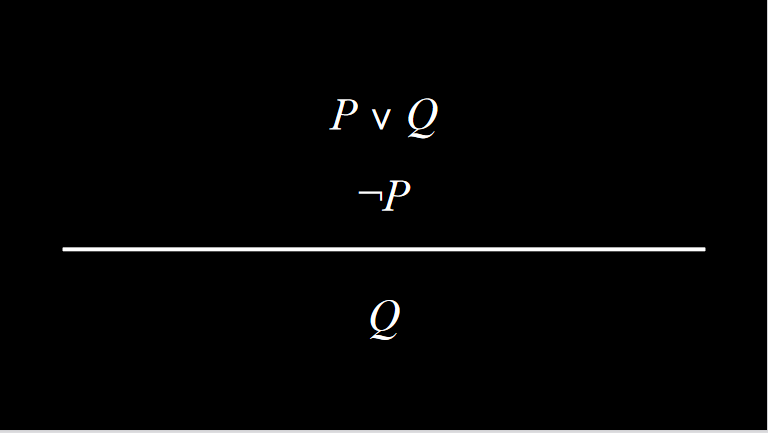
|
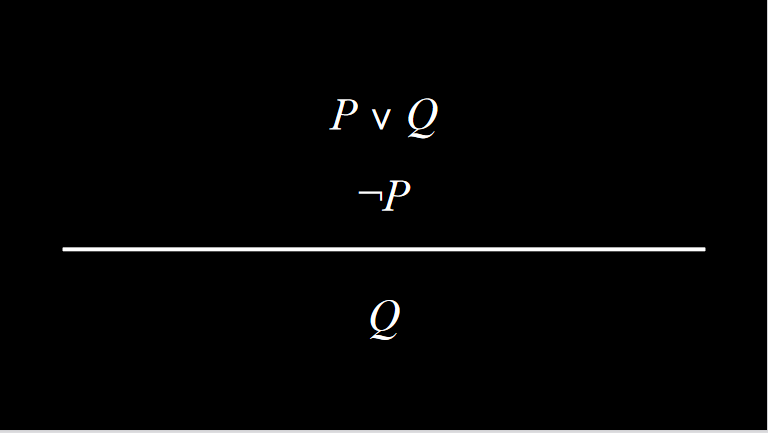
|
||||||
|
|
||||||
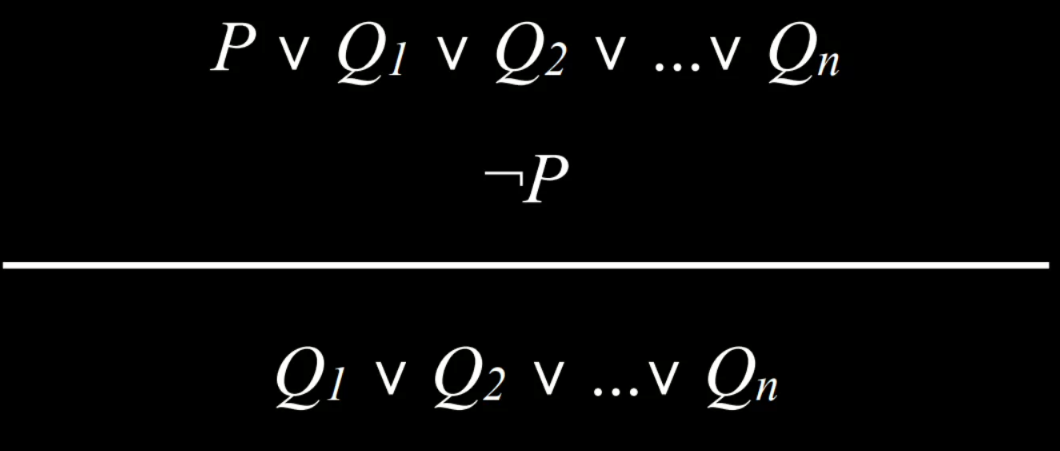
|
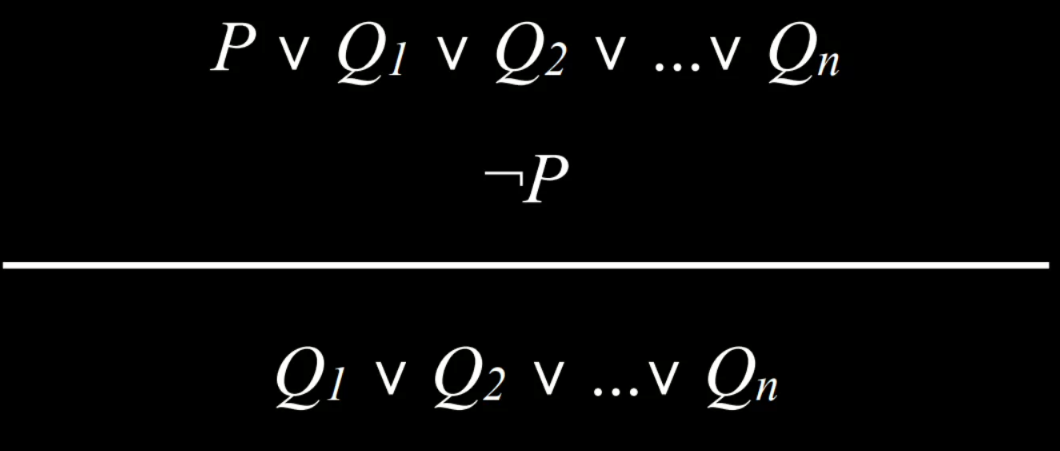
|
||||||
|
|
||||||
- 归结依赖于互补文字,两个相同的原子命题,其中一个被否定而另一个不被否定,例如$P$和$¬P$。
|
归结依赖于互补文字,两个相同的原子命题,其中一个被否定而另一个不被否定,例如$P$和$¬P$。
|
||||||
- 归结可以进一步推广。假设除了“Rom 在礼堂”或“Hermione 在图书馆”的命题外,我们还知道“Rom 不在礼堂”或“Harry 在睡觉”。我们可以从中推断出“Hermione 在图书馆”或“Harry 在睡觉”。正式地说:
|
|
||||||
|
|
||||||

|
归结可以进一步推广。假设除了“Rom 在礼堂”或“Hermione 在图书馆”的命题外,我们还知道“Rom 不在礼堂”或“Harry 在睡觉”。我们可以从中推断出“Hermione 在图书馆”或“Harry 在睡觉”。正式地说:
|
||||||
|
|
||||||
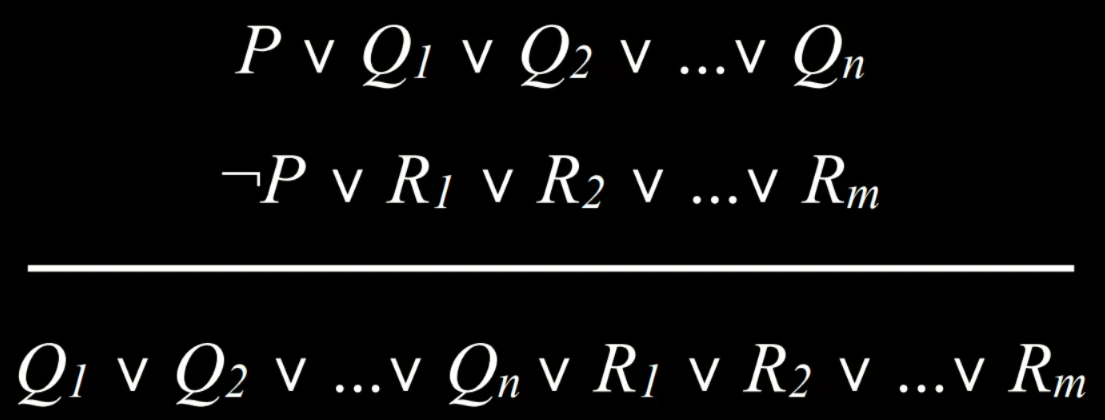
|

|
||||||
|
|
||||||
- 互补文字使我们能够通过解析推理生成新句子。因此,推理算法定位互补文字以生成新知识。
|
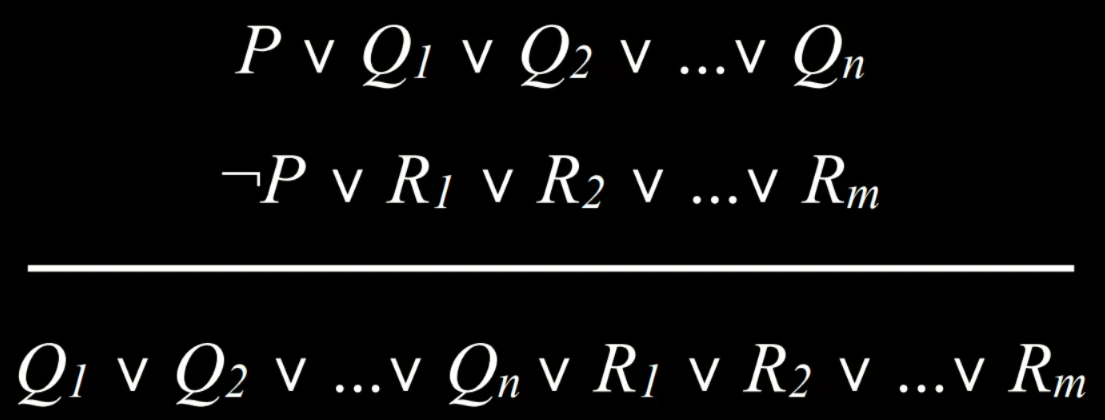
|
||||||
- 从句 (Clause) 是多个原子命题的析取式(命题符号或命题符号的否定,例如$P$, $¬P$)。析取式由 Or 逻辑连接词 ($P ∨ Q ∨ R$) 相连的命题组成。另一方面,连接词由 And 逻辑连接词 ($P ∧ Q ∧ R$) 相连的命题组成。从句允许我们将任何逻辑语句转换为合取范式 (CNF),它是从句的合取,例如:$(A ∨ B ∨ C) ∧ (D ∨ ¬E) ∧ (F ∨ G)$。
|
|
||||||
- 命题转换为合取范式的步骤、
|
|
||||||
|
|
||||||
- 等值消除
|
互补文字使我们能够通过解析推理生成新句子。因此,推理算法定位互补文字以生成新知识。
|
||||||
|
|
||||||
- 将$(α↔ β)$转化为$(α→ β)∧ (β → α)$
|
从句 (Clause) 是多个原子命题的析取式(命题符号或命题符号的否定,例如$P$, $¬P$)。析取式由 Or 逻辑连接词 ($P ∨ Q ∨ R$) 相连的命题组成。另一方面,连接词由 And 逻辑连接词 ($P ∧ Q ∧ R$) 相连的命题组成。从句允许我们将任何逻辑语句转换为合取范式 (CNF),它是从句的合取,例如:$(A ∨ B ∨ C) ∧ (D ∨ ¬E) ∧ (F ∨ G)$。
|
||||||
- 蕴含消除
|
|
||||||
|
|
||||||
|
命题转换为合取范式的步骤、
|
||||||
|
|
||||||
|
1. 等值消除
|
||||||
|
- 将$(α↔ β)$转化为$(α→ β)∧ (β → α)$
|
||||||
|
2. 蕴含消除
|
||||||
- 将$(α→ β)$转化为$\lnotα∧β$
|
- 将$(α→ β)$转化为$\lnotα∧β$
|
||||||
- 使用德摩根定律,将否定向内移动,直到只有原子命题被否定(而不是从句)
|
3. 使用德摩根定律,将否定向内移动,直到只有原子命题被否定(而不是从句)
|
||||||
|
- 将$\lnot(\alpha∧β)$转换为$\lnotα\lor\lnotβ$
|
||||||
- 将$\lnot(\alpha∧β)$转换为$\lnotα\lor\lnotβ$
|
4. 下面是一个转换$(P∧Q)\to R$到合取范式的例子:
|
||||||
- 下面是一个转换$(P∧Q)\to R$到合取范式的例子:
|
|
||||||
|
|
||||||
- $(P ∨ Q) → R$
|
- $(P ∨ Q) → R$
|
||||||
- $\lnot(P\lor Q)\lor R$蕴含消除
|
- $\lnot(P\lor Q)\lor R$蕴含消除
|
||||||
- $(\lnot P\land\lnot Q)\lor R$德摩根律
|
- $(\lnot P\land\lnot Q)\lor R$德摩根律
|
||||||
- $(\lnot P\lor R)\land(\lnot Q\lor R)$分配律
|
- $(\lnot P\lor R)\land(\lnot Q\lor R)$分配律
|
||||||
- 归结命题及其否定,即$\lnot P$和$P$,得到空从句$()$。空从句总是假的,这是有道理的,因为$P$和$\lnot P$ 不可能都是真的。归结算法使用了这个事实。
|
|
||||||
|
|
||||||
- 确定是否$KB⊨α$:
|
归结命题及其否定,即$\lnot P$和$P$,得到空从句$()$。空从句总是假的,这是有道理的,因为$P$和$\lnot P$ 不可能都是真的。归结算法使用了这个事实。
|
||||||
|
|
||||||
- 检查:$(KB∧\lnotα)$是矛盾的吗?
|
- 确定是否$KB⊨α$:
|
||||||
|
- 检查:$(KB∧\lnotα)$是矛盾的吗?
|
||||||
|
- 如果是这样,那么$KB⊨α$。
|
||||||
|
- 否则,$KB$无法蕴含推理出$\alpha$。
|
||||||
|
|
||||||
- 如果是这样,那么$KB⊨α$。
|
矛盾证明是计算机科学中经常使用的一种工具。如果我们的知识库是真的,并且它与$\lnot α$相矛盾,那就意味着$\lnot\alpha$是假的,因此$α$必须是真的。从技术上讲,该算法将执行以下操作:
|
||||||
- 否则,$KB$无法蕴含推理出$\alpha$。
|
|
||||||
- 矛盾证明是计算机科学中经常使用的一种工具。如果我们的知识库是真的,并且它与$\lnot α$相矛盾,那就意味着$\lnot\alpha$是假的,因此$α$必须是真的。从技术上讲,该算法将执行以下操作:
|
|
||||||
|
|
||||||
- 确定是否$KB⊨α$:
|
- 确定是否$KB⊨α$:
|
||||||
- 将$(KB∧\lnotα)$转换为合取范式。
|
- 将$(KB∧\lnotα)$转换为合取范式。
|
||||||
- 继续检查,看看我们是否可以使用归结来生成一个新的从句。
|
- 继续检查,看看我们是否可以使用归结来生成一个新的从句。
|
||||||
- 如果我们生成了空从句(相当于 False),那么恭喜你!我们得出了一个矛盾,从而证明了$KB⊨α$。
|
- 如果我们生成了空从句(相当于 False),那么恭喜你!我们得出了一个矛盾,从而证明了$KB⊨α$。
|
||||||
- 然而,如果没有实现矛盾,并且不能推断出更多的从句,那么就没有蕴含性。
|
- 然而,如果没有实现矛盾,并且不能推断出更多的从句,那么就没有蕴含性。
|
||||||
- 以下是一个示例,说明了该算法的工作原理:
|
- 以下是一个示例,说明了该算法的工作原理:
|
||||||
- $(A ∨ B) ∧ (¬B ∨ C) ∧ (¬C)\vDash A?$
|
- $(A ∨ B) ∧ (¬B ∨ C) ∧ (¬C)\vDash A?$
|
||||||
- $(A ∨ B) ∧ (¬B ∨ C) ∧ (¬C) ∧ (¬A)$
|
- $(A ∨ B) ∧ (¬B ∨ C) ∧ (¬C) ∧ (¬A)$
|
||||||
- $(\lnot B\lor C)\land\lnot C\vDash\lnot B\implies(A ∨ B) ∧ (¬B ∨ C) ∧ (¬C) ∧ (¬A)\land (\lnot B)$
|
- $(\lnot B\lor C)\land\lnot C\vDash\lnot B\implies(A ∨ B) ∧ (¬B ∨ C) ∧ (¬C) ∧ (¬A)\land (\lnot B)$
|
||||||
- $(A\lor B)\land\lnot B\vDash A\implies(A ∨ B) ∧ (¬B ∨ C) ∧ (¬C) ∧ (¬A)\land (\lnot B)\land(A)$
|
- $(A\lor B)\land\lnot B\vDash A\implies(A ∨ B) ∧ (¬B ∨ C) ∧ (¬C) ∧ (¬A)\land (\lnot B)\land(A)$
|
||||||
- $(\lnot A\land A)\vDash ()\implies(A ∨ B) ∧ (¬B ∨ C) ∧ (¬C) ∧ (¬A)\land (\lnot B)\land(A)\land ()\implies False$
|
- $(\lnot A\land A)\vDash ()\implies(A ∨ B) ∧ (¬B ∨ C) ∧ (¬C) ∧ (¬A)\land (\lnot B)\land(A)\land ()\implies False$
|
||||||
|
|
||||||
## 一阶逻辑 (First Order Logic)
|
## 一阶逻辑 (First Order Logic)
|
||||||
|
|
||||||
- 一阶逻辑是另一种类型的逻辑,它使我们能够比命题逻辑更简洁地表达更复杂的想法。一阶逻辑使用两种类型的符号:常量符号和谓词符号。常量符号表示对象,而谓词符号类似于接受参数并返回 true 或 false 值的关系或函数。
|
一阶逻辑是另一种类型的逻辑,它使我们能够比命题逻辑更简洁地表达更复杂的想法。一阶逻辑使用两种类型的符号:常量符号和谓词符号。常量符号表示对象,而谓词符号类似于接受参数并返回 true 或 false 值的关系或函数。
|
||||||
- 例如,我们回到霍格沃茨不同的人和家庭作业的逻辑谜题。常量符号是指人或房子,如 Minerva、Pomona、Gryffindor、Hufflepuff 等。谓语符号是一些常量符号的真或虚的属性。例如,我们可以使用句子 `person(Minerva)` 来表达 Minerva 是一个人的想法。同样,我们可以用 `house(Gryffindor)` 这个句子来表达 Gryffindor 是一所房子的想法。所有的逻辑连接词都以与以前相同的方式在一阶逻辑中工作。例如,$\lnot$`House(Minerva)` 表达了 Minerva 不是房子的想法。谓词符号也可以接受两个或多个自变量,并表达它们之间的关系。例如,BelongsTo 表达了两个论点之间的关系,即人和人所属的房子。因此,Minerva 拥有 Gryffindor 的想法可以表达为 `BelongsTo(Minerva,Gryffindor)`。一阶逻辑允许每个人一个符号,每个房子一个符号。这比命题逻辑更简洁,因为命题逻辑中每个人的房屋分配都需要不同的符号。
|
|
||||||
- 全称量化 (Universal Quantification)
|
|
||||||
|
|
||||||
- 量化是一种可以在一阶逻辑中使用的工具,可以在不使用特定常量符号的情况下表示句子。全称量化使用符号$∀$来表示“所有”。例如,$\forall x(BelongsTo(x, Gryffindor) → ¬BelongsTo(x, Hufflepuff))$表达了这样一种观点,即对于每个符号来说,如果这个符号属于 Gryffindor,那么它就不属于 Hufflepuff。
|
例如,我们回到霍格沃茨不同的人和家庭作业的逻辑谜题。常量符号是指人或房子,如 Minerva、Pomona、Gryffindor、Hufflepuff 等。谓语符号是一些常量符号的真或虚的属性。例如,我们可以使用句子 `person(Minerva)` 来表达 Minerva 是一个人的想法。同样,我们可以用 `house(Gryffindor)` 这个句子来表达 Gryffindor 是一所房子的想法。所有的逻辑连接词都以与以前相同的方式在一阶逻辑中工作。例如,$\lnot$`House(Minerva)` 表达了 Minerva 不是房子的想法。谓词符号也可以接受两个或多个自变量,并表达它们之间的关系。例如,BelongsTo 表达了两个论点之间的关系,即人和人所属的房子。因此,Minerva 拥有 Gryffindor 的想法可以表达为 `BelongsTo(Minerva,Gryffindor)`。一阶逻辑允许每个人一个符号,每个房子一个符号。这比命题逻辑更简洁,因为命题逻辑中每个人的房屋分配都需要不同的符号。
|
||||||
- 存在量化 (Existential Quantification)
|
|
||||||
|
|
||||||
- 存在量化是一个与全称量化平行的概念。然而,虽然全称量化用于创建对所有$x$都成立的句子,但存在量化用于创建至少对一个$x$成立的句子。它使用符号$∃$表示。例如,$∃x(House(x) ∧ BelongsTo(Minerva, x))$ 意味着至少有一个符号既是房子,又是属于 Minerva。换句话说,这表达了 Minerva 拥有房子的想法。
|
### 全称量化 (Universal Quantification)
|
||||||
- 存在量化和全称量化可以用在同一个句子中。例如,$∀x(Person(x) → (∃y(House(y) ∧ BelongsTo(x, y))))$表达了这样一种观点,即如果$x$是一个人,那么这个人至少拥有一个房子$y$。换句话说,这句话的意思是每个人都拥有一所房子。
|
|
||||||
|
量化是一种可以在一阶逻辑中使用的工具,可以在不使用特定常量符号的情况下表示句子。全称量化使用符号$∀$来表示“所有”。例如,$\forall x(BelongsTo(x, Gryffindor) → ¬BelongsTo(x, Hufflepuff))$表达了这样一种观点,即对于每个符号来说,如果这个符号属于 Gryffindor,那么它就不属于 Hufflepuff。
|
||||||
|
|
||||||
|
### 存在量化 (Existential Quantification)
|
||||||
|
|
||||||
|
存在量化是一个与全称量化平行的概念。然而,虽然全称量化用于创建对所有$x$都成立的句子,但存在量化用于创建至少对一个$x$成立的句子。它使用符号$∃$表示。例如,$∃x(House(x) ∧ BelongsTo(Minerva, x))$ 意味着至少有一个符号既是房子,又是属于 Minerva。换句话说,这表达了 Minerva 拥有房子的想法。
|
||||||
|
|
||||||
|
存在量化和全称量化可以用在同一个句子中。例如,$∀x(Person(x) → (∃y(House(y) ∧ BelongsTo(x, y))))$表达了这样一种观点,即如果$x$是一个人,那么这个人至少拥有一个房子$y$。换句话说,这句话的意思是每个人都拥有一所房子。
|
||||||
|
|
||||||
还有其他类型的逻辑,它们之间的共同点是,它们都是为了表示信息而存在的。这些是我们用来在人工智能中表示知识的系统。
|
还有其他类型的逻辑,它们之间的共同点是,它们都是为了表示信息而存在的。这些是我们用来在人工智能中表示知识的系统。
|
||||||
|
|
||||||
|
|||||||
@@ -12,71 +12,87 @@
|
|||||||
|
|
||||||
## 背景
|
## 背景
|
||||||
|
|
||||||
- GJB2 基因的突变版本是导致新生儿听力障碍的主要原因之一。每个人都携带两个版本的基因,因此每个人都有可能拥有 0、1 或 2 个听力障碍版本的 GJB2 基因。不过,除非一个人接受基因测试,否则要知道一个人拥有多少个变异的 GJB2 基因并不那么容易。这是一些 "隐藏状态":具有我们可以观察到的影响(听力损伤)的信息,但我们不一定直接知道。毕竟,有些人可能有 1 或 2 个突变的 GJB2 基因,但没有表现出听力障碍,而其他人可能没有突变的 GJB2 基因,但仍然表现出听力障碍。
|
GJB2 基因的突变版本是导致新生儿听力障碍的主要原因之一。每个人都携带两个版本的基因,因此每个人都有可能拥有 0、1 或 2 个听力障碍版本的 GJB2 基因。不过,除非一个人接受基因测试,否则要知道一个人拥有多少个变异的 GJB2 基因并不那么容易。这是一些 "隐藏状态":具有我们可以观察到的影响(听力损伤)的信息,但我们不一定直接知道。毕竟,有些人可能有 1 或 2 个突变的 GJB2 基因,但没有表现出听力障碍,而其他人可能没有突变的 GJB2 基因,但仍然表现出听力障碍。
|
||||||
- 每个孩子都会从他们的父母那里继承一个 GJB2 基因。如果父母有两个变异基因,那么他们会将变异基因传给孩子;如果父母没有变异基因,那么他们不会将变异基因传给孩子;如果父母有一个变异基因,那么该基因传给孩子的概率为 0.5。不过,在基因被传递后,它有一定的概率发生额外的突变:从导致听力障碍的基因版本转变为不导致听力障碍的版本,或者反过来。
|
|
||||||
- 我们可以尝试通过对所有相关变量形成一个贝叶斯网络来模拟所有这些关系,就像下面这个网络一样,它考虑了一个由两个父母和一个孩子组成的家庭。
|
每个孩子都会从他们的父母那里继承一个 GJB2 基因。如果父母有两个变异基因,那么他们会将变异基因传给孩子;如果父母没有变异基因,那么他们不会将变异基因传给孩子;如果父母有一个变异基因,那么该基因传给孩子的概率为 0.5。不过,在基因被传递后,它有一定的概率发生额外的突变:从导致听力障碍的基因版本转变为不导致听力障碍的版本,或者反过来。
|
||||||
|
|
||||||
|
我们可以尝试通过对所有相关变量形成一个贝叶斯网络来模拟所有这些关系,就像下面这个网络一样,它考虑了一个由两个父母和一个孩子组成的家庭。
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
- 家庭中的每个人都有一个 `Gene` 随机变量,代表一个人有多少个特定基因(例如,GJB2 的听力障碍版本):一个 0、1 或 2 的值。家族中的每个人也有一个 `Trait` 随机变量,它是 `yes` 或 `no`,取决于该人是否表达基于该基因的性状(例如,听力障碍)。从每个人的 `Gene` 变量到他们的 `Trait` 变量之间有一个箭头,以编码一个人的基因影响他们具有特定性状的概率的想法。同时,也有一个箭头从母亲和父亲的 `Gene` 随机变量到他们孩子的 `Gene` 随机变量:孩子的基因取决于他们父母的基因。
|
家庭中的每个人都有一个 `Gene` 随机变量,代表一个人有多少个特定基因(例如,GJB2 的听力障碍版本):一个 0、1 或 2 的值。家族中的每个人也有一个 `Trait` 随机变量,它是 `yes` 或 `no`,取决于该人是否表达基于该基因的性状(例如,听力障碍)。从每个人的 `Gene` 变量到他们的 `Trait` 变量之间有一个箭头,以编码一个人的基因影响他们具有特定性状的概率的想法。同时,也有一个箭头从母亲和父亲的 `Gene` 随机变量到他们孩子的 `Gene` 随机变量:孩子的基因取决于他们父母的基因。
|
||||||
- 你在这个项目中的任务是使用这个模型对人群进行推断。给出人们的信息,他们的父母是谁,以及他们是否具有由特定基因引起的特定可观察特征(如听力损失),你的人工智能将推断出每个人的基因的概率分布,以及任何一个人是否会表现出有关特征的概率分布。
|
|
||||||
|
你在这个项目中的任务是使用这个模型对人群进行推断。给出人们的信息,他们的父母是谁,以及他们是否具有由特定基因引起的特定可观察特征(如听力损失),你的人工智能将推断出每个人的基因的概率分布,以及任何一个人是否会表现出有关特征的概率分布。
|
||||||
|
|
||||||
## 理解
|
## 理解
|
||||||
|
|
||||||
- 打开 `data/family0.csv`,看看数据目录中的一个样本数据集(你可以在文本编辑器中打开,或者在 Google Sheets、Excel 或 Apple Numbers 等电子表格应用程序中打开)。注意,第一行定义了这个 CSV 文件的列:`name`, `mother`, `father`, 和 `trait`。下一行表明 Harry 的母亲是 Lily,父亲是 James,而 `Trait` 的空单元格意味着我们不知道 Harry 是否有这种性状。同时,James 在我们的数据集中没有列出父母(如母亲和父亲的空单元格所示),但确实表现出了性状(如 `Trait` 单元格中的 1 所示)。另一方面,Lily 在数据集中也没有列出父母,但没有表现出这种性状(如 `Trait` 单元格中的 0 表示)。
|
打开 `data/family0.csv`,看看数据目录中的一个样本数据集(你可以在文本编辑器中打开,或者在 Google Sheets、Excel 或 Apple Numbers 等电子表格应用程序中打开)。注意,第一行定义了这个 CSV 文件的列:`name`, `mother`, `father`, 和 `trait`。下一行表明 Harry 的母亲是 Lily,父亲是 James,而 `Trait` 的空单元格意味着我们不知道 Harry 是否有这种性状。同时,James 在我们的数据集中没有列出父母(如母亲和父亲的空单元格所示),但确实表现出了性状(如 `Trait` 单元格中的 1 所示)。另一方面,Lily 在数据集中也没有列出父母,但没有表现出这种性状(如 `Trait` 单元格中的 0 表示)。
|
||||||
- 打开 `heredity.py`,首先看一下 `PROBS` 的定义。`PROBS` 是一个包含若干常数的字典,代表各种不同事件的概率。所有这些事件都与一个人拥有多少个特定的突变基因,以及一个人是否基于该基因表现出特定的性状有关。这里的数据松散地基于 GJB2 基因的听力障碍版本和听力障碍性状的概率,但通过改变这些值,你也可以用你的人工智能来推断其他的基因和性状!
|
|
||||||
- 首先,`PROBS["gene"]` 代表了该基因的无条件概率分布(即如果我们对该人的父母一无所知的概率)。根据分布代码中的数据,在人群中,有 1% 的机会拥有该基因的 2 个副本,3% 的机会拥有该基因的 1 个副本,96% 的机会拥有该基因的零副本。
|
打开 `heredity.py`,首先看一下 `PROBS` 的定义。`PROBS` 是一个包含若干常数的字典,代表各种不同事件的概率。所有这些事件都与一个人拥有多少个特定的突变基因,以及一个人是否基于该基因表现出特定的性状有关。这里的数据松散地基于 GJB2 基因的听力障碍版本和听力障碍性状的概率,但通过改变这些值,你也可以用你的人工智能来推断其他的基因和性状!
|
||||||
- 接下来,`PROBS["trait"]` 表示一个人表现出某种性状(如听力障碍)的条件概率。这实际上是三个不同的概率分布:基因的每个可能值都有一个。因此,`PROBS["trait"][2]` 是一个人在有两个突变基因的情况下具有该特征的概率分布:在这种情况下,他们有 65% 的机会表现出该特征,而有 35% 的机会不表现出该特征。同时,如果一个人有 0 个变异基因,他们有 1% 的机会表现出该性状,99% 的机会不表现出该性状。
|
|
||||||
- 最后,`PROBS["mutation"]` 是一个基因从作为相关基因突变为不是该基因的概率,反之亦然。例如,如果一个母亲有两个变异基因,并因此将其中一个传给她的孩子,就有 1% 的机会突变为不再是变异基因。相反,如果一个母亲没有任何变异基因,因此没有把变异基因传给她的孩子,但仍有 1% 的机会突变为变异基因。因此,即使父母双方都没有变异基因,他们的孩子也可能有 1 个甚至 2 个变异基因。
|
首先,`PROBS["gene"]` 代表了该基因的无条件概率分布(即如果我们对该人的父母一无所知的概率)。根据分布代码中的数据,在人群中,有 1% 的机会拥有该基因的 2 个副本,3% 的机会拥有该基因的 1 个副本,96% 的机会拥有该基因的零副本。
|
||||||
- 最终,你计算的概率将以 `PROBS` 中的这些数值为基础。
|
|
||||||
- 现在,看一下 `main` 函数。该函数首先将数据从一个文件加载到一个字典 `people` 中。`people` 将每个人的名字映射到另一个包含他们信息的字典中:包括他们的名字,他们的母亲(如果数据集中有一个母亲),他们的父亲(如果数据集中有一个父亲),以及他们是否被观察到有相关的特征(如果有则为 `True`,没有则为 `False`,如果我们不知道则为 `None`)。
|
接下来,`PROBS["trait"]` 表示一个人表现出某种性状(如听力障碍)的条件概率。这实际上是三个不同的概率分布:基因的每个可能值都有一个。因此,`PROBS["trait"][2]` 是一个人在有两个突变基因的情况下具有该特征的概率分布:在这种情况下,他们有 65% 的机会表现出该特征,而有 35% 的机会不表现出该特征。同时,如果一个人有 0 个变异基因,他们有 1% 的机会表现出该性状,99% 的机会不表现出该性状。
|
||||||
- 接下来,`main` 中定义了一个字典 `probabilities`,所有的概率最初都设置为 0。这就是你的项目最终要计算的内容:对于每个人,你的人工智能将计算他们有多少个变异基因的概率分布,以及他们是否具有该性状。例如,`probabilities["Harry"]["gene"][1]` 将是 Harry 有 1 个变异基因的概率,而 `probabilities["Lily"]["trait"][False]` 将是 Lily 没有表现出该性状的概率。
|
|
||||||
- 如果不熟悉的话,这个 `probabilities` 字典是用 [python 字典](https://www.python.org/dev/peps/pep-0274/)创建的,在这种情况下,它为我们的 `people` 中的每个 `person` 创建一个键/值对。
|
最后,`PROBS["mutation"]` 是一个基因从作为相关基因突变为不是该基因的概率,反之亦然。例如,如果一个母亲有两个变异基因,并因此将其中一个传给她的孩子,就有 1% 的机会突变为不再是变异基因。相反,如果一个母亲没有任何变异基因,因此没有把变异基因传给她的孩子,但仍有 1% 的机会突变为变异基因。因此,即使父母双方都没有变异基因,他们的孩子也可能有 1 个甚至 2 个变异基因。
|
||||||
- 最终,我们希望根据一些证据来计算这些概率:鉴于我们知道某些人有或没有这种特征,我们想确定这些概率。你在这个项目中的任务是实现三个函数来做到这一点: `joint_probability` 计算一个联合概率,`update` 将新计算的联合概率添加到现有的概率分布中,然后 `normalize` 以确保所有概率分布最后和为 1。
|
|
||||||
|
最终,你计算的概率将以 `PROBS` 中的这些数值为基础。
|
||||||
|
|
||||||
|
现在,看一下 `main` 函数。该函数首先将数据从一个文件加载到一个字典 `people` 中。`people` 将每个人的名字映射到另一个包含他们信息的字典中:包括他们的名字,他们的母亲(如果数据集中有一个母亲),他们的父亲(如果数据集中有一个父亲),以及他们是否被观察到有相关的特征(如果有则为 `True`,没有则为 `False`,如果我们不知道则为 `None`)。
|
||||||
|
接下来,`main` 中定义了一个字典 `probabilities`,所有的概率最初都设置为 0。这就是你的项目最终要计算的内容:对于每个人,你的人工智能将计算他们有多少个变异基因的概率分布,以及他们是否具有该性状。例如,`probabilities["Harry"]["gene"][1]` 将是 Harry 有 1 个变异基因的概率,而 `probabilities["Lily"]["trait"][False]` 将是 Lily 没有表现出该性状的概率。
|
||||||
|
|
||||||
|
如果不熟悉的话,这个 `probabilities` 字典是用 [python 字典](https://www.python.org/dev/peps/pep-0274/)创建的,在这种情况下,它为我们的 `people` 中的每个 `person` 创建一个键/值对。
|
||||||
|
|
||||||
|
最终,我们希望根据一些证据来计算这些概率:鉴于我们知道某些人有或没有这种特征,我们想确定这些概率。你在这个项目中的任务是实现三个函数来做到这一点: `joint_probability` 计算一个联合概率,`update` 将新计算的联合概率添加到现有的概率分布中,然后 `normalize` 以确保所有概率分布最后和为 1。
|
||||||
|
|
||||||
## 明确
|
## 明确
|
||||||
|
|
||||||
- 完成 `joint_probability`、`update` 和 `normalize` 的实现。
|
完成 `joint_probability`、`update` 和 `normalize` 的实现。
|
||||||
- `joint_probability` 函数应该接受一个 `people` 的字典作为输入,以及关于谁拥有多少个变异基因,以及谁表现出该特征的数据。该函数应该返回所有这些事件发生的联合概率。
|
|
||||||
|
|
||||||
- 该函数接受四个数值作为输入:`people`, `one_gene`, `two_genes`, 和 `have_trait`。
|
`joint_probability` 函数应该接受一个 `people` 的字典作为输入,以及关于谁拥有多少个变异基因,以及谁表现出该特征的数据。该函数应该返回所有这些事件发生的联合概率。
|
||||||
|
|
||||||
- `people` 是一个在 "理解"一节中描述的人的字典。键代表名字,值是包含 `mother` 和 `father` 键的字典。你可以假设 `mother` 和 `father` 都是空白的(数据集中没有父母的信息),或者 `mother` 和 `father` 都会指代 `people` 字典中的其他人物。
|
- 该函数接受四个数值作为输入:`people`, `one_gene`, `two_genes`, 和 `have_trait`。
|
||||||
- `one_gene` 是一个集合,我们想计算所有集合元素有一个变异基因的概率。
|
|
||||||
- `two_genes` 是一个集合,我们想计算所有集合元素有两个变异基因的概率。
|
|
||||||
- `have_trait` 是一个集合,我们想计算所有集合元素拥有该性状的概率。
|
|
||||||
- 对于不在 `one_gene` 或 t `wo_genes` 中的人,我们想计算他们没有变异基因的概率;对于不在 `have_trait` 中的人,我们想计算他们没有该性状的概率。
|
|
||||||
|
|
||||||
- 例如,如果这个家庭由 Harry、James 和 Lily 组成,那么在 `one_gene = {"Harry"}`、`two_genes = {"James"}` 和 `trait = {"Harry"、"James"}` 的情况下调用这个函数,应该计算出 Lily 没有变异基因、Harry 拥有一个变异基因、James 拥有两个变异基因、Harry 表现出该性状、James 表现出该性状和 Lily 没有表现出该性状的联合概率。
|
|
||||||
- 对于数据集中没有列出父母的人,使用概率分布 `PROBS["gene"]` 来确定他们有特定数量基因的概率。
|
|
||||||
- 对于数据集中有父母的人来说,每个父母都会把他们的两个基因中的一个随机地传给他们的孩子,而且有一个 `PROBS["mutation"]` 的机会,即它会发生突变(从变异基因变成正常基因,或者相反)。
|
|
||||||
- 使用概率分布 `PROBS["trait"]` 来计算一个人具有或不具有形状的概率。
|
|
||||||
- `update` 函数将一个新的联合分布概率添加到 `probabilities` 中的现有概率分布中。
|
|
||||||
|
|
||||||
- 该函数接受五个值作为输入:`probabilities`, `one_gene`, `two_genes`, `have_trait`, 和 `p`。
|
- `people` 是一个在 "理解"一节中描述的人的字典。键代表名字,值是包含 `mother` 和 `father` 键的字典。你可以假设 `mother` 和 `father` 都是空白的(数据集中没有父母的信息),或者 `mother` 和 `father` 都会指代 `people` 字典中的其他人物。
|
||||||
|
- `one_gene` 是一个集合,我们想计算所有集合元素有一个变异基因的概率。
|
||||||
|
- `two_genes` 是一个集合,我们想计算所有集合元素有两个变异基因的概率。
|
||||||
|
- `have_trait` 是一个集合,我们想计算所有集合元素拥有该性状的概率。
|
||||||
|
- 对于不在 `one_gene` 或 t `wo_genes` 中的人,我们想计算他们没有变异基因的概率;对于不在 `have_trait` 中的人,我们想计算他们没有该性状的概率。
|
||||||
|
|
||||||
- `probabilities` 是一个在 "理解 "部分提到的字典。每个人都被映射到一个 `"gene"` 分布和一个 `"trait"` 分布。
|
- 例如,如果这个家庭由 Harry、James 和 Lily 组成,那么在 `one_gene = {"Harry"}`、`two_genes = {"James"}` 和 `trait = {"Harry"、"James"}` 的情况下调用这个函数,应该计算出 Lily 没有变异基因、Harry 拥有一个变异基因、James 拥有两个变异基因、Harry 表现出该性状、James 表现出该性状和 Lily 没有表现出该性状的联合概率。
|
||||||
- `one_gene` 是一个集合,我们想计算所有集合元素有一个变异基因的概率。
|
- 对于数据集中没有列出父母的人,使用概率分布 `PROBS["gene"]` 来确定他们有特定数量基因的概率。
|
||||||
- `two_genes` 是一个集合,我们想计算所有集合元素有两个变异基因的概率。
|
- 对于数据集中有父母的人来说,每个父母都会把他们的两个基因中的一个随机地传给他们的孩子,而且有一个 `PROBS["mutation"]` 的机会,即它会发生突变(从变异基因变成正常基因,或者相反)。
|
||||||
- `have_trait` 是一个集合,我们想计算所有集合元素拥有该性状的概率。
|
- 使用概率分布 `PROBS["trait"]` 来计算一个人具有或不具有形状的概率。
|
||||||
- `p` 是联合分布的概率。
|
|
||||||
- 对于概率中的每个人,该函数应该更新 `probabilities[person]["gene"]` 分布和 `probabilities[person]["trait"]` 分布,在每个分布中的适当数值上加上 `p`。所有其他数值应保持不变。
|
|
||||||
- 例如,如果"Harry"同时出现在 `two_genes` 和 `have_trait` 中,那么 `p` 将被添加到 `probabilities["Harry"]["gene"][2]` 和 `probabilities["Harry"]["trait"][True]`。
|
|
||||||
- 该函数不应返回任何值:它只需要更新 `probabilities` 字典。
|
|
||||||
- `normalize` 函数更新 `probabilities` 字典,使每个概率分布被归一化(即和为 1,相对比例相同)。
|
|
||||||
|
|
||||||
- 该函数接受一个单一的值:`probabilities`。
|
`update` 函数将一个新的联合分布概率添加到 `probabilities` 中的现有概率分布中。
|
||||||
|
|
||||||
- `probabilities` 是一个在"理解"部分提到的字典。每个人都被映射到一个 `"gene"` 分布和一个 `"trait"` 分布。
|
- 该函数接受五个值作为输入:`probabilities`, `one_gene`, `two_genes`, `have_trait`, 和 `p`。
|
||||||
- 对于 `probabilities` 中每个人的两个分布,这个函数应该将该分布归一化,使分布中的数值之和为 1,分布中的相对数值是相同的。
|
|
||||||
- 例如,如果 `probabilities["Harry"]["trait"][True]` 等于 `0.1`,概率 `probabilities["Harry"]["trait"][False]` 等于 `0.3`,那么你的函数应该将前一个值更新为 `0.25`,后一个值更新为 `0.75`: 现在数字之和为 1,而且后一个值仍然比前一个值大三倍。
|
- `probabilities` 是一个在 "理解 "部分提到的字典。每个人都被映射到一个 `"gene"` 分布和一个 `"trait"` 分布。
|
||||||
- 该函数不应返回任何值:它只需要更新 `probabilities` 字典。
|
- `one_gene` 是一个集合,我们想计算所有集合元素有一个变异基因的概率。
|
||||||
- 除了规范中要求你实现的三个函数外,你不应该修改 `heredity.py` 中的任何其他东西,尽管你可以编写额外的函数和/或导入其他 Python 标准库模块。如果熟悉的话,你也可以导入 `numpy` 或 `pandas`,但是你不应该使用任何其他第三方 Python 模块。
|
- `two_genes` 是一个集合,我们想计算所有集合元素有两个变异基因的概率。
|
||||||
|
- `have_trait` 是一个集合,我们想计算所有集合元素拥有该性状的概率。
|
||||||
|
- `p` 是联合分布的概率。
|
||||||
|
- 对于概率中的每个人,该函数应该更新 `probabilities[person]["gene"]` 分布和 `probabilities[person]["trait"]` 分布,在每个分布中的适当数值上加上 `p`。所有其他数值应保持不变。
|
||||||
|
- 例如,如果"Harry"同时出现在 `two_genes` 和 `have_trait` 中,那么 `p` 将被添加到 `probabilities["Harry"]["gene"][2]` 和 `probabilities["Harry"]["trait"][True]`。
|
||||||
|
- 该函数不应返回任何值:它只需要更新 `probabilities` 字典。
|
||||||
|
|
||||||
|
`normalize` 函数更新 `probabilities` 字典,使每个概率分布被归一化(即和为 1,相对比例相同)。
|
||||||
|
|
||||||
|
- 该函数接受一个单一的值:`probabilities`。
|
||||||
|
|
||||||
|
- `probabilities` 是一个在"理解"部分提到的字典。每个人都被映射到一个 `"gene"` 分布和一个 `"trait"` 分布。
|
||||||
|
- 对于 `probabilities` 中每个人的两个分布,这个函数应该将该分布归一化,使分布中的数值之和为 1,分布中的相对数值是相同的。
|
||||||
|
- 例如,如果 `probabilities["Harry"]["trait"][True]` 等于 `0.1`,概率 `probabilities["Harry"]["trait"][False]` 等于 `0.3`,那么你的函数应该将前一个值更新为 `0.25`,后一个值更新为 `0.75`: 现在数字之和为 1,而且后一个值仍然比前一个值大三倍。
|
||||||
|
- 该函数不应返回任何值:它只需要更新 `probabilities` 字典。
|
||||||
|
|
||||||
|
除了规范中要求你实现的三个函数外,你不应该修改 `heredity.py` 中的任何其他东西,尽管你可以编写额外的函数和/或导入其他 Python 标准库模块。如果熟悉的话,你也可以导入 `numpy` 或 `pandas`,但是你不应该使用任何其他第三方 Python 模块。
|
||||||
|
|
||||||
## 一个联合概率例子
|
## 一个联合概率例子
|
||||||
|
|
||||||
- 为了帮助你思考如何计算联合概率,我们在下面附上一个例子。
|
为了帮助你思考如何计算联合概率,我们在下面附上一个例子。
|
||||||
- 请考虑以下 `people` 的值:
|
|
||||||
|
请考虑以下 `people` 的值:
|
||||||
|
|
||||||
```python
|
```python
|
||||||
{
|
{
|
||||||
@@ -86,12 +102,17 @@
|
|||||||
}
|
}
|
||||||
```
|
```
|
||||||
|
|
||||||
- 这里我们将展示 `joint_probability(people, {"Harry"}, {"James"}, {"James"})` 的计算。根据参数,`one_gene` 是 `{"Harry"}`,`two_genes` 是 `{"James"}`,而 `has_trait` 是 `{"James"}`。因此,这代表了以下的概率:Lily 没有变异基因,不具有该性状;Harry 有一个变异基因,不具有该性状;James 有 2 个变异基因,具有该性状。
|
这里我们将展示 `joint_probability(people, {"Harry"}, {"James"}, {"James"})` 的计算。根据参数,`one_gene` 是 `{"Harry"}`,`two_genes` 是 `{"James"}`,而 `has_trait` 是 `{"James"}`。因此,这代表了以下的概率:Lily 没有变异基因,不具有该性状;Harry 有一个变异基因,不具有该性状;James 有 2 个变异基因,具有该性状。
|
||||||
- 我们从 Lily 开始(我们考虑人的顺序并不重要,只要我们把正确的数值乘在一起,因为乘法是可交换的)。Lily 没有变异基因,概率为 `0.96`(这就是 `PROBS["gene"][0]`)。鉴于她没有变异基因,她没有这个性状的概率为 `0.99`(这是 `PROBS["trait"][0][False]`)。因此,她没有变异基因且没有该性状的概率是 `0.96*0.99=0.9504`。
|
|
||||||
- 接下来,我们考虑 James。James 有 2 个变异基因,概率为 `0.01`(这是 `PROBS["gene"][2]`)。鉴于他有 2 个变异基因,他确实具有该性状的概率为 `0.65`。因此,他有 2 个变异基因并且他确实具有该性状的概率是 `0.01*0.65=0.0065`。
|
我们从 Lily 开始(我们考虑人的顺序并不重要,只要我们把正确的数值乘在一起,因为乘法是可交换的)。Lily 没有变异基因,概率为 `0.96`(这就是 `PROBS["gene"][0]`)。鉴于她没有变异基因,她没有这个性状的概率为 `0.99`(这是 `PROBS["trait"][0][False]`)。因此,她没有变异基因且没有该性状的概率是 `0.96*0.99=0.9504`。
|
||||||
- 最后,我们考虑 Harry。Harry 有 1 个变异基因的概率是多少?有两种情况可以发生。要么他从母亲那里得到这个基因,而不是从父亲那里,要么他从父亲那里得到这个基因,而不是从母亲那里。他的母亲 Lily 没有变异基因,所以 Harry 会以 `0.01` 的概率从他母亲那里得到这个基因(这是 `PROBS["mutation"]`),因为从他母亲那里得到这个基因的唯一途径是基因突变;相反,Harry 不会从他母亲那里得到这个基因,概率是 `0.99`。他的父亲 James 有 2 个变异基因,所以 Harry 会以 `0.99` 的概率从他父亲那里得到这个基因(这是 `1-PROBS["mutation"]`),但会以 `0.01` 的概率从他母亲那里得到这个基因(突变的概率)。这两种情况加在一起可以得到 `0.99*0.99+0.01*0.01=0.9802`,即 Harry 有 1 个变异基因的概率。
|
|
||||||
- 考虑到 Harry 有 1 个变异基因,他没有该性状的概率是 `0.44`(这是 `PROBS["trait"][1][false]`)。因此,哈利有 1 个变异基因而没有该性状的概率是 `0.9802 * 0.44 = 0.431288`。
|
接下来,我们考虑 James。James 有 2 个变异基因,概率为 `0.01`(这是 `PROBS["gene"][2]`)。鉴于他有 2 个变异基因,他确实具有该性状的概率为 `0.65`。因此,他有 2 个变异基因并且他确实具有该性状的概率是 `0.01*0.65=0.0065`。
|
||||||
- 因此,整个联合概率是三个人中每个人的所有这些数值相乘的结果:`0.9504 * 0.0065 * 0.431288 = 0.0026643247488`。
|
|
||||||
|
最后,我们考虑 Harry。Harry 有 1 个变异基因的概率是多少?有两种情况可以发生。要么他从母亲那里得到这个基因,而不是从父亲那里,要么他从父亲那里得到这个基因,而不是从母亲那里。他的母亲 Lily 没有变异基因,所以 Harry 会以 `0.01` 的概率从他母亲那里得到这个基因(这是 `PROBS["mutation"]`),因为从他母亲那里得到这个基因的唯一途径是基因突变;相反,Harry 不会从他母亲那里得到这个基因,概率是 `0.99`。他的父亲 James 有 2 个变异基因,所以 Harry 会以 `0.99` 的概率从他父亲那里得到这个基因(这是 `1-PROBS["mutation"]`),但会以 `0.01` 的概率从他母亲那里得到这个基因(突变的概率)。这两种情况加在一起可以得到 `0.99*0.99+0.01*0.01=0.9802`,即 Harry 有 1 个变异基因的概率。
|
||||||
|
|
||||||
|
考虑到 Harry 有 1 个变异基因,他没有该性状的概率是 `0.44`(这是 `PROBS["trait"][1][false]`)。因此,哈利有 1 个变异基因而没有该性状的概率是 `0.9802 * 0.44 = 0.431288`。
|
||||||
|
|
||||||
|
因此,整个联合概率是三个人中每个人的所有这些数值相乘的结果:`0.9504 * 0.0065 * 0.431288 = 0.0026643247488`。
|
||||||
|
|
||||||
## 提示
|
## 提示
|
||||||
|
|
||||||
|
|||||||
@@ -1,14 +1,14 @@
|
|||||||
# 不确定性问题
|
# 不确定性问题
|
||||||
|
|
||||||
- 上一讲中,我们讨论了人工智能如何表示和推导新知识。然而,在现实中,人工智能往往对世界只有部分了解,这给不确定性留下了空间。尽管如此,我们还是希望我们的人工智能在这些情况下做出尽可能好的决定。例如,在预测天气时,人工智能掌握了今天的天气信息,但无法 100% 准确地预测明天的天气。尽管如此,我们可以做得比偶然更好,今天的讲座是关于我们如何创造人工智能,在有限的信息和不确定性的情况下做出最佳决策。
|
上一讲中,我们讨论了人工智能如何表示和推导新知识。然而,在现实中,人工智能往往对世界只有部分了解,这给不确定性留下了空间。尽管如此,我们还是希望我们的人工智能在这些情况下做出尽可能好的决定。例如,在预测天气时,人工智能掌握了今天的天气信息,但无法 100% 准确地预测明天的天气。尽管如此,我们可以做得比偶然更好,今天的讲座是关于我们如何创造人工智能,在有限的信息和不确定性的情况下做出最佳决策。
|
||||||
|
|
||||||
## 概率 (Probability)
|
## 概率 (Probability)
|
||||||
|
|
||||||
- 不确定性可以表示为多个事件以及每一个事件发生的可能性或概率。
|
不确定性可以表示为多个事件以及每一个事件发生的可能性或概率。
|
||||||
|
|
||||||
### 概率世界
|
### 概率世界
|
||||||
|
|
||||||
- 每一种可能的情况都可以被视为一个世界,由小写的希腊字母$ω$表示。例如,掷骰子可以产生六个可能的世界:骰子出现 1 的世界,骰子出现 2 的世界,依此类推。为了表示某个世界的概率,我们写$P(ω)$。
|
每一种可能的情况都可以被视为一个世界,由小写的希腊字母$ω$表示。例如,掷骰子可以产生六个可能的世界:骰子出现 1 的世界,骰子出现 2 的世界,依此类推。为了表示某个世界的概率,我们写$P(ω)$。
|
||||||
|
|
||||||
### 概率公理
|
### 概率公理
|
||||||
|
|
||||||
@@ -18,45 +18,49 @@
|
|||||||
- 一般来说,值越高,事件发生的可能性就越大。
|
- 一般来说,值越高,事件发生的可能性就越大。
|
||||||
- 每一个可能发生的事件的概率加在一起等于 1。
|
- 每一个可能发生的事件的概率加在一起等于 1。
|
||||||
|
|
||||||
$\sum_{\omega\in\Omega}P(\omega)=1$
|
$$\sum_{\omega\in\Omega}P(\omega)=1$$
|
||||||
|
|
||||||
- 用标准骰子掷出数字 R 的概率可以表示为 $P(R)$ 。在我们的例子中,$P(R)=1/6$ ,因为有六个可能的世界(从 1 到 6 的任何数字),并且每个世界有相同的可能性发生。现在,考虑掷两个骰子的事件。现在,有 36 个可能的事件,同样有相同的可能性发生。
|
用标准骰子掷出数字 R 的概率可以表示为 $P(R)$ 。在我们的例子中,$P(R)=1/6$ ,因为有六个可能的世界(从 1 到 6 的任何数字),并且每个世界有相同的可能性发生。现在,考虑掷两个骰子的事件。现在,有 36 个可能的事件,同样有相同的可能性发生。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 然而,如果我们试图预测两个骰子的总和,会发生什么?在这种情况下,我们只有 11 个可能的值(总和必须在 2 到 12 之间),而且它们的出现频率并不相同。
|
然而,如果我们试图预测两个骰子的总和,会发生什么?在这种情况下,我们只有 11 个可能的值(总和必须在 2 到 12 之间),而且它们的出现频率并不相同。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 为了得到事件发生的概率,我们将事件发生的世界数量除以可能发生的世界总数。例如,当掷两个骰子时,有 36 个可能的世界。只有在其中一个世界中,当两个骰子都得到 6 时,我们才能得到 12 的总和。因此,$P(12)=\frac{1}{36}$,或者,换句话说,掷两个骰子并得到两个和为 12 的数字的概率是$\frac{1}{36}$。$P(7)$是多少?我们数了数,发现和 7 出现在 6 个世界中。因此,$P(7)=\frac{6}{36}=\frac{1}{6}$。
|
为了得到事件发生的概率,我们将事件发生的世界数量除以可能发生的世界总数。例如,当掷两个骰子时,有 36 个可能的世界。只有在其中一个世界中,当两个骰子都得到 6 时,我们才能得到 12 的总和。因此,$P(12)=\frac{1}{36}$,或者,换句话说,掷两个骰子并得到两个和为 12 的数字的概率是$\frac{1}{36}$。$P(7)$是多少?我们数了数,发现和 7 出现在 6 个世界中。因此,$P(7)=\frac{6}{36}=\frac{1}{6}$。
|
||||||
|
|
||||||
### 无条件概率 (Unconditional Probability)
|
### 无条件概率 (Unconditional Probability)
|
||||||
|
|
||||||
- 无条件概率是指在没有任何其他证据的情况下对命题发生的概率。到目前为止,我们所问的所有问题都是无条件概率的问题,因为掷骰子的结果并不取决于之前的事件。
|
无条件概率是指在没有任何其他证据的情况下对命题发生的概率。到目前为止,我们所问的所有问题都是无条件概率的问题,因为掷骰子的结果并不取决于之前的事件。
|
||||||
|
|
||||||
## 条件概率 (Conditional Probability)
|
## 条件概率 (Conditional Probability)
|
||||||
|
|
||||||
- 条件概率是在给定一些已经揭示的证据的情况下,命题发生的概率。正如引言中所讨论的,人工智能可以利用部分信息对未来进行有根据的猜测。为了使用这些影响事件在未来发生概率的信息,我们需要依赖条件概率。
|
条件概率是在给定一些已经揭示的证据的情况下,命题发生的概率。正如引言中所讨论的,人工智能可以利用部分信息对未来进行有根据的猜测。为了使用这些影响事件在未来发生概率的信息,我们需要依赖条件概率。
|
||||||
- 条件概率用以下符号表示:$P(a|b)$,意思是“如果我们知道事件$b$已经发生,事件$a$发生的概率”,或者更简洁地说,“给定$b$的概率”。现在我们可以问一些问题,比如如果昨天下雨,今天下雨的概率是多少$P(今天下雨 | 昨天下雨)$,或者给定患者的测试结果,患者患有该疾病的概率 $P(疾病 | 测试结果)$ 是多少。
|
|
||||||
- 在数学上,为了计算给定$b$的条件概率,我们使用公式:$P(a|b)=\frac{P(a\land b)}{P(b)}$
|
条件概率用以下符号表示:$P(a|b)$,意思是“如果我们知道事件$b$已经发生,事件$a$发生的概率”,或者更简洁地说,“给定$b$的概率”。现在我们可以问一些问题,比如如果昨天下雨,今天下雨的概率是多少$P(今天下雨 | 昨天下雨)$,或者给定患者的测试结果,患者患有该疾病的概率 $P(疾病 | 测试结果)$ 是多少。
|
||||||
- 换句话说,给定$b$为真的概率等于$a$并且$b$为真,除以$b$的概率。对此进行推理的一种直观方式是认为“我们对$a$并且$b$都为真的事件(分子)感兴趣,但只对我们知道$b$为真(分母)的世界感兴趣。“除以 $b$ 将可能的世界限制在 $b$ 为真的世界。以下是上述公式的代数等价形式:
|
|
||||||
|
在数学上,为了计算给定$b$的条件概率,我们使用公式:$P(a|b)=\frac{P(a\land b)}{P(b)}$
|
||||||
|
|
||||||
|
换句话说,给定$b$为真的概率等于$a$并且$b$为真,除以$b$的概率。对此进行推理的一种直观方式是认为“我们对$a$并且$b$都为真的事件(分子)感兴趣,但只对我们知道$b$为真(分母)的世界感兴趣。“除以 $b$ 将可能的世界限制在 $b$ 为真的世界。以下是上述公式的代数等价形式:
|
||||||
|
|
||||||
$P(a\land b)=P(b)P(a|b)$
|
$P(a\land b)=P(b)P(a|b)$
|
||||||
|
|
||||||
$P(a\land b)=P(a)P(b|a)$
|
$P(a\land b)=P(a)P(b|a)$
|
||||||
|
|
||||||
- 例如,考虑$P(总和为 12|在一个骰子上掷出 6)$,或者掷两个骰子假设我们已经掷了一个骰子并获得了六,得到十二的概率。为了计算这一点,我们首先将我们的世界限制在第一个骰子的值为六的世界:
|
例如,考虑$P(总和为 12|在一个骰子上掷出 6)$,或者掷两个骰子假设我们已经掷了一个骰子并获得了六,得到十二的概率。为了计算这一点,我们首先将我们的世界限制在第一个骰子的值为六的世界:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 现在我们问,在我们将问题限制在(除以$P(6)$,或第一个骰子产生 6 的概率)的世界中,事件 a(和为 12)发生了多少次?
|
现在我们问,在我们将问题限制在(除以$P(6)$,或第一个骰子产生 6 的概率)的世界中,事件 a(和为 12)发生了多少次?
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
## 随机变量 (Random Variables)
|
## 随机变量 (Random Variables)
|
||||||
|
|
||||||
- 随机变量是概率论中的一个变量,它有一个可能取值的域。例如,为了表示掷骰子时的可能结果,我们可以定义一个随机变量 Roll,它可以取值$\set{0,1,2,3,4,5,6}$。为了表示航班的状态,我们可以定义一个变量 flight,它采用$\set{准时、延迟、取消}$的值。
|
随机变量是概率论中的一个变量,它有一个可能取值的域。例如,为了表示掷骰子时的可能结果,我们可以定义一个随机变量 Roll,它可以取值$\set{0,1,2,3,4,5,6}$。为了表示航班的状态,我们可以定义一个变量 flight,它采用$\set{准时、延迟、取消}$的值。
|
||||||
- 通常,我们对每个值发生的概率感兴趣。我们用概率分布来表示这一点。例如:
|
|
||||||
|
通常,我们对每个值发生的概率感兴趣。我们用概率分布来表示这一点。例如:
|
||||||
|
|
||||||
$P(Flight=准时)=0.6$
|
$P(Flight=准时)=0.6$
|
||||||
|
|
||||||
@@ -64,30 +68,37 @@ $P(Flight=延迟)=0.3$
|
|||||||
|
|
||||||
$P(Flight=取消)=0.1$
|
$P(Flight=取消)=0.1$
|
||||||
|
|
||||||
- 用文字来解释概率分布,这意味着航班准时的可能性为 60%,延误的可能性为 30%,取消的可能性为 10%。注意,如前所述,所有可能结果的概率之和为 1。
|
用文字来解释概率分布,这意味着航班准时的可能性为 60%,延误的可能性为 30%,取消的可能性为 10%。注意,如前所述,所有可能结果的概率之和为 1。
|
||||||
- 概率分布可以更简洁地表示为向量。例如,$P(Flight)=<0.6,0.3,0.1>$。为了便于解释,这些值有一个固定的顺序(在我们的情况下,准时、延迟、取消)。
|
|
||||||
|
概率分布可以更简洁地表示为向量。例如,$P(Flight)=<0.6,0.3,0.1>$。为了便于解释,这些值有一个固定的顺序(在我们的情况下,准时、延迟、取消)。
|
||||||
|
|
||||||
### 独立性 (Independence)
|
### 独立性 (Independence)
|
||||||
|
|
||||||
- 独立性是指一个事件的发生不会影响另一个事件发生的概率。例如,当掷两个骰子时,每个骰子的结果与另一个骰子的结果是独立的。用第一个骰子掷出 4 不会影响我们掷出的第二个骰子的值。这与依赖事件相反,比如早上的云和下午的雨。如果早上多云,下午更有可能下雨,所以这些事件是有依赖性的。
|
独立性是指一个事件的发生不会影响另一个事件发生的概率。例如,当掷两个骰子时,每个骰子的结果与另一个骰子的结果是独立的。用第一个骰子掷出 4 不会影响我们掷出的第二个骰子的值。这与依赖事件相反,比如早上的云和下午的雨。如果早上多云,下午更有可能下雨,所以这些事件是有依赖性的。
|
||||||
- 独立性可以用数学定义:事件$a$和$b$是独立的,当且仅当$a$并且$b$的概率等于$a$的概率乘以$b$的概率:$P(a∧b)=P(a)P(b)$。
|
|
||||||
|
独立性可以用数学定义:事件$a$和$b$是独立的,当且仅当$a$并且$b$的概率等于$a$的概率乘以$b$的概率:$P(a∧b)=P(a)P(b)$。
|
||||||
|
|
||||||
## 贝叶斯规则 (Bayes’Rule)
|
## 贝叶斯规则 (Bayes’Rule)
|
||||||
|
|
||||||
- 贝叶斯规则在概率论中常用来计算条件概率。换句话说,贝叶斯规则说,给定$b$条件下$a$的概率等于给定$a$的条件下$b$概率,乘以$b$的概率除以$a$ 的概率。
|
贝叶斯规则在概率论中常用来计算条件概率。换句话说,贝叶斯规则说,给定$b$条件下$a$的概率等于给定$a$的条件下$b$概率,乘以$b$的概率除以$a$ 的概率。
|
||||||
- $P(b|a)=\frac{P(a|b)P(b)}{P(a)}$
|
|
||||||
- 例如,如果早上有云,我们想计算下午下雨的概率,或者$P(雨 | 云)$。我们从以下信息开始:
|
|
||||||
|
|
||||||
- 80% 的雨天下午开始于多云的早晨,或$P(云 | 雨)$。
|
$P(b|a)=\frac{P(a|b)P(b)}{P(a)}$
|
||||||
- 40% 的日子早晨多云,或$P(云)$。
|
|
||||||
- 10% 的日子有下雨的下午,或$P(雨)$。
|
例如,如果早上有云,我们想计算下午下雨的概率,或者$P(雨 | 云)$。我们从以下信息开始:
|
||||||
- 应用贝叶斯规则,我们计算$\frac{0.8*0.1}{0.4}=0.2$。也就是说,考虑到早上多云,下午下雨的可能性是 20%。
|
|
||||||
- 除了$P(a)$和$P(b)$之外,知道$P(a|b)$还允许我们计算$P(b|a)$。这是有帮助的,因为知道给定未知原因的可见效应的条件概率$P(可见效应 | 未知原因)$,可以让我们计算给定可见效应的未知原因的概率$P(未知原因 | 可见效应)$。例如,我们可以通过医学试验来学习$P(医学测试结果 | 疾病)$,在医学试验中,我们对患有该疾病的人进行测试,并观察测试结果发生的频率。知道了这一点,我们就可以计算出$P(疾病 | 医学检测结果)$,这是有价值的诊断信息。
|
- 80% 的雨天下午开始于多云的早晨,或$P(云 | 雨)$。
|
||||||
|
- 40% 的日子早晨多云,或$P(云)$。
|
||||||
|
- 10% 的日子有下雨的下午,或$P(雨)$。
|
||||||
|
|
||||||
|
应用贝叶斯规则,我们计算$\frac{0.8*0.1}{0.4}=0.2$。也就是说,考虑到早上多云,下午下雨的可能性是 20%。
|
||||||
|
|
||||||
|
除了$P(a)$和$P(b)$之外,知道$P(a|b)$还允许我们计算$P(b|a)$。这是有帮助的,因为知道给定未知原因的可见效应的条件概率$P(可见效应 | 未知原因)$,可以让我们计算给定可见效应的未知原因的概率$P(未知原因 | 可见效应)$。例如,我们可以通过医学试验来学习$P(医学测试结果 | 疾病)$,在医学试验中,我们对患有该疾病的人进行测试,并观察测试结果发生的频率。知道了这一点,我们就可以计算出$P(疾病 | 医学检测结果)$,这是有价值的诊断信息。
|
||||||
|
|
||||||
## 联合概率 (Joint Probability)
|
## 联合概率 (Joint Probability)
|
||||||
|
|
||||||
- 联合概率是指多个事件全部发生的可能性。
|
联合概率是指多个事件全部发生的可能性。
|
||||||
- 让我们考虑下面的例子,关于早上有云,下午有雨的概率。
|
|
||||||
|
让我们考虑下面的例子,关于早上有云,下午有雨的概率。
|
||||||
|
|
||||||
| C=云 | C=$\lnot$云 |
|
| C=云 | C=$\lnot$云 |
|
||||||
| ---- | ----------- |
|
| ---- | ----------- |
|
||||||
@@ -97,95 +108,105 @@ $P(Flight=取消)=0.1$
|
|||||||
| ---- | ----------- |
|
| ---- | ----------- |
|
||||||
| 0.1 | 0.9 |
|
| 0.1 | 0.9 |
|
||||||
|
|
||||||
- 从这些数据来看,我们无法判断早上的云是否与下午下雨的可能性有关。为了做到这一点,我们需要看看这两个变量所有可能结果的联合概率。我们可以将其表示在下表中:
|
从这些数据来看,我们无法判断早上的云是否与下午下雨的可能性有关。为了做到这一点,我们需要看看这两个变量所有可能结果的联合概率。我们可以将其表示在下表中:
|
||||||
|
|
||||||
| | R=雨 | R=$\lnot$ 雨 |
|
| | R=雨 | R=$\lnot$ 雨 |
|
||||||
| ----------- | ---- | ------------ |
|
| ----------- | ---- | ------------ |
|
||||||
| C=云 | 0.08 | 0.32 |
|
| C=云 | 0.08 | 0.32 |
|
||||||
| C=$\lnot$云 | 0.02 | 0.58 |
|
| C=$\lnot$云 | 0.02 | 0.58 |
|
||||||
|
|
||||||
- 现在我们可以知道有关这些事件同时发生的信息了。例如,我们知道某一天早上有云,下午有雨的概率是 0.08。早上没有云,下午没有雨的概率是 0.58。
|
现在我们可以知道有关这些事件同时发生的信息了。例如,我们知道某一天早上有云,下午有雨的概率是 0.08。早上没有云,下午没有雨的概率是 0.58。
|
||||||
- 使用联合概率,我们可以推导出条件概率。例如,如果我们感兴趣的是在下午下雨的情况下,早上云层的概率分布。$P(C|雨)=\frac{P(C,雨)}{P(雨)}$旁注:在概率上,逗号和$∧$可以互换使用。因此,$P(C,雨)=P(C\land 雨)$。换句话说,我们将降雨和云层的联合概率除以降雨的概率。
|
|
||||||
- 在最后一个方程中,可以将$P(雨)$视为$P(C,雨)$乘以的某个常数$\alpha=\frac{1}{P(雨)}$。因此,我们可以重写$P(C|雨)=\frac{P(C,雨)}{P(雨)}=αP(C,雨)$,或$α<0.08,0.02>=<0.8,0.2>$。考虑到下午有雨,将$α$分解后,我们可以得到 C 的可能值的概率比例。也就是说,如果下午有雨,那么早上有云和早上没有云的概率的比例是$0.08:0.02$。请注意,0.08 和 0.02 的总和不等于 1;然而,由于这是随机变量 C 的概率分布,我们知道它们应该加起来为 1。因此,我们需要通过算$α$来归一化这些值,使得$α0.08+α0.02=1$。最后,我们可以说$P(C|雨)=<0.8,0.2>$。
|
使用联合概率,我们可以推导出条件概率。例如,如果我们感兴趣的是在下午下雨的情况下,早上云层的概率分布。$P(C|雨)=\frac{P(C,雨)}{P(雨)}$旁注:在概率上,逗号和$∧$可以互换使用。因此,$P(C,雨)=P(C\land 雨)$。换句话说,我们将降雨和云层的联合概率除以降雨的概率。
|
||||||
|
|
||||||
|
在最后一个方程中,可以将$P(雨)$视为$P(C,雨)$乘以的某个常数$\alpha=\frac{1}{P(雨)}$。因此,我们可以重写$P(C|雨)=\frac{P(C,雨)}{P(雨)}=αP(C,雨)$,或$α<0.08,0.02>=<0.8,0.2>$。考虑到下午有雨,将$α$分解后,我们可以得到 C 的可能值的概率比例。也就是说,如果下午有雨,那么早上有云和早上没有云的概率的比例是$0.08:0.02$。请注意,0.08 和 0.02 的总和不等于 1;然而,由于这是随机变量 C 的概率分布,我们知道它们应该加起来为 1。因此,我们需要通过算$α$来归一化这些值,使得$α0.08+α0.02=1$。最后,我们可以说$P(C|雨)=<0.8,0.2>$。
|
||||||
|
|
||||||
## 概率规则 (Probability Rules)
|
## 概率规则 (Probability Rules)
|
||||||
|
|
||||||
- 否定 (Negation): $P(\lnot a)=1-P(a)$。这源于这样一个事实,即所有可能世界的概率之和为 1,互补事件$\lnot a$和 $a$ 包括所有可能世界。
|
- 否定 (Negation): $P(\lnot a)=1-P(a)$。这源于这样一个事实,即所有可能世界的概率之和为 1,互补事件$\lnot a$和 $a$ 包括所有可能世界。
|
||||||
- 包含 - 排除 Inclusion-Exclusion:$P(a\lor b)=P(a)+P(b)-P(a\land b)$。这可以用以下方式解释:$a$或$b$为真的世界等于$a$为真的所有世界,加上$b$为真的所有世界。然而,在这种情况下,有些世界被计算两次(a 和$b$都为真的世界)。为了消除这种重叠,我们将$a$和$b$ 都为真的世界减去一次(因为它们被计算了两次)。
|
- 包含 - 排除 Inclusion-Exclusion:$P(a\lor b)=P(a)+P(b)-P(a\land b)$。这可以用以下方式解释:$a$或$b$为真的世界等于$a$为真的所有世界,加上$b$为真的所有世界。然而,在这种情况下,有些世界被计算两次(a 和$b$都为真的世界)。为了消除这种重叠,我们将$a$和$b$ 都为真的世界减去一次(因为它们被计算了两次)。
|
||||||
|
|
||||||
> 下面是一个例子,可以说明这一点。假设我 80% 的时间吃冰淇淋,70% 的时间吃饼干。如果我们计算今天我吃冰淇淋或饼干的概率,不减去$P(冰淇淋∧饼干)$,我们错误地得出 0.7+0.8=1.5。这与概率在 0 和 1 之间的公理相矛盾。为了纠正我同时吃冰淇淋和饼干的天数计算两次的错误,我们需要减去$P(冰淇淋∧饼干)$一次。
|
> 下面是一个例子,可以说明这一点。假设我 80% 的时间吃冰淇淋,70% 的时间吃饼干。如果我们计算今天我吃冰淇淋或饼干的概率,不减去$P(冰淇淋∧饼干)$,我们错误地得出 0.7+0.8=1.5。这与概率在 0 和 1 之间的公理相矛盾。为了纠正我同时吃冰淇淋和饼干的天数计算两次的错误,我们需要减去$P(冰淇淋∧饼干)$一次。
|
||||||
|
|
||||||
- 边缘化 (Marginalization):$P(a)=P(a,b)+P(a,\lnot b)$。这里的观点是,$b$和$\lnot b$是独立的概率。也就是说,$b$和$\lnot b$同时发生的概率为 0。我们也知道$b$和$\lnot b$的总和为 1。因此,当$a$发生时,$b$可以发生也可以不发生。当我们把$a$和$b$发生的概率加上$a$和$\lnot b$的概率时,我们得到的只是$a$ 的概率。
|
- 边缘化 (Marginalization):$P(a)=P(a,b)+P(a,\lnot b)$。这里的观点是,$b$和$\lnot b$是独立的概率。也就是说,$b$和$\lnot b$同时发生的概率为 0。我们也知道$b$和$\lnot b$的总和为 1。因此,当$a$发生时,$b$可以发生也可以不发生。当我们把$a$和$b$发生的概率加上$a$和$\lnot b$的概率时,我们得到的只是$a$ 的概率。
|
||||||
- 随机变量的边缘化可以用:$P(X=x_i)=\sum_jP(X=x_i,Y=y_j)$表示
|
|
||||||
- 方程的左侧表示“随机变量$X$具有$x_i$值的概率”例如,对于我们前面提到的变量 C,两个可能的值是早上有云和早上没有云。等式的正确部分是边缘化的概念。$P(X=x_i)$等于$x_i$以及随机变量$Y$的每一个值的所有联合概率之和。例如,$P(C=云)=P(C=云,R=雨)+P(C=云,R=\lnot 雨)=0.08+0.32=0.4$。
|
|
||||||
|
|
||||||
- 条件边缘化:$P(a)=P(a|b)P(b)+P(a|\lnot b)P(\lnot b)$。这是一个类似于边缘化的想法。事件$a$发生的概率等于给定$b$的概率乘以$b$的概率,再加上给定$\lnot b$的概率乘以$\lnot b$ 的概率。
|
随机变量的边缘化可以用:$P(X=x_i)=\sum_jP(X=x_i,Y=y_j)$表示
|
||||||
- $P(X=x_i)=\sum_jP(X=x_i|Y=y_i)P(Y=y_i)$
|
|
||||||
- 在这个公式中,随机变量$X$取$x_i$值概率等于$x_i$以及随机变量$Y$的每个值的联合概率乘以变量$Y$取该值的概率之和。如果我们还记得$P(a|b)=\frac{P(a,b)}{P(b)}$,就可以理解这个公式。如果我们将这个表达式乘以$P(b)$,我们得到$P(a,b)$,从这里开始,我们做的与边缘化相同。
|
方程的左侧表示“随机变量$X$具有$x_i$值的概率”例如,对于我们前面提到的变量 C,两个可能的值是早上有云和早上没有云。等式的正确部分是边缘化的概念。$P(X=x_i)$等于$x_i$以及随机变量$Y$的每一个值的所有联合概率之和。例如,$P(C=云)=P(C=云,R=雨)+P(C=云,R=\lnot 雨)=0.08+0.32=0.4$。
|
||||||
|
|
||||||
|
- 条件边缘化:$P(a)=P(a|b)P(b)+P(a|\lnot b)P(\lnot b)$。这是一个类似于边缘化的想法。事件$a$发生的概率等于给定$b$的概率乘以$b$的概率,再加上给定$\lnot b$的概率乘以$\lnot b$ 的概率。
|
||||||
|
|
||||||
|
$P(X=x_i)=\sum_jP(X=x_i|Y=y_i)P(Y=y_i)$
|
||||||
|
|
||||||
|
在这个公式中,随机变量$X$取$x_i$值概率等于$x_i$以及随机变量$Y$的每个值的联合概率乘以变量$Y$取该值的概率之和。如果我们还记得$P(a|b)=\frac{P(a,b)}{P(b)}$,就可以理解这个公式。如果我们将这个表达式乘以$P(b)$,我们得到$P(a,b)$,从这里开始,我们做的与边缘化相同。
|
||||||
|
|
||||||
## 贝叶斯网络 (Bayesian Networks)
|
## 贝叶斯网络 (Bayesian Networks)
|
||||||
|
|
||||||
- 贝叶斯网络是一种表示随机变量之间相关性的数据结构。贝叶斯网络具有以下属性:
|
贝叶斯网络是一种表示随机变量之间相关性的数据结构。贝叶斯网络具有以下属性:
|
||||||
|
|
||||||
- 它们是有向图。
|
- 它们是有向图。
|
||||||
- 图上的每个节点表示一个随机变量。
|
- 图上的每个节点表示一个随机变量。
|
||||||
- 从 X 到 Y 的箭头表示 X 是 Y 的父对象。也就是说,Y 的概率分布取决于 X 的值。
|
- 从 X 到 Y 的箭头表示 X 是 Y 的父对象。也就是说,Y 的概率分布取决于 X 的值。
|
||||||
- 每个节点 X 具有概率分布$P(X|Parents(X))$。
|
- 每个节点 X 具有概率分布$P(X|Parents(X))$。
|
||||||
- 让我们考虑一个贝叶斯网络的例子,该网络包含影响我们是否按时赴约的随机变量。
|
|
||||||
|
让我们考虑一个贝叶斯网络的例子,该网络包含影响我们是否按时赴约的随机变量。
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
- 让我们从上到下描述这个贝叶斯网络:
|
让我们从上到下描述这个贝叶斯网络:
|
||||||
|
|
||||||
- rain 是这个网络的根节点。这意味着它的概率分布不依赖于任何先前的事件。在我们的例子中,Rain 是一个随机变量,可以采用以下概率分布的值$\set{none,light,heavy}$:
|
- rain 是这个网络的根节点。这意味着它的概率分布不依赖于任何先前的事件。在我们的例子中,Rain 是一个随机变量,可以采用以下概率分布的值$\set{none,light,heavy}$:
|
||||||
|
|
||||||
| none | light | heavy |
|
| none | light | heavy |
|
||||||
| ---- | ----- | ----- |
|
| ---- | ----- | ----- |
|
||||||
| 0.7 | 0.2 | 0.1 |
|
| 0.7 | 0.2 | 0.1 |
|
||||||
|
|
||||||
- Maintenance 对是否有列车轨道维护进行编码,取值为$\set{yes,no}$。Rain 是 Maintenance 的父节点,这意味着 Maintenance 概率分布受到 Rain 的影响。
|
- Maintenance 对是否有列车轨道维护进行编码,取值为$\set{yes,no}$。Rain 是 Maintenance 的父节点,这意味着 Maintenance 概率分布受到 Rain 的影响。
|
||||||
|
|
||||||
| R | yes | no |
|
| R | yes | no |
|
||||||
| ----- | --- | --- |
|
| ----- | --- | --- |
|
||||||
| none | 0.4 | 0.6 |
|
| none | 0.4 | 0.6 |
|
||||||
| light | 0.2 | 0.8 |
|
| light | 0.2 | 0.8 |
|
||||||
| heavy | 0.1 | 0.9 |
|
| heavy | 0.1 | 0.9 |
|
||||||
|
|
||||||
- Train 是一个变量,用于编码列车是准时还是晚点,取值为$\set{on\ time,delayed}$。请注意,列车上被“Maintenance”和“rain”指向。这意味着两者都是 Train 的父对象,它们的值会影响 Train 的概率分布。
|
- Train 是一个变量,用于编码列车是准时还是晚点,取值为$\set{on\ time,delayed}$。请注意,列车上被“Maintenance”和“rain”指向。这意味着两者都是 Train 的父对象,它们的值会影响 Train 的概率分布。
|
||||||
|
|
||||||
| R | M | On time | Delayed |
|
| R | M | On time | Delayed |
|
||||||
| ------ | --- | ------- | ------- |
|
| ------ | --- | ------- | ------- |
|
||||||
| none | yes | 0.8 | 0.2 |
|
| none | yes | 0.8 | 0.2 |
|
||||||
| none | no | 0.9 | 0.1 |
|
| none | no | 0.9 | 0.1 |
|
||||||
| light | yes | 0.6 | 0.4 |
|
| light | yes | 0.6 | 0.4 |
|
||||||
| light | no | 0.7 | 0.3 |
|
| light | no | 0.7 | 0.3 |
|
||||||
| heavry | yes | 0.4 | 0.6 |
|
| heavry | yes | 0.4 | 0.6 |
|
||||||
| heavy | no | 0.5 | 0.5 |
|
| heavy | no | 0.5 | 0.5 |
|
||||||
|
|
||||||
- Appointment 是一个随机变量,表示我们是否参加约会,取值为$\set{attend, miss}$。请注意,它唯一的父级是 Train。关于贝叶斯网络的这一点值得注意:父子只包括直接关系。的确,Maintenance 会影响 Train 是否准时,而 Train 是否准时会影响我们是否赴约。然而,最终,直接影响我们赴约机会的是 Train 是否准时,这就是贝叶斯网络所代表的。例如,如果火车准时到达,可能会有大雨和轨道维护,但这对我们是否赴约没有影响。
|
- Appointment 是一个随机变量,表示我们是否参加约会,取值为$\set{attend, miss}$。请注意,它唯一的父级是 Train。关于贝叶斯网络的这一点值得注意:父子只包括直接关系。的确,Maintenance 会影响 Train 是否准时,而 Train 是否准时会影响我们是否赴约。然而,最终,直接影响我们赴约机会的是 Train 是否准时,这就是贝叶斯网络所代表的。例如,如果火车准时到达,可能会有大雨和轨道维护,但这对我们是否赴约没有影响。
|
||||||
|
|
||||||
| T | attend | miss |
|
| T | attend | miss |
|
||||||
| ------- | ------ | ---- |
|
| ------- | ------ | ---- |
|
||||||
| on time | 0.9 | 0.1 |
|
| on time | 0.9 | 0.1 |
|
||||||
| delayed | 0.6 | 0.4 |
|
| delayed | 0.6 | 0.4 |
|
||||||
|
|
||||||
- 例如,如果我们想找出在没有维护和小雨的一天火车晚点时错过约会的概率,或者$P(light,no,delayed,miss)$,我们将计算如下:$P(light)P(no|light)P(delayed|light,no)P(miss|delayed)$。每个单独概率的值可以在上面的概率分布中找到,然后将这些值相乘以产生$P(light,no,delayed,miss)$。
|
例如,如果我们想找出在没有维护和小雨的一天火车晚点时错过约会的概率,或者$P(light,no,delayed,miss)$,我们将计算如下:$P(light)P(no|light)P(delayed|light,no)P(miss|delayed)$。每个单独概率的值可以在上面的概率分布中找到,然后将这些值相乘以产生$P(light,no,delayed,miss)$。
|
||||||
|
|
||||||
### 推理 (Inference)
|
### 推理 (Inference)
|
||||||
|
|
||||||
- 在知识推理,我们通过蕴含来看待推理。这意味着我们可以在现有信息的基础上得出新的信息。我们也可以根据概率推断出新的信息。虽然这不能让我们确切地知道新的信息,但它可以让我们计算出一些值的概率分布。推理具有多个属性。
|
在知识推理,我们通过蕴含来看待推理。这意味着我们可以在现有信息的基础上得出新的信息。我们也可以根据概率推断出新的信息。虽然这不能让我们确切地知道新的信息,但它可以让我们计算出一些值的概率分布。推理具有多个属性。
|
||||||
- Query 查询变量 $X$:我们要计算概率分布的变量。
|
- Query 查询变量 $X$:我们要计算概率分布的变量。
|
||||||
- Evidence variables 证据变量$E$: 一个或多个观测到事件$e$ 的变量。例如,我们可能观测到有小雨,这一观测有助于我们计算火车延误的概率。
|
- Evidence variables 证据变量$E$: 一个或多个观测到事件$e$ 的变量。例如,我们可能观测到有小雨,这一观测有助于我们计算火车延误的概率。
|
||||||
- Hidden variables 隐藏变量 $H$: 不是查询结论的变量,也没有被观测到。例如,站在火车站,我们可以观察是否下雨,但我们不知道道路后面的轨道是否有维修。因此,在这种情况下,Maintenance 将是一个隐藏的变量。
|
- Hidden variables 隐藏变量 $H$: 不是查询结论的变量,也没有被观测到。例如,站在火车站,我们可以观察是否下雨,但我们不知道道路后面的轨道是否有维修。因此,在这种情况下,Maintenance 将是一个隐藏的变量。
|
||||||
- The goal 目标:计算$P(X|e)$。例如,根据我们知道有小雨的证据 $e$ 计算 Train 变量 (查询) 的概率分布。
|
- The goal 目标:计算$P(X|e)$。例如,根据我们知道有小雨的证据 $e$ 计算 Train 变量 (查询) 的概率分布。
|
||||||
- 举一个例子。考虑到有小雨和没有轨道维护的证据,我们想计算 Appointment 变量的概率分布。也就是说,我们知道有小雨,没有轨道维护,我们想弄清楚我们参加约会和错过约会的概率是多少,$P(Appointment|light,no)$。从联合概率部分中,我们知道我们可以将约会随机变量的可能值表示为一个比例,将$P(Appointment|light,no)$重写为$αP(Appointment,light,no)$。如果 Appointment 的父节点仅为 Train 变量,而不是 Rain 或 Maintenance,我们如何计算约会的概率分布?在这里,我们将使用边缘化。$P(Appointment,light,no)$的值等于$α[P(Appointment,light,no,delay)+P(Appointment,light,no,on\ time)]$。
|
|
||||||
|
举一个例子。考虑到有小雨和没有轨道维护的证据,我们想计算 Appointment 变量的概率分布。也就是说,我们知道有小雨,没有轨道维护,我们想弄清楚我们参加约会和错过约会的概率是多少,$P(Appointment|light,no)$。从联合概率部分中,我们知道我们可以将约会随机变量的可能值表示为一个比例,将$P(Appointment|light,no)$重写为$αP(Appointment,light,no)$。如果 Appointment 的父节点仅为 Train 变量,而不是 Rain 或 Maintenance,我们如何计算约会的概率分布?在这里,我们将使用边缘化。$P(Appointment,light,no)$的值等于$α[P(Appointment,light,no,delay)+P(Appointment,light,no,on\ time)]$。
|
||||||
|
|
||||||
### 枚举推理
|
### 枚举推理
|
||||||
|
|
||||||
- 枚举推理是在给定观测证据$e$和一些隐藏变量$Y$的情况下,找到变量$X$ 的概率分布的过程。
|
枚举推理是在给定观测证据$e$和一些隐藏变量$Y$的情况下,找到变量$X$ 的概率分布的过程。
|
||||||
- $P(X|e)=\alpha P(X,e)=\alpha \sum_yP(X,e,y)$
|
|
||||||
- 在这个方程中,$X$代表查询变量,$e$代表观察到的证据,$y$代表隐藏变量的所有值,$α$归一化结果,使我们最终得到的概率加起来为 1。用文字来解释这个方程,即给定$e$的$X$的概率分布等于$X$和$e$的归一化概率分布。为了得到这个分布,我们对$X、e$和$y$的归一化概率求和,其中$y$每次取隐藏变量$Y$ 的不同值。
|
$P(X|e)=\alpha P(X,e)=\alpha \sum_yP(X,e,y)$
|
||||||
- Python 中存在多个库,以简化概率推理过程。我们将查看库 `pomegranate`,看看如何在代码中表示上述数据。
|
|
||||||
|
在这个方程中,$X$代表查询变量,$e$代表观察到的证据,$y$代表隐藏变量的所有值,$α$归一化结果,使我们最终得到的概率加起来为 1。用文字来解释这个方程,即给定$e$的$X$的概率分布等于$X$和$e$的归一化概率分布。为了得到这个分布,我们对$X、e$和$y$的归一化概率求和,其中$y$每次取隐藏变量$Y$ 的不同值。
|
||||||
|
|
||||||
|
Python 中存在多个库,以简化概率推理过程。我们将查看库 `pomegranate`,看看如何在代码中表示上述数据。
|
||||||
|
|
||||||
```python
|
```python
|
||||||
from pomegranate import *
|
from pomegranate import *
|
||||||
@@ -259,15 +280,15 @@ for node, prediction in zip(model.states, predictions):
|
|||||||
print(f" {value}: {probability:.4f}")
|
print(f" {value}: {probability:.4f}")
|
||||||
```
|
```
|
||||||
|
|
||||||
- 上面的代码使用了枚举推理。然而,这种计算概率的方法效率很低,尤其是当模型中有很多变量时。另一种方法是放弃精确推理,转而采用近似推理。这样做,我们在生成的概率中会失去一些精度,但这种不精确性通常可以忽略不计。相反,我们获得了一种可扩展的概率计算方法。
|
上面的代码使用了枚举推理。然而,这种计算概率的方法效率很低,尤其是当模型中有很多变量时。另一种方法是放弃精确推理,转而采用近似推理。这样做,我们在生成的概率中会失去一些精度,但这种不精确性通常可以忽略不计。相反,我们获得了一种可扩展的概率计算方法。
|
||||||
|
|
||||||
### 采样 (Sampling)
|
### 采样 (Sampling)
|
||||||
|
|
||||||
- 采样是一种近似推理技术。在采样中,根据每个变量的概率分布对其值进行采样。
|
采样是一种近似推理技术。在采样中,根据每个变量的概率分布对其值进行采样。
|
||||||
|
|
||||||
> 要使用骰子采样生成分布,我们可以多次掷骰子,并记录每次获得的值。假设我们把骰子掷了 600 次。我们计算得到 1 的次数,应该大约是 100,然后对其余的值 2-6 重复采样。然后,我们将每个计数除以投掷的总数。这将生成掷骰子的值的近似分布:一方面,我们不太可能得到每个值发生概率为 1/6 的结果(这是确切的概率),但我们会得到一个接近它的值。
|
> 要使用骰子采样生成分布,我们可以多次掷骰子,并记录每次获得的值。假设我们把骰子掷了 600 次。我们计算得到 1 的次数,应该大约是 100,然后对其余的值 2-6 重复采样。然后,我们将每个计数除以投掷的总数。这将生成掷骰子的值的近似分布:一方面,我们不太可能得到每个值发生概率为 1/6 的结果(这是确切的概率),但我们会得到一个接近它的值。
|
||||||
|
|
||||||
- 如果我们从对 Rain 变量进行采样开始,则生成的值 none 的概率为 0.7,生成的值 light 的概率为 0.2,而生成的值 heavy 的概率则为 0.1。假设我们的采样值为 none。当我们得到 Maintenance 变量时,我们也会对其进行采样,但只能从 Rain 等于 none 的概率分布中进行采样,因为这是一个已经采样的结果。我们将通过所有节点继续这样做。现在我们有一个样本,多次重复这个过程会生成一个分布。现在,如果我们想回答一个问题,比如什么是$P(Train=on\ time)$,我们可以计算变量 Train 具有准时值的样本数量,并将结果除以样本总数。通过这种方式,我们刚刚生成了$P(Train=on\ {time})$的近似概率。
|
如果我们从对 Rain 变量进行采样开始,则生成的值 none 的概率为 0.7,生成的值 light 的概率为 0.2,而生成的值 heavy 的概率则为 0.1。假设我们的采样值为 none。当我们得到 Maintenance 变量时,我们也会对其进行采样,但只能从 Rain 等于 none 的概率分布中进行采样,因为这是一个已经采样的结果。我们将通过所有节点继续这样做。现在我们有一个样本,多次重复这个过程会生成一个分布。现在,如果我们想回答一个问题,比如什么是$P(Train=on\ time)$,我们可以计算变量 Train 具有准时值的样本数量,并将结果除以样本总数。通过这种方式,我们刚刚生成了$P(Train=on\ {time})$的近似概率。
|
||||||
|
|
||||||
<table>
|
<table>
|
||||||
<tr>
|
<tr>
|
||||||
@@ -276,7 +297,7 @@ for node, prediction in zip(model.states, predictions):
|
|||||||
</tr>
|
</tr>
|
||||||
</table>
|
</table>
|
||||||
|
|
||||||
- 我们也可以回答涉及条件概率的问题,例如$P(rain=light|train=on\ {time})$。在这种情况下,我们忽略 Train 值为 delay 的所有样本,然后照常进行。我们计算在$Train=\text{on time}$的样本中有多少样本具有变量$Rain=light$,然后除以$Train=\text{on time}$的样本总数。
|
我们也可以回答涉及条件概率的问题,例如$P(rain=light|train=on\ {time})$。在这种情况下,我们忽略 Train 值为 delay 的所有样本,然后照常进行。我们计算在$Train=\text{on time}$的样本中有多少样本具有变量$Rain=light$,然后除以$Train=\text{on time}$的样本总数。
|
||||||
|
|
||||||
<table>
|
<table>
|
||||||
<tr>
|
<tr>
|
||||||
@@ -289,7 +310,7 @@ for node, prediction in zip(model.states, predictions):
|
|||||||
| --------------------- | ------------------ |
|
| --------------------- | ------------------ |
|
||||||
|  |  |
|
|  |  |
|
||||||
|
|
||||||
- 在代码中,采样函数可以是 `generate_sample`:
|
在代码中,采样函数可以是 `generate_sample`:
|
||||||
|
|
||||||
```python
|
```python
|
||||||
'''如果你对 pomegrante 库不熟悉,没有关系,考虑 generate_sample 为一个黑盒,或者你可以在 python 解释器中查看 model.states, state.distribution 的值以了解 model 在该库中的实现方式'''
|
'''如果你对 pomegrante 库不熟悉,没有关系,考虑 generate_sample 为一个黑盒,或者你可以在 python 解释器中查看 model.states, state.distribution 的值以了解 model 在该库中的实现方式'''
|
||||||
@@ -329,33 +350,35 @@ print(Counter(data))
|
|||||||
|
|
||||||
### 似然加权
|
### 似然加权
|
||||||
|
|
||||||
- 在上面的采样示例中,我们丢弃了与我们所掌握的证据不匹配的样本。这是低效的。解决这一问题的一种方法是使用似然加权,使用以下步骤:
|
在上面的采样示例中,我们丢弃了与我们所掌握的证据不匹配的样本。这是低效的。解决这一问题的一种方法是使用似然加权,使用以下步骤:
|
||||||
|
|
||||||
- 首先固定证据变量的值。
|
- 首先固定证据变量的值。
|
||||||
- 使用贝叶斯网络中的条件概率对非证据变量进行采样。
|
- 使用贝叶斯网络中的条件概率对非证据变量进行采样。
|
||||||
- 根据其可能性对每个样本进行加权:所有证据出现的概率。
|
- 根据其可能性对每个样本进行加权:所有证据出现的概率。
|
||||||
- 例如,如果我们观察到$Train=\text{on time}$,我们将像之前一样开始采样。我们对给定概率分布的 Rain 值进行采样,然后对 Maintenance 进行采样,但当我们到达 Train 时,我们总是按照观测值取值。然后,我们继续进行,并在给定$Train=\text{on time}$的情况下,根据其概率分布对 Appointment 进行采样。既然这个样本存在,我们就根据观察到的变量在给定其采样父变量的情况下的条件概率对其进行加权。也就是说,如果我们采样了 Rain 并得到了 light,然后我们采样了 Maintenance 并得到了 yes,那么我们将用$P(Train=\text{on time}|light,yes)$来加权这个样本。
|
|
||||||
|
例如,如果我们观察到$Train=\text{on time}$,我们将像之前一样开始采样。我们对给定概率分布的 Rain 值进行采样,然后对 Maintenance 进行采样,但当我们到达 Train 时,我们总是按照观测值取值。然后,我们继续进行,并在给定$Train=\text{on time}$的情况下,根据其概率分布对 Appointment 进行采样。既然这个样本存在,我们就根据观察到的变量在给定其采样父变量的情况下的条件概率对其进行加权。也就是说,如果我们采样了 Rain 并得到了 light,然后我们采样了 Maintenance 并得到了 yes,那么我们将用$P(Train=\text{on time}|light,yes)$来加权这个样本。
|
||||||
|
|
||||||
## 马尔科夫模型 (Markov Models)
|
## 马尔科夫模型 (Markov Models)
|
||||||
|
|
||||||
- 到目前为止,我们已经研究了概率问题,给出了我们观察到的一些信息。在这种范式中,时间的维度没有以任何方式表示。然而,许多任务确实依赖于时间维度,例如预测。为了表示时间变量,我们将创建一个新的变量$X$,并根据感兴趣的事件对其进行更改,使$X_t$ 是当前事件,$X_{t+1}$ 是下一个事件,依此类推。为了能够预测未来的事件,我们将使用马尔可夫模型。
|
到目前为止,我们已经研究了概率问题,给出了我们观察到的一些信息。在这种范式中,时间的维度没有以任何方式表示。然而,许多任务确实依赖于时间维度,例如预测。为了表示时间变量,我们将创建一个新的变量$X$,并根据感兴趣的事件对其进行更改,使$X_t$ 是当前事件,$X_{t+1}$ 是下一个事件,依此类推。为了能够预测未来的事件,我们将使用马尔可夫模型。
|
||||||
|
|
||||||
### 马尔科夫假设 (**The Markov Assumption**)
|
### 马尔科夫假设 (**The Markov Assumption**)
|
||||||
|
|
||||||
- 马尔科夫假设是一个假设,即当前状态只取决于有限的固定数量的先前状态。想想预测天气的任务。在理论上,我们可以使用过去一年的所有数据来预测明天的天气。然而,这是不可行的,一方面是因为这需要计算能力,另一方面是因为可能没有关于基于 365 天前天气的明天天气的条件概率的信息。使用马尔科夫假设,我们限制了我们以前的状态(例如,在预测明天的天气时,我们要考虑多少个以前的日子),从而使这个任务变得可控。这意味着我们可能会得到感兴趣的概率的一个更粗略的近似值,但这往往足以满足我们的需要。此外,我们可以根据最后一个事件的信息来使用马尔可夫模型(例如,根据今天的天气来预测明天的天气)。
|
马尔科夫假设是一个假设,即当前状态只取决于有限的固定数量的先前状态。想想预测天气的任务。在理论上,我们可以使用过去一年的所有数据来预测明天的天气。然而,这是不可行的,一方面是因为这需要计算能力,另一方面是因为可能没有关于基于 365 天前天气的明天天气的条件概率的信息。使用马尔科夫假设,我们限制了我们以前的状态(例如,在预测明天的天气时,我们要考虑多少个以前的日子),从而使这个任务变得可控。这意味着我们可能会得到感兴趣的概率的一个更粗略的近似值,但这往往足以满足我们的需要。此外,我们可以根据最后一个事件的信息来使用马尔可夫模型(例如,根据今天的天气来预测明天的天气)。
|
||||||
|
|
||||||
### 马尔科夫链 (**Markov Chain**)
|
### 马尔科夫链 (**Markov Chain**)
|
||||||
|
|
||||||
- 马尔科夫链是一个随机变量的序列,每个变量的分布都遵循马尔科夫假设。也就是说,链中的每个事件的发生都是基于之前事件的概率。
|
马尔科夫链是一个随机变量的序列,每个变量的分布都遵循马尔科夫假设。也就是说,链中的每个事件的发生都是基于之前事件的概率。
|
||||||
- 为了构建马尔可夫链,我们需要一个过渡模型,该模型将根据当前事件的可能值来指定下一个事件的概率分布。
|
|
||||||
|
为了构建马尔可夫链,我们需要一个过渡模型,该模型将根据当前事件的可能值来指定下一个事件的概率分布。
|
||||||
|
|
||||||
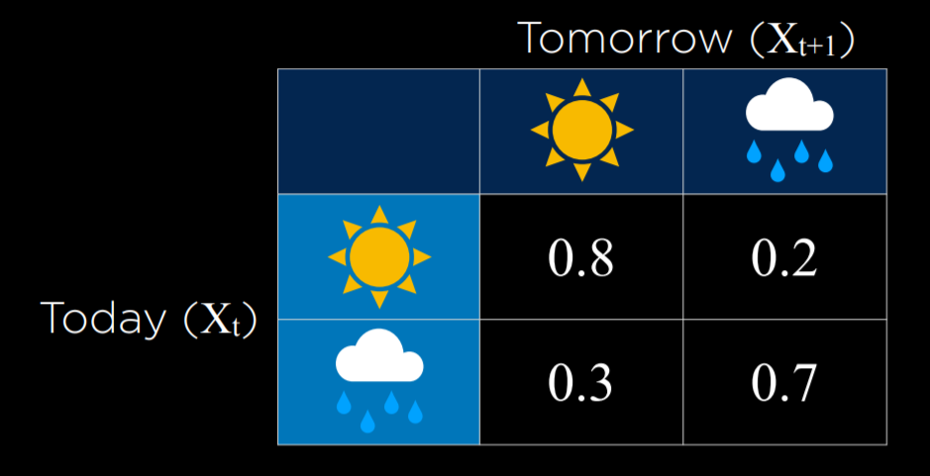
|

|
||||||
|
|
||||||
- 在这个例子中,基于今天是晴天,明天是晴天的概率是 0.8。这是合理的,因为晴天之后更可能是晴天。然而,如果今天是雨天,明天下雨的概率是 0.7,因为雨天更有可能相继出现。使用这个过渡模型,可以对马尔可夫链进行采样。从一天是雨天或晴天开始,然后根据今天的天气,对第二天的晴天或雨天的概率进行采样。然后,根据明天的情况对后天的概率进行采样,以此类推,形成马尔科夫链:
|
在这个例子中,基于今天是晴天,明天是晴天的概率是 0.8。这是合理的,因为晴天之后更可能是晴天。然而,如果今天是雨天,明天下雨的概率是 0.7,因为雨天更有可能相继出现。使用这个过渡模型,可以对马尔可夫链进行采样。从一天是雨天或晴天开始,然后根据今天的天气,对第二天的晴天或雨天的概率进行采样。然后,根据明天的情况对后天的概率进行采样,以此类推,形成马尔科夫链:
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
- 给定这个马尔可夫链,我们现在可以回答诸如“连续四个雨天的概率是多少?”这样的问题。下面是一个如何在代码中实现马尔可夫链的例子:
|
给定这个马尔可夫链,我们现在可以回答诸如“连续四个雨天的概率是多少?”这样的问题。下面是一个如何在代码中实现马尔可夫链的例子:
|
||||||
|
|
||||||
```python
|
```python
|
||||||
from pomegranate import *
|
from pomegranate import *
|
||||||
@@ -379,31 +402,36 @@ print(model.sample(50))
|
|||||||
|
|
||||||
## 隐马尔科夫模型 (Hidden Markov Models)
|
## 隐马尔科夫模型 (Hidden Markov Models)
|
||||||
|
|
||||||
- 隐马尔科夫模型是一种具有隐藏状态的系统的马尔科夫模型,它产生了一些观察到的事件。这意味着,有时候,人工智能对世界有一些测量,但无法获得世界的精确状态。在这些情况下,世界的状态被称为隐藏状态,而人工智能能够获得的任何数据都是观察结果。下面是一些这方面的例子:
|
隐马尔科夫模型是一种具有隐藏状态的系统的马尔科夫模型,它产生了一些观察到的事件。这意味着,有时候,人工智能对世界有一些测量,但无法获得世界的精确状态。在这些情况下,世界的状态被称为隐藏状态,而人工智能能够获得的任何数据都是观察结果。下面是一些这方面的例子:
|
||||||
|
|
||||||
- 对于一个探索未知领域的机器人来说,隐藏状态是它的位置,而观察是机器人的传感器所记录的数据。
|
- 对于一个探索未知领域的机器人来说,隐藏状态是它的位置,而观察是机器人的传感器所记录的数据。
|
||||||
- 在语音识别中,隐藏状态是所讲的话语,而观察是音频波形。
|
- 在语音识别中,隐藏状态是所讲的话语,而观察是音频波形。
|
||||||
- 在衡量网站的用户参与度时,隐藏的状态是用户的参与程度,而观察是网站或应用程序的分析。
|
- 在衡量网站的用户参与度时,隐藏的状态是用户的参与程度,而观察是网站或应用程序的分析。
|
||||||
- 举个例子。我们的人工智能想要推断天气 (隐藏状态),但它只能接触到一个室内摄像头,记录有多少人带了雨伞。这里是我们的传感器模型 (sensor model),表示了这些概率:
|
|
||||||
|
举个例子。我们的人工智能想要推断天气 (隐藏状态),但它只能接触到一个室内摄像头,记录有多少人带了雨伞。这里是我们的传感器模型 (sensor model),表示了这些概率:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 在这个模型中,如果是晴天,人们很可能不会带伞到大楼。如果是雨天,那么人们就很有可能带伞到大楼来。通过对人们是否带伞的观察,我们可以合理地预测外面的天气情况。
|
在这个模型中,如果是晴天,人们很可能不会带伞到大楼。如果是雨天,那么人们就很有可能带伞到大楼来。通过对人们是否带伞的观察,我们可以合理地预测外面的天气情况。
|
||||||
|
|
||||||
### 传感器马尔科夫假设
|
### 传感器马尔科夫假设
|
||||||
|
|
||||||
- 假设证据变量只取决于相应的状态。例如,对于我们的模型,我们假设人们是否带雨伞去办公室只取决于天气。这不一定反映了完整的事实,因为,比如说,比较自觉的、不喜欢下雨的人可能即使在阳光明媚的时候也会到处带伞,如果我们知道每个人的个性,会给模型增加更多的数据。然而,传感器马尔科夫假设忽略了这些数据,假设只有隐藏状态会影响观察。
|
假设证据变量只取决于相应的状态。例如,对于我们的模型,我们假设人们是否带雨伞去办公室只取决于天气。这不一定反映了完整的事实,因为,比如说,比较自觉的、不喜欢下雨的人可能即使在阳光明媚的时候也会到处带伞,如果我们知道每个人的个性,会给模型增加更多的数据。然而,传感器马尔科夫假设忽略了这些数据,假设只有隐藏状态会影响观察。
|
||||||
- 隐马尔科夫模型可以用一个有两层的马尔科夫链来表示。上层,变量$X$,代表隐藏状态。底层,变量$E$,代表证据,即我们所拥有的观察。
|
|
||||||
|
隐马尔科夫模型可以用一个有两层的马尔科夫链来表示。上层,变量$X$,代表隐藏状态。底层,变量$E$,代表证据,即我们所拥有的观察。
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
- 基于隐马尔科夫模型,可以实现多种任务:
|
基于隐马尔科夫模型,可以实现多种任务:
|
||||||
|
|
||||||
- 筛选 Filtering: 给定从开始到现在的观察结果,计算出**当前**状态的概率分布。例如,给从从特定时间开始到今天人们带伞的信息,我们产生一个今天是否下雨的概率分布。
|
- 筛选 Filtering: 给定从开始到现在的观察结果,计算出<strong>当前</strong>状态的概率分布。例如,给从从特定时间开始到今天人们带伞的信息,我们产生一个今天是否下雨的概率分布。
|
||||||
- 预测 Prediction: 给定从开始到现在的观察,计算**未来**状态的概率分布。
|
- 预测 Prediction: 给定从开始到现在的观察,计算<strong>未来</strong>状态的概率分布。
|
||||||
- 平滑化 Smoothing: 给定从开始到现在的观察,计算**过去**状态的概率分布。例如,鉴于今天人们带了雨伞,计算昨天下雨的概率。
|
- 平滑化 Smoothing: 给定从开始到现在的观察,计算<strong>过去</strong>状态的概率分布。例如,鉴于今天人们带了雨伞,计算昨天下雨的概率。
|
||||||
- 最可能的解释 Most likely explanation: 鉴于从开始到现在的观察,计算最可能的事件顺序。
|
- 最可能的解释 Most likely explanation: 鉴于从开始到现在的观察,计算最可能的事件顺序。
|
||||||
- 最可能的解释任务可用于语音识别等过程,根据多个波形,人工智能推断出给这些波形带来的最有可能的单词或音节的序列。接下来是一个隐马尔科夫模型的 Python 实现,我们将用于最可能的解释任务:
|
|
||||||
|
最可能的解释任务可用于语音识别等过程,根据多个波形,人工智能推断出给这些波形带来的最有可能的单词或音节的序列。
|
||||||
|
|
||||||
|
接下来是一个隐马尔科夫模型的 Python 实现,我们将用于最可能的解释任务:
|
||||||
|
|
||||||
```python
|
```python
|
||||||
from pomegranate import *
|
from pomegranate import *
|
||||||
@@ -432,7 +460,7 @@ model = HiddenMarkovModel.from_matrix(
|
|||||||
model.bake()
|
model.bake()
|
||||||
```
|
```
|
||||||
|
|
||||||
- 请注意,我们的模型同时具有传感器模型和过渡模型。对于隐马尔可夫模型,我们需要这两个模型。在下面的代码片段中,我们看到了人们是否带伞到大楼的观察序列,根据这个序列,我们将运行模型,它将生成并打印出最可能的解释 (即最可能带来这种观察模式的天气序列):
|
请注意,我们的模型同时具有传感器模型和过渡模型。对于隐马尔可夫模型,我们需要这两个模型。在下面的代码片段中,我们看到了人们是否带伞到大楼的观察序列,根据这个序列,我们将运行模型,它将生成并打印出最可能的解释 (即最可能带来这种观察模式的天气序列):
|
||||||
|
|
||||||
```python
|
```python
|
||||||
from model import model
|
from model import model
|
||||||
@@ -454,4 +482,4 @@ for prediction in predictions:
|
|||||||
print(model.states[prediction].name)
|
print(model.states[prediction].name)
|
||||||
```
|
```
|
||||||
|
|
||||||
- 在这种情况下,程序的输出将是 rain,rain,sun,rain,rain,rain,rain,sun,sun。根据我们对人们带伞或不带伞到大楼的观察,这一输出代表了最有可能的天气模式。
|
在这种情况下,程序的输出将是 rain,rain,sun,rain,rain,rain,rain,sun,sun。根据我们对人们带伞或不带伞到大楼的观察,这一输出代表了最有可能的天气模式。
|
||||||
|
|||||||
@@ -29,55 +29,58 @@ $ python generate.py data/structure1.txt data/words1.txt output.png
|
|||||||
|
|
||||||
## 背景
|
## 背景
|
||||||
|
|
||||||
- 你如何生成一个填字游戏?考虑到填字游戏的结构(即网格中哪些方格需要填入字母),以及要使用的单词列表,问题就变成了选择哪些单词应该填入每个垂直或水平的方格序列。我们可以将这种问题建模为一个约束满足问题。每一个方格序列都是一个变量,我们需要决定它的值(在可能的单词域中哪个单词将被填入该序列)。考虑一下下面的字谜结构。
|
你如何生成一个填字游戏?考虑到填字游戏的结构(即网格中哪些方格需要填入字母),以及要使用的单词列表,问题就变成了选择哪些单词应该填入每个垂直或水平的方格序列。我们可以将这种问题建模为一个约束满足问题。每一个方格序列都是一个变量,我们需要决定它的值(在可能的单词域中哪个单词将被填入该序列)。考虑一下下面的字谜结构。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 在这个结构中,我们有四个变量,代表了我们需要填入这个字谜的四个单词(在上图中每个单词都用数字表示)。每个变量由四个值定义:它开始的行(`i`值),它开始的列(`j`值),单词的方向(纵向或横向down or across),以及单词的长度。例如,`变量1`将是一个由第1行(假设从顶部计数的0索引)、第1列(假设从左边计数的0索引)、方向为`across`和`4`的长度表示的变量。
|
在这个结构中,我们有四个变量,代表了我们需要填入这个字谜的四个单词(在上图中每个单词都用数字表示)。每个变量由四个值定义:它开始的行(`i`值),它开始的列(`j`值),单词的方向(纵向或横向down or across),以及单词的长度。例如,`变量1`将是一个由第1行(假设从顶部计数的0索引)、第1列(假设从左边计数的0索引)、方向为`across`和`4`的长度表示的变量。
|
||||||
|
|
||||||
- 与许多约束满足问题一样,这些变量有一元和二元约束。变量的一元约束是由其长度决定的。例如,对于`变量1`来说,数值`BYTE`可以满足一元约束,但是数值`BIT`则不能(它有错误的字母数量)。因此,任何不满足变量的一元约束的值都可以立即从变量的域中删除。
|
与许多约束满足问题一样,这些变量有一元和二元约束。变量的一元约束是由其长度决定的。例如,对于`变量1`来说,数值`BYTE`可以满足一元约束,但是数值`BIT`则不能(它有错误的字母数量)。因此,任何不满足变量的一元约束的值都可以立即从变量的域中删除。
|
||||||
|
|
||||||
- 变量的二元约束是由其与相邻变量的重合度给出的。`变量1`有一个邻居:`变量2`。`变量2`有两个邻居:`变量1`和`变量3`。对于每一对相邻的变量,这些变量都有一个重叠部分:一个它们共同的单方块。我们可以将这种重叠表示为每个变量有用相同字符位置的索引对。例如,`变量1`和`变量2`之间的重叠可以表示为一对`(1, 0)`,这意味着`变量1`在索引1处的字符必然与`变量2`在索引0处的字符相同(再次假设索引从0开始)。因此,`变量2`和`变量3`之间的重叠将被表示为一对`(3, 1)`,`变量2`的值的字符`3`必须与`变量3`的值的字符`1`相同。
|
变量的二元约束是由其与相邻变量的重合度给出的。`变量1`有一个邻居:`变量2`。`变量2`有两个邻居:`变量1`和`变量3`。对于每一对相邻的变量,这些变量都有一个重叠部分:一个它们共同的单方块。我们可以将这种重叠表示为每个变量有用相同字符位置的索引对。例如,`变量1`和`变量2`之间的重叠可以表示为一对`(1, 0)`,这意味着`变量1`在索引1处的字符必然与`变量2`在索引0处的字符相同(再次假设索引从0开始)。因此,`变量2`和`变量3`之间的重叠将被表示为一对`(3, 1)`,`变量2`的值的字符`3`必须与`变量3`的值的字符`1`相同。
|
||||||
|
|
||||||
- 对于这个问题,我们将增加一个额外的约束条件,即所有的单词必须是不同的:同一个单词不应该在谜题中重复出现多次。
|
对于这个问题,我们将增加一个额外的约束条件,即所有的单词必须是不同的:同一个单词不应该在谜题中重复出现多次。
|
||||||
|
|
||||||
- 那么,接下来的挑战是写一个程序来找到一个满意的赋值:为每个变量提供一个不同的词(来自给定的词汇表),从而满足所有的一元和二元约束。
|
那么,接下来的挑战是写一个程序来找到一个满意的赋值:为每个变量提供一个不同的词(来自给定的词汇表),从而满足所有的一元和二元约束。
|
||||||
理解
|
|
||||||
|
|
||||||
- 这个项目中有两个Python文件:`crossword.py`和`generate.py`。第一个文件已经完全为你写好了,第二个文件有一些函数留给你去实现。
|
## 理解
|
||||||
|
|
||||||
- 首先,让我们看一下`crossword.py`。这个文件定义了两个类,`Variable`(代表填字游戏中的变量)和`Crossword`(代表填字游戏本身)。
|
这个项目中有两个Python文件:`crossword.py`和`generate.py`。第一个文件已经完全为你写好了,第二个文件有一些函数留给你去实现。
|
||||||
|
|
||||||
- 注意,要创建一个变量,我们必须指定四个值:它的第`i`行,第`j`列,它的方向(常数`Variable.ACROSS`或常数`Variable.DOWN``),以及它的长度(`length``)。
|
首先,让我们看一下`crossword.py`。这个文件定义了两个类,`Variable`(代表填字游戏中的变量)和`Crossword`(代表填字游戏本身)。
|
||||||
|
|
||||||
- 字谜类需要两个值来创建一个新的字谜:一个定义了字谜结构的`structure_file`(`_`用来代表空白单元格,任何其他字符都代表不会被填入的单元格)和一个定义了字词列表(每行一个)的`word_file`,用来作为游戏的词汇表。这些文件的三个例子可以在项目的数据目录中找到,也欢迎你自己创建。
|
注意,要创建一个变量,我们必须指定四个值:它的第`i`行,第`j`列,它的方向(常数`Variable.ACROSS`或常数`Variable.DOWN``),以及它的长度(`length``)。
|
||||||
|
|
||||||
- 特别要注意的是,对于任何一个字谜对象的字谜,我们都会存储以下的数值:
|
字谜类需要两个值来创建一个新的字谜:一个定义了字谜结构的`structure_file`(`_`用来代表空白单元格,任何其他字符都代表不会被填入的单元格)和一个定义了字词列表(每行一个)的`word_file`,用来作为游戏的词汇表。这些文件的三个例子可以在项目的数据目录中找到,也欢迎你自己创建。
|
||||||
- `crossword.height`是一个整数,代表填字游戏的高度。
|
|
||||||
- `crossword.width`是一个整数,代表填字游戏的宽度。
|
|
||||||
- `crossword.structure`是一个二维列表,代表字谜的结构。对于任何有效的第i行和第j列,如果该单元格是空白的,`crossword.structure[i][j]`将为真(必须在该单元格中填入一个字符),否则将为假(该单元格中没有字符要填)。
|
|
||||||
- `crossword.words`是一个包含所有单词的集合,在构建填字游戏的时候,可以从这些单词中提取。
|
|
||||||
- `crossword.variables`是谜题中所有变量的集合(每个变量都是一个Variable对象)。
|
|
||||||
- `crossword.overlaps`是一个字典,它将一对变量映射到它们的重合处。对于任何两个不同的变量v1和v2,如果这两个变量没有重叠,`crossword.overlaps[v1, v2]`将是`None`,如果这两个变量有重叠,则是一对整数`(i, j)`。这对`(i, j)`应被解释为:`v1`的第`i`个字符的值必须与`v2`的第`j`个字符的值相同。
|
|
||||||
|
|
||||||
- `Crossword`对象还支持一个方法`neighbors`,它可以返回与给定变量重叠的所有变量。也就是说,`crossword.neighbors(v1)`将返回一个与变量`v1`相邻的所有变量的集合。
|
特别要注意的是,对于任何一个字谜对象的字谜,我们都会存储以下的数值:
|
||||||
|
|
||||||
- 接下来,看一下`generate.py`。在这里,我们定义了一个`CrosswordCreator`类,我们将用它来解决填字游戏。当一个`CrosswordCreator`对象被创建时,它得到一个填字游戏的属性,它应该是一个`Crossword`对象(因此具有上面描述的所有属性)。每个`CrosswordCreator`对象还得到一个域属性:一个字典,它将变量映射到该变量可能作为一个值的一组词。最初,这组词是我们词汇表中的所有词,但我们很快就会写函数来限制这些域。
|
- `crossword.height`是一个整数,代表填字游戏的高度。
|
||||||
|
- `crossword.width`是一个整数,代表填字游戏的宽度。
|
||||||
|
- `crossword.structure`是一个二维列表,代表字谜的结构。对于任何有效的第i行和第j列,如果该单元格是空白的,`crossword.structure[i][j]`将为真(必须在该单元格中填入一个字符),否则将为假(该单元格中没有字符要填)。
|
||||||
|
- `crossword.words`是一个包含所有单词的集合,在构建填字游戏的时候,可以从这些单词中提取。
|
||||||
|
- `crossword.variables`是谜题中所有变量的集合(每个变量都是一个Variable对象)。
|
||||||
|
- `crossword.overlaps`是一个字典,它将一对变量映射到它们的重合处。对于任何两个不同的变量v1和v2,如果这两个变量没有重叠,`crossword.overlaps[v1, v2]`将是`None`,如果这两个变量有重叠,则是一对整数`(i, j)`。这对`(i, j)`应被解释为:`v1`的第`i`个字符的值必须与`v2`的第`j`个字符的值相同。
|
||||||
|
|
||||||
- 我们还为你定义了一些函数,以帮助你测试你的代码:`print`将向终端打印你的填字游戏的一个给定的赋值(每个赋值,在这个函数和其他地方,是一个字典,将变量映射到它们相应的词)。同时,`save`将生成一个与给定作业相对应的图像文件(如果你无法使用这个函数,你需要`pip3 install Pillow`)。 `letter_grid`是一个被`print`和`save`使用的辅助函数,它为给定的赋值生成一个所有字符在其适当位置的2D列表:你可能不需要自己调用这个函数,但如果你想的话,欢迎你这样做。
|
`Crossword`对象还支持一个方法`neighbors`,它可以返回与给定变量重叠的所有变量。也就是说,`crossword.neighbors(v1)`将返回一个与变量`v1`相邻的所有变量的集合。
|
||||||
|
|
||||||
- 最后,注意`solve`函数。这个函数做了三件事:首先,它调用`enforce_node_consistency`来强制执行填字游戏的节点一致性,确保变量域中的每个值都满足一元约束。接下来,该函数调用`ac3`来强制执行弧一致性,确保二元约束得到满足。最后,该函数在最初的空赋值(空字典dict())上调用`backtrack`,试图计算出问题的解决方案。
|
接下来,看一下`generate.py`。在这里,我们定义了一个`CrosswordCreator`类,我们将用它来解决填字游戏。当一个`CrosswordCreator`对象被创建时,它得到一个填字游戏的属性,它应该是一个`Crossword`对象(因此具有上面描述的所有属性)。每个`CrosswordCreator`对象还得到一个域属性:一个字典,它将变量映射到该变量可能作为一个值的一组词。最初,这组词是我们词汇表中的所有词,但我们很快就会写函数来限制这些域。
|
||||||
|
|
||||||
- 不过,`enforce_node_consistency`、`ac3`和`backtrack`等函数还没有实现(以及其他函数)。这就是你的任务。
|
我们还为你定义了一些函数,以帮助你测试你的代码:`print`将向终端打印你的填字游戏的一个给定的赋值(每个赋值,在这个函数和其他地方,是一个字典,将变量映射到它们相应的词)。同时,`save`将生成一个与给定作业相对应的图像文件(如果你无法使用这个函数,你需要`pip3 install Pillow`)。 `letter_grid`是一个被`print`和`save`使用的辅助函数,它为给定的赋值生成一个所有字符在其适当位置的2D列表:你可能不需要自己调用这个函数,但如果你想的话,欢迎你这样做。
|
||||||
|
|
||||||
|
最后,注意`solve`函数。这个函数做了三件事:首先,它调用`enforce_node_consistency`来强制执行填字游戏的节点一致性,确保变量域中的每个值都满足一元约束。接下来,该函数调用`ac3`来强制执行弧一致性,确保二元约束得到满足。最后,该函数在最初的空赋值(空字典dict())上调用`backtrack`,试图计算出问题的解决方案。
|
||||||
|
|
||||||
|
不过,`enforce_node_consistency`、`ac3`和`backtrack`等函数还没有实现(以及其他函数)。这就是你的任务。
|
||||||
|
|
||||||
## 明确
|
## 明确
|
||||||
|
|
||||||
- 完成`grece_node_consistency`, `revise`, `ac3`, `assignment_complete`, `consistent`, `order_domain_values`, `selected_unassigned_variable`和`backtrack`在`generate.py`中的实现,这样如果有有解的话你的人工智能就能生成完整的字谜。
|
完成`grece_node_consistency`, `revise`, `ac3`, `assignment_complete`, `consistent`, `order_domain_values`, `selected_unassigned_variable`和`backtrack`在`generate.py`中的实现,这样如果有有解的话你的人工智能就能生成完整的字谜。
|
||||||
|
|
||||||
- `enforce_node_consistency`函数应该更新`self.domains`,使每个变量都是节点一致的。
|
- `enforce_node_consistency`函数应该更新`self.domains`,使每个变量都是节点一致的。
|
||||||
- 回顾一下,当对每个变量来说,其域中的每个值都与该变量的一元约束一致时,就实现了节点一致性。在填字游戏的情况下,这意味着要确保变量域中的每个值的字母数与变量的长度相同。
|
- 回顾一下,当对每个变量来说,其域中的每个值都与该变量的一元约束一致时,就实现了节点一致性。在填字游戏的情况下,这意味着要确保变量域中的每个值的字母数与变量的长度相同。
|
||||||
- 要从一个变量`v`的域中移除一个值`x`,因为`self.domains`是一个将变量映射到数值集的字典,你可以调用`self.domains[v].remove(x)`。
|
- 要从一个变量`v`的域中移除一个值`x`,因为`self.domains`是一个将变量映射到数值集的字典,你可以调用`self.domains[v].remove(x)`。
|
||||||
- 这个函数不需要返回值。
|
- 这个函数不需要返回值。
|
||||||
|
|
||||||
- `revise`函数应该使变量x与变量y保持弧一致性。
|
- `revise`函数应该使变量x与变量y保持弧一致性。
|
||||||
- `x`和`y`都是`Variable`对象,代表谜题中的变量。
|
- `x`和`y`都是`Variable`对象,代表谜题中的变量。
|
||||||
- 回顾一下,当`x`的域中的每一个值在`y`的域中都有一个不引起冲突的可能值时,`x`就与`y`保持弧一致性。(在填字游戏的背景下,冲突是指一个方格,两个变量对它的字符值意见不一)。
|
- 回顾一下,当`x`的域中的每一个值在`y`的域中都有一个不引起冲突的可能值时,`x`就与`y`保持弧一致性。(在填字游戏的背景下,冲突是指一个方格,两个变量对它的字符值意见不一)。
|
||||||
@@ -123,7 +126,7 @@ $ python generate.py data/structure1.txt data/words1.txt output.png
|
|||||||
- 如果有可能生成一个令人满意的字谜,你的函数应该返回完整的赋值:一个字典,其中每个变量是一个键,值是该变量应该承担的单词。如果不可能产生令人满意的赋值,该函数应该返回`None`。
|
- 如果有可能生成一个令人满意的字谜,你的函数应该返回完整的赋值:一个字典,其中每个变量是一个键,值是该变量应该承担的单词。如果不可能产生令人满意的赋值,该函数应该返回`None`。
|
||||||
- 如果你愿意,你可能会发现,如果你把搜索和推理交织在一起,你的算法会更有效率(比如每次做新的赋值时都要保持弧一致性)。我们不要求你这样做,但允许你这样做,只要你的函数仍然产生正确的结果。(正是由于这个原因,`ac3`函数允许一个`arcs`的参数,以防你想从不同的弧队列开始)。
|
- 如果你愿意,你可能会发现,如果你把搜索和推理交织在一起,你的算法会更有效率(比如每次做新的赋值时都要保持弧一致性)。我们不要求你这样做,但允许你这样做,只要你的函数仍然产生正确的结果。(正是由于这个原因,`ac3`函数允许一个`arcs`的参数,以防你想从不同的弧队列开始)。
|
||||||
|
|
||||||
- 除了要求你实现的函数外,你不应该修改`generate.py`中的任何其他东西,尽管你可以编写额外的函数和/或导入其他Python标准库模块。如果你熟悉`numpy`或`pandas`,你也可以导入它们,但是你不应该使用任何其他的第三方Python模块。你不应该修改`crossword.py`中的任何东西。
|
除了要求你实现的函数外,你不应该修改`generate.py`中的任何其他东西,尽管你可以编写额外的函数和/或导入其他Python标准库模块。如果你熟悉`numpy`或`pandas`,你也可以导入它们,但是你不应该使用任何其他的第三方Python模块。你不应该修改`crossword.py`中的任何东西。
|
||||||
|
|
||||||
## 提示
|
## 提示
|
||||||
|
|
||||||
|
|||||||
@@ -1,32 +1,33 @@
|
|||||||
# 最优化
|
# 最优化
|
||||||
|
|
||||||
- 最优化是指从一组可能的选项中选择最佳选项。我们已经遇到过试图找到最佳选项的问题,比如在极大极小算法中,今天我们将学习一些工具,可以用来解决更广泛的问题。
|
最优化是指从一组可能的选项中选择最佳选项。我们已经遇到过试图找到最佳选项的问题,比如在极大极小算法中,今天我们将学习一些工具,可以用来解决更广泛的问题。
|
||||||
|
|
||||||
## 局部搜索(Local Search)
|
## 局部搜索(Local Search)
|
||||||
|
|
||||||
- 局部搜索是一种保持单一节点并通过移动到邻近的节点进行搜索的搜索算法。这种类型的算法与我们之前看到的搜索类型不同。例如,在解决迷宫的过程中,我们想找到通往目标的最快捷的方法,而局部搜索则对寻找问题的最佳答案感兴趣。通常情况下,局部搜索会带来一个不是最佳但 "足够好 "的答案,以节省计算能力。考虑一下下面这个局部搜索问题的例子:我们有四所房子在设定的位置。我们想建两所医院,使每所房子到医院的距离最小。这个问题可以形象地描述如下:
|
局部搜索是一种保持单一节点并通过移动到邻近的节点进行搜索的搜索算法。这种类型的算法与我们之前看到的搜索类型不同。例如,在解决迷宫的过程中,我们想找到通往目标的最快捷的方法,而局部搜索则对寻找问题的最佳答案感兴趣。通常情况下,局部搜索会带来一个不是最佳但 "足够好 "的答案,以节省计算能力。考虑一下下面这个局部搜索问题的例子:我们有四所房子在设定的位置。我们想建两所医院,使每所房子到医院的距离最小。这个问题可以形象地描述如下:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 在这幅图中,我们看到的是房屋和医院的可能配置。它们之间的距离是用曼哈顿距离(向上、向下和向两侧移动的次数;在[搜索](4.3.1搜索.md) 中详细讨论)来衡量的,从每个房子到最近的医院的距离之和是17。我们称其为成本 __(cost)__,因为我们试图使这个距离最小化。在这种情况下,一个状态将是房屋和医院的任何一个配置。
|
在这幅图中,我们看到的是房屋和医院的可能配置。它们之间的距离是用曼哈顿距离(向上、向下和向两侧移动的次数;在[搜索](4.3.1搜索.md) 中详细讨论)来衡量的,从每个房子到最近的医院的距离之和是17。我们称其为成本 __(cost)__,因为我们试图使这个距离最小化。在这种情况下,一个状态将是房屋和医院的任何一个配置。
|
||||||
|
|
||||||
- 把这个概念抽象化,我们可以把每一种房屋和医院的配置表现为下面的状态空间图。图中的每一条都代表一个状态的值,在我们的例子中,它是房屋和医院配置的成本。
|
把这个概念抽象化,我们可以把每一种房屋和医院的配置表现为下面的状态空间图。图中的每一条都代表一个状态的值,在我们的例子中,它是房屋和医院配置的成本。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 从这个可视化的角度来看,我们可以为我们接下来的讨论定义几个重要的术语:
|
从这个可视化的角度来看,我们可以为我们接下来的讨论定义几个重要的术语:
|
||||||
- 目标函数 __(Objective Function)__ 是一个函数,我们用它来最大化解决方案的值。
|
|
||||||
- 成本函数 __(Cost Function)__ 是一个我们用来最小化解决方案成本的函数(这就是我们在房屋和医院的例子中要使用的函数。我们想要最小化从房屋到医院的距离)。
|
|
||||||
- 当前状态 __(Current State)__ 是指函数目前正在考虑的状态。
|
|
||||||
- 邻居状态 __(Neighbor State)__ 是当前状态可以过渡到的一个状态。在上面的一维状态空间图中,邻居状态是指当前状态两侧的状态。在我们的例子中,邻居状态可以是将其中一家医院向任何方向移动一步所产生的状态。邻居状态通常与当前状态相似,因此,其值与当前状态的值接近。
|
|
||||||
|
|
||||||
- 请注意,局部搜索算法的工作方式是考虑当前状态下的一个节点,然后将该节点移动到当前状态的一个邻节点处。这与极大极小算法不同,例如,在极大极小算法中,状态空间中的每一个状态都被递归地考虑。
|
- 目标函数 __(Objective Function)__ 是一个函数,我们用它来最大化解决方案的值。
|
||||||
|
- 成本函数 __(Cost Function)__ 是一个我们用来最小化解决方案成本的函数(这就是我们在房屋和医院的例子中要使用的函数。我们想要最小化从房屋到医院的距离)。
|
||||||
|
- 当前状态 __(Current State)__ 是指函数目前正在考虑的状态。
|
||||||
|
- 邻居状态 __(Neighbor State)__ 是当前状态可以过渡到的一个状态。在上面的一维状态空间图中,邻居状态是指当前状态两侧的状态。在我们的例子中,邻居状态可以是将其中一家医院向任何方向移动一步所产生的状态。邻居状态通常与当前状态相似,因此,其值与当前状态的值接近。
|
||||||
|
|
||||||
|
请注意,局部搜索算法的工作方式是考虑当前状态下的一个节点,然后将该节点移动到当前状态的一个邻节点处。这与极大极小算法不同,例如,在极大极小算法中,状态空间中的每一个状态都被递归地考虑。
|
||||||
|
|
||||||
## 爬山算法(Hill Climbing)
|
## 爬山算法(Hill Climbing)
|
||||||
|
|
||||||
- 爬山算法是局部搜索算法的一种类型。在这个算法中,邻居的状态与当前的状态进行比较,如果其中任何一个状态更好,我们就把当前的节点从当-的状态改为该邻居的状态。“好状态”的定义是由目标函数决定的,倾向于一个较高的值,或一个递减函数,倾向于一个较低的值。
|
爬山算法是局部搜索算法的一种类型。在这个算法中,邻居的状态与当前的状态进行比较,如果其中任何一个状态更好,我们就把当前的节点从当-的状态改为该邻居的状态。“好状态”的定义是由目标函数决定的,倾向于一个较高的值,或一个递减函数,倾向于一个较低的值。
|
||||||
|
|
||||||
- 一个爬山算法在伪代码中会有以下样子:
|
一个爬山算法在伪代码中会有以下样子:
|
||||||
|
|
||||||
```txt
|
```txt
|
||||||
function Hill-Climb(problem):
|
function Hill-Climb(problem):
|
||||||
@@ -38,44 +39,45 @@ function Hill-Climb(problem):
|
|||||||
current = neighbor
|
current = neighbor
|
||||||
```
|
```
|
||||||
|
|
||||||
- 在这个算法中,我们从一个当前状态开始。在一些问题中,我们会知道当前的状态是什么,而在其他问题中,我们将不得不从随机选择一个状态开始。然后,我们重复以下动作:我们评估邻居状态,选择一个具有最佳值的邻居状态。然后,我们将这个邻居状态的值与当前状态的值进行比较。如果邻居状态更好,我们将当前状态切换到邻居状态,然后重复这个过程。当我们将最佳邻居与当前状态进行比较,并且当前状态更好时,该过程就结束了。然后,我们返回当前状态。
|
在这个算法中,我们从一个当前状态开始。在一些问题中,我们会知道当前的状态是什么,而在其他问题中,我们将不得不从随机选择一个状态开始。然后,我们重复以下动作:我们评估邻居状态,选择一个具有最佳值的邻居状态。然后,我们将这个邻居状态的值与当前状态的值进行比较。如果邻居状态更好,我们将当前状态切换到邻居状态,然后重复这个过程。当我们将最佳邻居与当前状态进行比较,并且当前状态更好时,该过程就结束了。然后,我们返回当前状态。
|
||||||
|
|
||||||
- 使用爬山算法,我们可以开始改进我们在例子中分配给医院的位置。经过几次转换,我们得到了以下状态:
|
使用爬山算法,我们可以开始改进我们在例子中分配给医院的位置。经过几次转换,我们得到了以下状态:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 在这个状态下,成本是11,比初始状态的成本17有所提高。然而,这还不是最佳状态。例如,将左边的医院移到左上角的房子下面,会使成本达到9,比11好。然而,这个版本的爬山算法无法达到这个目标,因为所有的邻居状态都至少和当前状态的成本一样高。从这个意义上说,爬坡算法是短视的,它经常满足于比其他一些解决方案更好的解决方案,但不一定是所有可能的解决方案中最好的。
|
在这个状态下,成本是11,比初始状态的成本17有所提高。然而,这还不是最佳状态。例如,将左边的医院移到左上角的房子下面,会使成本达到9,比11好。然而,这个版本的爬山算法无法达到这个目标,因为所有的邻居状态都至少和当前状态的成本一样高。从这个意义上说,爬坡算法是短视的,它经常满足于比其他一些解决方案更好的解决方案,但不一定是所有可能的解决方案中最好的。
|
||||||
|
|
||||||
### 局部和全局最小值和最大值
|
### 局部和全局最小值和最大值
|
||||||
|
|
||||||
- 如上所述,爬山算法可能卡在局部最大值或最小值中。局部最大值是一个比其相邻状态有更高值的状态。而全局最大值是指在状态空间的所有状态中具有最高值的状态。
|
如上所述,爬山算法可能卡在局部最大值或最小值中。局部最大值是一个比其相邻状态有更高值的状态。而全局最大值是指在状态空间的所有状态中具有最高值的状态。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 相比之下,局部最小值是一个比其相邻状态的值更低的状态。与此相对,全局最小值是指在状态空间中所有状态中具有最低值的状态。
|
相比之下,局部最小值是一个比其相邻状态的值更低的状态。与此相对,全局最小值是指在状态空间中所有状态中具有最低值的状态。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 爬山算法的问题是,它们可能会在局部最小和最大中结束。一旦算法到达一个点,其邻居状态就目标函数而言,比当前状态更糟糕,算法就会停止。特殊类型的局部最大值和最小值包括平坦的局部最大值/最小值 __(flat local maximum/minimum)__,即多个数值相同的状态相邻,形成一个plateau,其邻居状态的数值更差;以及 __shoulder__ ,邻居状态既可以更好,也可以更差。从plateau的中间开始,算法将无法向任何方向推进。
|
爬山算法的问题是,它们可能会在局部最小和最大中结束。一旦算法到达一个点,其邻居状态就目标函数而言,比当前状态更糟糕,算法就会停止。特殊类型的局部最大值和最小值包括平坦的局部最大值/最小值 __(flat local maximum/minimum)__,即多个数值相同的状态相邻,形成一个plateau,其邻居状态的数值更差;以及 __shoulder__ ,邻居状态既可以更好,也可以更差。从plateau的中间开始,算法将无法向任何方向推进。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
### 爬山算法的变体
|
### 爬山算法的变体
|
||||||
|
|
||||||
- 由于爬山算法的局限性,人们想到了多种变体来克服卡在局部最小值和最大值的问题。该算法的所有变体的共同点是,无论采用何种策略,每一种变体都有可能陷入局部最小或最大,并且没有办法继续优化。下面的算法是这样表述的:数值越大越好,但它们也适用于成本函数,其目标是使成本最小化。
|
由于爬山算法的局限性,人们想到了多种变体来克服卡在局部最小值和最大值的问题。该算法的所有变体的共同点是,无论采用何种策略,每一种变体都有可能陷入局部最小或最大,并且没有办法继续优化。下面的算法是这样表述的:数值越大越好,但它们也适用于成本函数,其目标是使成本最小化。
|
||||||
- __Steepest-ascent__: 选择值最高的邻居状态。
|
|
||||||
- Stochastic: 从值较高的邻居状态中随机选择。这样做,我们选择去任何比我们的值更高的方向。
|
|
||||||
- __First-choice__: 选择第一个值较高的邻居状态。
|
|
||||||
- __Random-restart__: 进行多次爬山。每次都从一个随机状态开始。比较每次试验的最大值,并在这些最大值中选择一个。
|
|
||||||
- __Local Beam Search__: 选择值最高的k个邻居状态。这与大多数本地搜索算法不同,它使用多个节点进行搜索,而不是只有一个节点。
|
|
||||||
|
|
||||||
- 虽然局部搜索算法并不总是给出最好的解决方案,但在考虑所有可能的状态在计算上不可行的情况下,它们往往能给出足够好的解决方案。
|
- __Steepest-ascent__: 选择值最高的邻居状态。
|
||||||
|
- Stochastic: 从值较高的邻居状态中随机选择。这样做,我们选择去任何比我们的值更高的方向。
|
||||||
|
- __First-choice__: 选择第一个值较高的邻居状态。
|
||||||
|
- __Random-restart__: 进行多次爬山。每次都从一个随机状态开始。比较每次试验的最大值,并在这些最大值中选择一个。
|
||||||
|
- __Local Beam Search__: 选择值最高的k个邻居状态。这与大多数本地搜索算法不同,它使用多个节点进行搜索,而不是只有一个节点。
|
||||||
|
|
||||||
|
虽然局部搜索算法并不总是给出最好的解决方案,但在考虑所有可能的状态在计算上不可行的情况下,它们往往能给出足够好的解决方案。
|
||||||
|
|
||||||
## 模拟退火算法(Simulated Annealing)
|
## 模拟退火算法(Simulated Annealing)
|
||||||
|
|
||||||
- 尽管我们已经看到了可以改进爬山算法的变种,但它们都有一个共同的错误:一旦算法达到局部最大值,它就会停止运行。模拟退火算法允许算法在卡在局部最大值时"摆脱"自己。
|
尽管我们已经看到了可以改进爬山算法的变种,但它们都有一个共同的错误:一旦算法达到局部最大值,它就会停止运行。模拟退火算法允许算法在卡在局部最大值时"摆脱"自己。
|
||||||
|
|
||||||
- 退火是指加热金属并让其缓慢冷却的过程,其作用是使金属变硬。这被用来比喻模拟退火算法,该算法开始时温度较高,更有可能做出随机决定,随着温度的降低,它变得不太可能做出随机决定,变得更加"坚定"。这种机制允许算法将其状态改变为比当前状态更差的邻居状态,这就是它如何摆脱局部最大值的原因。以下是模拟退火法的伪代码:
|
退火是指加热金属并让其缓慢冷却的过程,其作用是使金属变硬。这被用来比喻模拟退火算法,该算法开始时温度较高,更有可能做出随机决定,随着温度的降低,它变得不太可能做出随机决定,变得更加"坚定"。这种机制允许算法将其状态改变为比当前状态更差的邻居状态,这就是它如何摆脱局部最大值的原因。以下是模拟退火法的伪代码:
|
||||||
|
|
||||||
```txt
|
```txt
|
||||||
function Simulated-Annealing(problem, max):
|
function Simulated-Annealing(problem, max):
|
||||||
@@ -90,35 +92,37 @@ function Simulated-Annealing(problem, max):
|
|||||||
return current
|
return current
|
||||||
```
|
```
|
||||||
|
|
||||||
- 该算法将一个`problem`和`max`作为输入,`max`是它应该重复的次数。对于每个迭代,`T`是用一个`Temperature`函数来设置的。这个函数在早期迭代中返回一个较高的值(当`t`较低时),在后期迭代中返回一个较低的值(当`t`较高时)。然后,随机选择一个邻居状态,并计算`ΔE`,使其量化邻居状态比当前状态好的程度。如果邻居状态比当前状态好(`ΔE>0`),像以前一样,我们将当前状态设置为邻居状态。然而,当邻居状态较差时(`ΔE<0`),我们仍然可能将我们的当前状态设置为该邻居状态,并且我们以$e^{ΔE/t}$的概率这样做。这里的意思是,更小的`ΔE`将导致邻居状态被选择的概率降低,而温度`t`越高,邻居状态被选择的概率越高。这意味着邻居状态越差,被选择的可能性就越小,而算法在其过程中越早,就越有可能将一个较差的邻居状态设置为当前状态。这背后的数学原理如下:`e`是一个常数(大约2.72),`ΔE`是负数(因为这个邻居比当前状态更糟糕)。温度`t`越高,ΔE/`t`就越接近于0,使概率更接近于1。
|
该算法将一个`problem`和`max`作为输入,`max`是它应该重复的次数。对于每个迭代,`T`是用一个`Temperature`函数来设置的。这个函数在早期迭代中返回一个较高的值(当`t`较低时),在后期迭代中返回一个较低的值(当`t`较高时)。然后,随机选择一个邻居状态,并计算`ΔE`,使其量化邻居状态比当前状态好的程度。如果邻居状态比当前状态好(`ΔE>0`),像以前一样,我们将当前状态设置为邻居状态。然而,当邻居状态较差时(`ΔE<0`),我们仍然可能将我们的当前状态设置为该邻居状态,并且我们以$e^{ΔE/t}$的概率这样做。这里的意思是,更小的`ΔE`将导致邻居状态被选择的概率降低,而温度`t`越高,邻居状态被选择的概率越高。这意味着邻居状态越差,被选择的可能性就越小,而算法在其过程中越早,就越有可能将一个较差的邻居状态设置为当前状态。这背后的数学原理如下:`e`是一个常数(大约2.72),`ΔE`是负数(因为这个邻居比当前状态更糟糕)。温度`t`越高,ΔE/`t`就越接近于0,使概率更接近于1。
|
||||||
|
|
||||||
### 旅行商问题(Traveling Salesman Problem)
|
### 旅行商问题(Traveling Salesman Problem)
|
||||||
|
|
||||||
- 在旅行商问题中,任务是连接所有的点,同时选择最短的距离。例如,这就是快递公司需要做的事情:找到从商店到所有客户家的最短路线,然后再返回。
|
在旅行商问题中,任务是连接所有的点,同时选择最短的距离。例如,这就是快递公司需要做的事情:找到从商店到所有客户家的最短路线,然后再返回。
|
||||||
|
|
||||||
| 优化前 | 优化后 |
|
| 优化前 | 优化后 |
|
||||||
| ------------------------------ | ------------------------------ |
|
| ------------------------------ | ------------------------------ |
|
||||||
|  |  |
|
|  |  |
|
||||||
|
|
||||||
- 在这种情况下,邻居状态可以被看作是两个箭头互换位置的状态。计算每一个可能的组合使得这个问题在计算上要求很高(10个点给了我们10!或者说3,628,800条可能的路线)。通过使用模拟退火算法,可以以较低的计算成本找到一个好的解决方案。
|
在这种情况下,邻居状态可以被看作是两个箭头互换位置的状态。计算每一个可能的组合使得这个问题在计算上要求很高(10个点给了我们10!或者说3,628,800条可能的路线)。通过使用模拟退火算法,可以以较低的计算成本找到一个好的解决方案。
|
||||||
|
|
||||||
## 线性规划(Linear Programming)
|
## 线性规划(Linear Programming)
|
||||||
|
|
||||||
- 线性规划是一个优化线性方程(y=ax₁+bx₂+...形式的方程)的问题系列。
|
线性规划是一个优化线性方程(y=ax₁+bx₂+...形式的方程)的问题系列。
|
||||||
|
|
||||||
- 线性规划有以下内容:
|
线性规划有以下内容:
|
||||||
- 一个我们想要最小化的成本函数:c₁x₁ + c₂x₂ + ... + cₙxₙ。这里,每个x是一个变量,它与一些成本c相关联。
|
|
||||||
- 一个约束条件,它表示为一个变量的总和,它要么小于或等于一个值(a₁x₁+a₂x₂+...+aₙxₙ≤b),要么正好等于这个值(a₁x₁+a₂x₂+...+aₙxₙ=b)。在这种情况下,x是一个变量,a是与之相关的一些资源,而b是我们可以为这个问题投入多少资源。
|
|
||||||
- 变量的域(例如,一个变量不能是负数),形式为lᵢ≤xᵢ≤uᵢ。
|
|
||||||
|
|
||||||
- 请考虑以下例子:
|
- 一个我们想要最小化的成本函数:c₁x₁ + c₂x₂ + ... + cₙxₙ。这里,每个x是一个变量,它与一些成本c相关联。
|
||||||
- 两台机器,X₁和X₂。X₁的运行成本为50美元/小时,X₂的运行成本为80美元/小时。我们的目标是使成本最小化。这可以被表述为一个成本函数:50x₁+80x₂。
|
- 一个约束条件,它表示为一个变量的总和,它要么小于或等于一个值(a₁x₁+a₂x₂+...+aₙxₙ≤b),要么正好等于这个值(a₁x₁+a₂x₂+...+aₙxₙ=b)。在这种情况下,x是一个变量,a是与之相关的一些资源,而b是我们可以为这个问题投入多少资源。
|
||||||
- X₁每小时需要5个单位的劳动力。X₂每小时需要2个单位的劳动力。总共需要花费20个单位的劳动力。这可以被形式化为一个约束条件:5x₁ + 2x₂ ≤ 20。
|
- 变量的域(例如,一个变量不能是负数),形式为lᵢ≤xᵢ≤uᵢ。
|
||||||
- X₁每小时生产10个单位的产品。X₂每小时生产12个单位的产品。公司需要90个单位的产出。这是另一个约束条件。从字面上看,它可以被改写为10x₁+12x₂≥90。然而,约束条件必须是(a₁x₁+a₂x₂+...+aₙxₙ≤b)或(a₁x₁+a₂x₂+...+aₙxₙ=b)。因此,我们乘以(-1),得到一个所需形式的等价方程:(-10x₁)+(-12x₂)≤-90。
|
|
||||||
|
|
||||||
- 线性规划的优化算法需要几何学和线性代数的背景知识,而我们并不想假设这些知识。相反,我们可以使用已经存在的算法,如Simplex和Interior-Point。
|
请考虑以下例子:
|
||||||
|
|
||||||
- 下面是一个使用Python中scipy库的线性规划例子:
|
- 两台机器,X₁和X₂。X₁的运行成本为50美元/小时,X₂的运行成本为80美元/小时。我们的目标是使成本最小化。这可以被表述为一个成本函数:50x₁+80x₂。
|
||||||
|
- X₁每小时需要5个单位的劳动力。X₂每小时需要2个单位的劳动力。总共需要花费20个单位的劳动力。这可以被形式化为一个约束条件:5x₁ + 2x₂ ≤ 20。
|
||||||
|
- X₁每小时生产10个单位的产品。X₂每小时生产12个单位的产品。公司需要90个单位的产出。这是另一个约束条件。从字面上看,它可以被改写为10x₁+12x₂≥90。然而,约束条件必须是(a₁x₁+a₂x₂+...+aₙxₙ≤b)或(a₁x₁+a₂x₂+...+aₙxₙ=b)。因此,我们乘以(-1),得到一个所需形式的等价方程:(-10x₁)+(-12x₂)≤-90。
|
||||||
|
|
||||||
|
线性规划的优化算法需要几何学和线性代数的背景知识,而我们并不想假设这些知识。相反,我们可以使用已经存在的算法,如Simplex和Interior-Point。
|
||||||
|
|
||||||
|
下面是一个使用Python中scipy库的线性规划例子:
|
||||||
|
|
||||||
```python
|
```python
|
||||||
import scipy.optimize
|
import scipy.optimize
|
||||||
@@ -139,41 +143,44 @@ else:
|
|||||||
|
|
||||||
## 约束满足(Constraint Satisfaction)
|
## 约束满足(Constraint Satisfaction)
|
||||||
|
|
||||||
- 约束满足问题是一类需要在满足某些条件下为变量赋值的问题。
|
约束满足问题是一类需要在满足某些条件下为变量赋值的问题。
|
||||||
|
|
||||||
- 约束条件满足问题具有以下特性:
|
约束条件满足问题具有以下特性:
|
||||||
- 变量集合{x₁,x₂,...,xₙ}。
|
|
||||||
- 每个变量域的集合{D₁, D₂, ..., Dₙ}。
|
- 变量集合{x₁,x₂,...,xₙ}。
|
||||||
- 一组约束条件C
|
- 每个变量域的集合{D₁, D₂, ..., Dₙ}。
|
||||||
|
- 一组约束条件C
|
||||||
|
|
||||||
|
数独可以表示为一个约束满足问题,每个空方块是一个变量,域是数字1-9,而约束是不能彼此相等的方块。
|
||||||
|
|
||||||
- 数独可以表示为一个约束满足问题,每个空方块是一个变量,域是数字1-9,而约束是不能彼此相等的方块。
|
|
||||||

|

|
||||||
|
|
||||||
- 再考虑一个例子。每个学生1-4都在选修A、B、...、G中的三门课程。每门课程都需要有考试,可能的考试日是星期一、星期二和星期三。但是,同一个学生不能在同一天有两次考试。在这种情况下,变量是课程,域是天数,约束条件是哪些课程不能在同一天安排考试,因为是同一个学生在考试。这可以直观地显示如下:
|
再考虑一个例子。每个学生1-4都在选修A、B、...、G中的三门课程。每门课程都需要有考试,可能的考试日是星期一、星期二和星期三。但是,同一个学生不能在同一天有两次考试。在这种情况下,变量是课程,域是天数,约束条件是哪些课程不能在同一天安排考试,因为是同一个学生在考试。这可以直观地显示如下:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 这个问题可以用约束条件来解决,约束条件用图来表示。图中的每个节点是一门课程,如果两门课程不能安排在同一天,则在它们之间画一条边。在这种情况下,该图看起来是这样的:
|
这个问题可以用约束条件来解决,约束条件用图来表示。图中的每个节点是一门课程,如果两门课程不能安排在同一天,则在它们之间画一条边。在这种情况下,该图看起来是这样的:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 关于约束满足问题,还有几个值得了解的术语:
|
关于约束满足问题,还有几个值得了解的术语:
|
||||||
- 硬约束(Hard Constraint)是指在一个正确的解决方案中必须满足的约束。
|
|
||||||
- 软约束(Soft Constraint)是一种约束,表示哪种解决方案比其他解决方案更受欢迎。
|
- 硬约束(Hard Constraint)是指在一个正确的解决方案中必须满足的约束。
|
||||||
- 一元约束(Unary Constraint)是指只涉及一个变量的约束。在我们的例子中,一元约束是指课程A在周一不能有考试{A≠周一}。
|
- 软约束(Soft Constraint)是一种约束,表示哪种解决方案比其他解决方案更受欢迎。
|
||||||
- 二元约束(Binary Constraint)是一种涉及两个变量的约束。这就是我们在上面的例子中使用的约束类型,表示两个课程不能有相同的值{A ≠ B}。
|
- 一元约束(Unary Constraint)是指只涉及一个变量的约束。在我们的例子中,一元约束是指课程A在周一不能有考试{A≠周一}。
|
||||||
|
- 二元约束(Binary Constraint)是一种涉及两个变量的约束。这就是我们在上面的例子中使用的约束类型,表示两个课程不能有相同的值{A ≠ B}。
|
||||||
|
|
||||||
### 节点一致性(Node Consistency)
|
### 节点一致性(Node Consistency)
|
||||||
|
|
||||||
- 节点一致性是指一个变量域中的所有值都满足该变量的一元约束。
|
节点一致性是指一个变量域中的所有值都满足该变量的一元约束。
|
||||||
|
|
||||||
- 例如,让我们拿两门课程,A和B。每门课程的域是{Monday, Tuesday, Wednesday},约束条件是{A≠Mon,B≠Tue,B≠Mon,A≠B}。现在,A和B都不是一致的,因为现有的约束条件使它们不能取其域中的每一个值。然而,如果我们从A的域中移除Monday,那么它就会有节点一致性。为了实现B的节点一致性,我们必须从它的域中删除Monday和Tuesday。
|
例如,让我们拿两门课程,A和B。每门课程的域是{Monday, Tuesday, Wednesday},约束条件是{A≠Mon,B≠Tue,B≠Mon,A≠B}。现在,A和B都不是一致的,因为现有的约束条件使它们不能取其域中的每一个值。然而,如果我们从A的域中移除Monday,那么它就会有节点一致性。为了实现B的节点一致性,我们必须从它的域中删除Monday和Tuesday。
|
||||||
|
|
||||||
### 弧一致性(Arc Consistency)
|
### 弧一致性(Arc Consistency)
|
||||||
|
|
||||||
- 弧一致性是指一个变量域中的所有值都满足该变量的二元约束(注意,我们现在用"弧"来指代我们以前所说的 "边")。换句话说,要使X对Y具有弧一致性,就要从X的域中移除元素,直到X的每个选择都有Y的可能选择。
|
弧一致性是指一个变量域中的所有值都满足该变量的二元约束(注意,我们现在用"弧"来指代我们以前所说的 "边")。换句话说,要使X对Y具有弧一致性,就要从X的域中移除元素,直到X的每个选择都有Y的可能选择。
|
||||||
|
|
||||||
- 考虑到我们之前的例子,修改后的域:A:{Tuesday, Wednesday}和B:{Wednesday}。如果A与B是弧一致的,那么无论A的考试被安排在哪一天(从它的域来看),B仍然能够安排考试。A与B是弧一致的吗?如果A取值为Tuesday,那么B可以取值为Wednesday。然而,如果A取值为Wednesday,那么就没有B可以取的值(记住,其中一个约束是A≠B)。因此,A与B不是弧一致的。为了改变这种情况,我们可以从A的域中删除Wednesday。然后,A的任何取值(Tuesday是唯一的选择)都会给B留下一个取值(Wednesday)。现在,A与B是弧一致的。让我们看看一个伪代码的算法,使一个变量相对于其他变量是弧一致的(注意,csp代表 "约束满足问题")。
|
考虑到我们之前的例子,修改后的域:A:{Tuesday, Wednesday}和B:{Wednesday}。如果A与B是弧一致的,那么无论A的考试被安排在哪一天(从它的域来看),B仍然能够安排考试。A与B是弧一致的吗?如果A取值为Tuesday,那么B可以取值为Wednesday。然而,如果A取值为Wednesday,那么就没有B可以取的值(记住,其中一个约束是A≠B)。因此,A与B不是弧一致的。为了改变这种情况,我们可以从A的域中删除Wednesday。然后,A的任何取值(Tuesday是唯一的选择)都会给B留下一个取值(Wednesday)。现在,A与B是弧一致的。让我们看看一个伪代码的算法,使一个变量相对于其他变量是弧一致的(注意,csp代表 "约束满足问题")。
|
||||||
|
|
||||||
```python
|
```python
|
||||||
function Revise(csp, X, Y):
|
function Revise(csp, X, Y):
|
||||||
@@ -185,9 +192,9 @@ function Revise(csp, X, Y):
|
|||||||
return revised
|
return revised
|
||||||
```
|
```
|
||||||
|
|
||||||
- 这个算法从跟踪X的域是否有任何变化开始,使用变量revised,这在我们研究的下一个算法中会很有用。然后,代码对X的域中的每一个值进行重复,看看Y是否有一个满足约束条件的值。如果是,则什么都不做,如果不是,则从X的域中删除这个值。
|
这个算法从跟踪X的域是否有任何变化开始,使用变量revised,这在我们研究的下一个算法中会很有用。然后,代码对X的域中的每一个值进行重复,看看Y是否有一个满足约束条件的值。如果是,则什么都不做,如果不是,则从X的域中删除这个值。
|
||||||
|
|
||||||
- 通常情况下,我们感兴趣的是使整个问题的弧一致,而不仅仅是一个变量相对于另一个变量的一致性。在这种情况下,我们将使用一种叫做AC-3的算法,该算法使用Revise:
|
通常情况下,我们感兴趣的是使整个问题的弧一致,而不仅仅是一个变量相对于另一个变量的一致性。在这种情况下,我们将使用一种叫做AC-3的算法,该算法使用Revise:
|
||||||
|
|
||||||
```python
|
```python
|
||||||
function AC-3(csp):
|
function AC-3(csp):
|
||||||
@@ -202,22 +209,23 @@ function AC-3(csp):
|
|||||||
return true
|
return true
|
||||||
```
|
```
|
||||||
|
|
||||||
- 该算法将问题中的所有弧添加到一个队列中。每当它考虑一个弧时,它就把它从队列中删除。然后,它运行Revise算法,看这个弧是否一致。如果做了修改使其一致,则需要进一步的行动。如果得到的X的域是空的,这意味着这个约束满足问题是无法解决的(因为没有任何X可以取的值会让Y在约束条件下取任何值)。如果问题在上一步中没有被认为是不可解决的,那么,由于X的域被改变了,我们需要看看与X相关的所有弧是否仍然一致。也就是说,我们把除了Y以外的所有X的邻居,把他们和X之间的弧添加到队列中。然而,如果Revise算法返回false,意味着域没有被改变,我们只需继续考虑其他弧。
|
该算法将问题中的所有弧添加到一个队列中。每当它考虑一个弧时,它就把它从队列中删除。然后,它运行Revise算法,看这个弧是否一致。如果做了修改使其一致,则需要进一步的行动。如果得到的X的域是空的,这意味着这个约束满足问题是无法解决的(因为没有任何X可以取的值会让Y在约束条件下取任何值)。如果问题在上一步中没有被认为是不可解决的,那么,由于X的域被改变了,我们需要看看与X相关的所有弧是否仍然一致。也就是说,我们把除了Y以外的所有X的邻居,把他们和X之间的弧添加到队列中。然而,如果Revise算法返回false,意味着域没有被改变,我们只需继续考虑其他弧。
|
||||||
|
|
||||||
- 虽然弧一致性的算法可以简化问题,但不一定能解决问题,因为它只考虑了二元约束,而没有考虑多个节点可能的相互连接方式。我们之前的例子中,4个学生中的每个人都在选修3门课程,对其运行AC-3后,仍然没有变化。
|
虽然弧一致性的算法可以简化问题,但不一定能解决问题,因为它只考虑了二元约束,而没有考虑多个节点可能的相互连接方式。我们之前的例子中,4个学生中的每个人都在选修3门课程,对其运行AC-3后,仍然没有变化。
|
||||||
|
|
||||||
- 我们讲过[搜索](4.3.1搜索.md)问题。一个约束满足问题可以被看作是一个搜索问题:
|
我们讲过[搜索](4.3.1搜索.md)问题。一个约束满足问题可以被看作是一个搜索问题:
|
||||||
- 初始状态(Initial state):空赋值(所有变量都没有分配任何数值)。
|
|
||||||
- 动作(Action):在赋值中加入一个{变量=值};也就是说,给某个变量一个值。
|
|
||||||
- 过渡模型(Transition model):显示添加赋值如何改变变量。这没有什么深度:过渡模型返回包括最新动作后的赋值的状态。
|
|
||||||
- 目标测试(Goal test):检查所有变量是否被赋值,所有约束条件是否得到满足。
|
|
||||||
- 路径成本函数(Path cost function):所有路径的成本都是一样的。正如我们前面提到的,与典型的搜索问题相比,优化问题关心的是解决方案,而不是通往解决方案的路线。
|
|
||||||
|
|
||||||
- 然而,把约束满足问题作为一个普通的搜索问题来处理,是非常低效的。相反,我们可以利用约束满足问题的结构来更有效地解决它。
|
- 初始状态(Initial state):空赋值(所有变量都没有分配任何数值)。
|
||||||
|
- 动作(Action):在赋值中加入一个{变量=值};也就是说,给某个变量一个值。
|
||||||
|
- 过渡模型(Transition model):显示添加赋值如何改变变量。这没有什么深度:过渡模型返回包括最新动作后的赋值的状态。
|
||||||
|
- 目标测试(Goal test):检查所有变量是否被赋值,所有约束条件是否得到满足。
|
||||||
|
- 路径成本函数(Path cost function):所有路径的成本都是一样的。正如我们前面提到的,与典型的搜索问题相比,优化问题关心的是解决方案,而不是通往解决方案的路线。
|
||||||
|
|
||||||
|
然而,把约束满足问题作为一个普通的搜索问题来处理,是非常低效的。相反,我们可以利用约束满足问题的结构来更有效地解决它。
|
||||||
|
|
||||||
### 回溯搜索(Backtracking Search)
|
### 回溯搜索(Backtracking Search)
|
||||||
|
|
||||||
- 回溯搜索是一种考虑约束满足搜索问题结构的搜索算法。一般来说,它是一个递归函数,只要值满足约束,它就会尝试继续赋值。如果违反了约束,它将尝试不同的赋值。让我们看看它的伪代码:
|
回溯搜索是一种考虑约束满足搜索问题结构的搜索算法。一般来说,它是一个递归函数,只要值满足约束,它就会尝试继续赋值。如果违反了约束,它将尝试不同的赋值。让我们看看它的伪代码:
|
||||||
|
|
||||||
```python
|
```python
|
||||||
function Backtrack(assignment, csp):
|
function Backtrack(assignment, csp):
|
||||||
@@ -234,19 +242,19 @@ function Backtrack(assignment, csp):
|
|||||||
return failure
|
return failure
|
||||||
```
|
```
|
||||||
|
|
||||||
- 换句话说,如果当前赋值完成,则该算法返回当前赋值。这意味着,如果完成了算法,它将不会执行任何额外的操作,它只会返回已成立的赋值。如果赋值不完整,算法会选择任何尚未赋值的变量。然后,算法尝试为变量赋值,并对结果赋值再次运行回溯算法(递归)。然后,它检查结果值。如果不是失败,则表示赋值已完成,并且应返回此赋值。如果结果值失败,则删除最近的赋值,并尝试新的可能值,重复相同的过程。如果域中所有可能的值都返回失败,这意味着我们需要回溯。也就是说,问题出在之前的一些作业上。如果这种情况发生在我们开始使用的变量上,那么这意味着没有解决方案满足约束。
|
换句话说,如果当前赋值完成,则该算法返回当前赋值。这意味着,如果完成了算法,它将不会执行任何额外的操作,它只会返回已成立的赋值。如果赋值不完整,算法会选择任何尚未赋值的变量。然后,算法尝试为变量赋值,并对结果赋值再次运行回溯算法(递归)。然后,它检查结果值。如果不是失败,则表示赋值已完成,并且应返回此赋值。如果结果值失败,则删除最近的赋值,并尝试新的可能值,重复相同的过程。如果域中所有可能的值都返回失败,这意味着我们需要回溯。也就是说,问题出在之前的一些作业上。如果这种情况发生在我们开始使用的变量上,那么这意味着没有解决方案满足约束。
|
||||||
|
|
||||||
- 考虑以下行动方案:
|
考虑以下行动方案:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 我们从空赋值开始。然后,我们选择变量A,并给它赋值`Mon`。然后,使用这个赋值,我们再次运行算法。既然A已经有了一个赋值,算法将考虑B,并将`Mon`赋值给它。此赋值返回`false`,因此算法将尝试在`Tue`为B赋值,而不是在给定上一个赋值的情况下为C赋值。这个新的赋值满足约束条件,在给定这个赋值的情况下,下一步将考虑一个新的变量。例如,如果将`Tue`或`Wed`也赋值给B会导致失败,那么算法将回溯并返回到考虑A,为其分配另一个值,即`Tue`。如果`Tue`和`Wed`也失败了,那么这意味着我们已经尝试了所有可能的赋值,该问题是无法解决的。
|
我们从空赋值开始。然后,我们选择变量A,并给它赋值`Mon`。然后,使用这个赋值,我们再次运行算法。既然A已经有了一个赋值,算法将考虑B,并将`Mon`赋值给它。此赋值返回`false`,因此算法将尝试在`Tue`为B赋值,而不是在给定上一个赋值的情况下为C赋值。这个新的赋值满足约束条件,在给定这个赋值的情况下,下一步将考虑一个新的变量。例如,如果将`Tue`或`Wed`也赋值给B会导致失败,那么算法将回溯并返回到考虑A,为其分配另一个值,即`Tue`。如果`Tue`和`Wed`也失败了,那么这意味着我们已经尝试了所有可能的赋值,该问题是无法解决的。
|
||||||
|
|
||||||
- 在源代码部分,您可以从头开始实现的回溯算法。然而,这种算法被广泛使用,因此,多个库已经包含了它的实现。
|
在源代码部分,您可以从头开始实现的回溯算法。然而,这种算法被广泛使用,因此,多个库已经包含了它的实现。
|
||||||
|
|
||||||
## 推理(Inference)
|
## 推理(Inference)
|
||||||
|
|
||||||
- 尽管回溯搜索比简单搜索更有效,但它仍然需要大量的算力。另一方面,满足弧一致性需要的算力较低。通过将回溯搜索与推理交织在一起(满足弧一致性),我们可以得到一种更有效的算法。该算法被称为“保持弧一致性” __(Maintaining Arc-Consistency)__ 算法。该算法将在每次新的回溯搜索分配之后满足弧一致性。具体来说,在我们对X进行新的赋值后,我们将调用`AC-3`算法,并从所有弧(Y,X)的队列开始,其中Y是X的邻居(而不是问题中所有弧的队列)。以下是一个经过修订的Backtrack算法,该算法保持了弧的一致性。
|
尽管回溯搜索比简单搜索更有效,但它仍然需要大量的算力。另一方面,满足弧一致性需要的算力较低。通过将回溯搜索与推理交织在一起(满足弧一致性),我们可以得到一种更有效的算法。该算法被称为“保持弧一致性” __(Maintaining Arc-Consistency)__ 算法。该算法将在每次新的回溯搜索分配之后满足弧一致性。具体来说,在我们对X进行新的赋值后,我们将调用`AC-3`算法,并从所有弧(Y,X)的队列开始,其中Y是X的邻居(而不是问题中所有弧的队列)。以下是一个经过修订的Backtrack算法,该算法保持了弧的一致性。
|
||||||
|
|
||||||
```python
|
```python
|
||||||
function Backtrack(assignment, csp):
|
function Backtrack(assignment, csp):
|
||||||
@@ -266,28 +274,28 @@ function Backtrack(assignment, csp):
|
|||||||
return failure
|
return failure
|
||||||
```
|
```
|
||||||
|
|
||||||
- Inference函数运行AC-3算法,如前所述。它的输出是通过满足弧一致性可以做出的所有推断。从字面上看,这些是可以从以前的赋值和约束满足问题的结构中推导出来的新赋值。
|
Inference函数运行AC-3算法,如前所述。它的输出是通过满足弧一致性可以做出的所有推断。从字面上看,这些是可以从以前的赋值和约束满足问题的结构中推导出来的新赋值。
|
||||||
|
|
||||||
- 还有其他方法可以提高算法的效率。到目前为止,我们随机选择了一个未分配的变量。然而,有些选择比其他选择更有可能更快地找到解决方案。这需要使用启发式方法。启发式是一条经验法则,这意味着,通常情况下,它会比遵循随机的方法带来更好的结果,但不能保证总是更优。
|
还有其他方法可以提高算法的效率。到目前为止,我们随机选择了一个未分配的变量。然而,有些选择比其他选择更有可能更快地找到解决方案。这需要使用启发式方法。启发式是一条经验法则,这意味着,通常情况下,它会比遵循随机的方法带来更好的结果,但不能保证总是更优。
|
||||||
|
|
||||||
- __最小剩余值(Minimum Remaining Values(MRV))__ 就是这样一种启发式方法。这里的想法是,如果一个变量的域被推理限制了,现在它只剩下一个值(甚至是两个值),那么通过进行这种赋值,我们将减少以后可能需要进行的回溯次数。也就是说,我们迟早要做这个赋值,因为它是从满足弧一致性中推断出来的。如果这项任务失败了,最好尽快发现,避免以后的回溯。
|
__最小剩余值(Minimum Remaining Values(MRV))__ 就是这样一种启发式方法。这里的想法是,如果一个变量的域被推理限制了,现在它只剩下一个值(甚至是两个值),那么通过进行这种赋值,我们将减少以后可能需要进行的回溯次数。也就是说,我们迟早要做这个赋值,因为它是从满足弧一致性中推断出来的。如果这项任务失败了,最好尽快发现,避免以后的回溯。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 例如,在给定当前赋值的情况下缩小变量的域后,使用MRV启发式,我们接下来将选择变量C,并以Wed为其赋值。
|
例如,在给定当前赋值的情况下缩小变量的域后,使用MRV启发式,我们接下来将选择变量C,并以Wed为其赋值。
|
||||||
|
|
||||||
- __度(Degree)__ 启发式依赖于变量的度,其中度是指将一个变量连接到其他变量的弧数。通过一次赋值选择度最高的变量,我们约束了多个其他变量,从而加快了算法的进程。
|
__度(Degree)__ 启发式依赖于变量的度,其中度是指将一个变量连接到其他变量的弧数。通过一次赋值选择度最高的变量,我们约束了多个其他变量,从而加快了算法的进程。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 例如,上面所有的变量都有相同大小的域。因此,我们应该选择一个度最高的域,它将是变量E。
|
例如,上面所有的变量都有相同大小的域。因此,我们应该选择一个度最高的域,它将是变量E。
|
||||||
|
|
||||||
- 这两种启发式方法并不总是适用的。例如,当多个变量在其域中具有相同的最小值时,或者当多个变数具有相同的最高度时。
|
这两种启发式方法并不总是适用的。例如,当多个变量在其域中具有相同的最小值时,或者当多个变数具有相同的最高度时。
|
||||||
|
|
||||||
- 另一种提高算法效率的方法是,当我们从变量的域中选择一个值时,使用另一种启发式方法。在这里,我们使用 __最小约束值(Least Constraining Values)__ 启发式,在这里我们选择将约束最少其他变量的值。这里的想法是,在度启发式中,我们希望使用更可能约束其他变量的变量,而在这里,我们希望这个变量对其他变量的约束最少。也就是说,我们希望找到可能是最大潜在麻烦源的变量(度最高的变量),然后使其尽可能不麻烦(为其赋值约束其他变量最少的值)。
|
另一种提高算法效率的方法是,当我们从变量的域中选择一个值时,使用另一种启发式方法。在这里,我们使用 __最小约束值(Least Constraining Values)__ 启发式,在这里我们选择将约束最少其他变量的值。这里的想法是,在度启发式中,我们希望使用更可能约束其他变量的变量,而在这里,我们希望这个变量对其他变量的约束最少。也就是说,我们希望找到可能是最大潜在麻烦源的变量(度最高的变量),然后使其尽可能不麻烦(为其赋值约束其他变量最少的值)。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
- 例如,让我们考虑变量C。如果我们将`Tue`分配给它,我们将对所有B、E和F施加约束。然而,如果我们选择`Wed`,我们将只对B和E施加约束。因此,选择`Tue`可能更好。
|
例如,让我们考虑变量C。如果我们将`Tue`分配给它,我们将对所有B、E和F施加约束。然而,如果我们选择`Wed`,我们将只对B和E施加约束。因此,选择`Tue`可能更好。
|
||||||
|
|
||||||
- 总之,优化问题可以用多种方式来表述。在这,我们考虑了局部搜索、线性规划和约束满足。
|
总之,优化问题可以用多种方式来表述。在这,我们考虑了局部搜索、线性规划和约束满足。
|
||||||
|
|||||||
Reference in New Issue
Block a user