fix: 目录调整
This commit is contained in:
337
8.基础学科/8.1经济学科普Part1.md
Normal file
337
8.基础学科/8.1经济学科普Part1.md
Normal file
@@ -0,0 +1,337 @@
|
||||
# 经济学科普#Part1
|
||||
|
||||
Author:ou_3840181b7c52ab34d2aa31f288fc7bc3
|
||||
|
||||
# 前言
|
||||
|
||||
经济学,研究的是人类经济活动的规律。
|
||||
|
||||
现实生活的经济现象互相冗杂在一起,作为一个初学者,我们很难很难单独抽出来进行分析。
|
||||
|
||||
为了简化问题,方便思考,我们在下文建立一个最简单的生产模型,在一个完全封闭的村庄内,有人能生产小麦,有人能用小麦做出面包,人最终消费的是面包。通过探究这样一个最基本的二元生产关系模型,我们可以得到一些初步的经济学结论。这对于进一步的学习、思考有着举足轻重的作用。
|
||||
|
||||
另外,我们虽然基于这个及其建议的模型开始讨论,但模型稍作改动就可以用于考察更复杂的经济问题,例如,我们可以引入铸币部门,发放货币,进而考察铸币税的影响,我们可以引入另一个村庄,只具备生产衣物的能力,由此来考察两个经济体之间的外贸,我们还可以假设小麦加工厂由 N 个小型加工厂组成,考察加工厂之间的关系...上面只是举了一些例子,实际上别的思考方式还有很多。
|
||||
|
||||
这篇文档只会介绍简单的经济学概念和模型,希望能够引起一些思考。更深入的内容,如结合实际、结合金融工程的内容,会在之后另有讨论。
|
||||
|
||||
# 最简单生产-消费模型
|
||||
|
||||
## 以物换物和它的缺陷
|
||||
|
||||
我们先从构建一个最最简单的基本模型开始。
|
||||
|
||||
考虑一个村落有 2 个人,一个人能制造面粉,另一个人能制作面包,因为一些原因(精力不足),他们不能交叉彼此的分工
|
||||
|
||||
这样一来,做面粉的如果吃不到面包就会饿死,做面包的拿不到面粉也会饿死,如果这两人不能通过某种机制来调配彼此的资源,这两人都是死路一条
|
||||
|
||||
这两人接下来会通过某种方式来调配资源:
|
||||
|
||||
最简单的方式是,以物换物
|
||||
|
||||
用面粉来换面包
|
||||
|
||||
这样两个人都饿不死了
|
||||
|
||||
但这样也存在一些局限性,如果有一年严重欠收,面包都吃完了,面粉刚做出来,因为没有面包,交易无法发生,那两个人就又都饿死了
|
||||
|
||||
也就是说,上面这种交易方式,虽然本质(以物换物,进行资源的调配是经济的本质),但不够灵活。
|
||||
|
||||
那么怎么才能灵活呢?
|
||||
|
||||
## 信用、货币的引入
|
||||
|
||||
引入一个概念,<strong>信用</strong>。
|
||||
|
||||
做面粉和做面包的都彼此信任,相信对面总有一天会兑现承诺,允许赊账
|
||||
|
||||
> 需要注意的是,这里引入了灵活,事实上就引入了风险。在后面的讨论中会反复看到,引入灵活就是引入风险,但灵活的诱惑太大,我们不得不接受风险。灵活从根本上带来了与实际生产脱钩的架空“财富”,这种“财富”可以推进生产力的发展,但过度膨胀的预期,形成了泡沫和经济周期。
|
||||
|
||||
那么,交易的过程可以这么表示了:
|
||||
|
||||
1. 做面包的问做面粉的要了 50 斤面粉
|
||||
2. 做面包的做出了 50 个面包,自己消费 25 个
|
||||
3. 做面包的给做面粉的 25 个面包
|
||||
|
||||
如果我们引入一种叫做“信用”的东西,这个交易过程可以用表画出来
|
||||
|
||||
| 行为 | 做面粉的 | 做面包的 |
|
||||
| -------- | --------------------------- | --------------------------- |
|
||||
| 开始 | 初始信用 0 | 初始信用 1 |
|
||||
| 交易面粉 | 信用 +1(1) | 信用-1(0),获得 50 斤面粉 |
|
||||
| 交易面包 | 信用-1(0),获得 25 个面包 | 信用 +1(1) |
|
||||
| 期末信用 | 0 | 1 |
|
||||
|
||||
稍微看一下就会发现,这个所谓的信用,和现在的<strong>货币</strong>没有任何区别,如果用现在的话说,一个信用就相当于 25 个面包
|
||||
|
||||
因此,可以得到一个结论,<strong>货币就是信用</strong>, 只是现在我们在使用货币时,信任的不是对面的人,而是国家,<strong>货币事实上就是国家信用</strong>。
|
||||
|
||||
> 这个加入第三方解决问题的思想在计算机科学里也非常常见(没有什么问题是加一个中间层不能解决的),在经济学里亦是如此。但额外补充,引入第三方信用的方案看似是分散了风险,但当考虑金融资产之间的关联性时,可能已经分散的风险又会集中,这是系统性风险的最大来源。(比如,国家如果破产了怎么办?)对应到对第三方的信用丧失,最常见的应对策略是买入避险资产,目前唯一的公认避险资产是黄金。(黄金从性质上来说具有天然的信用(不可人工制造,也就是不会突然增加减少,自然保有量即是信用),而且没有货币作用之外的属性(不能吃,不能穿,没有用,不是工业原料),是天然的货币)
|
||||
|
||||
至此,我们构建出了一个两个人间的简单闭环市场,当然,这里面有非常多非常理想的假设,例如人们都不会囤积面包,也不会有新的需求,也不会突然死亡
|
||||
|
||||
接下来,我们稍微展开一下,来玩一玩上面这个最简单的模型
|
||||
|
||||
## 价格对分配结果的影响
|
||||
|
||||
上面的情况中,我们始终在讨论一种可以周而复始,永远循环的情况。<strong>财富也不会增长或者减少</strong>。出现这种情况的根本原因是每次期初各方的货币总是等于期末各方的货币。换言之,如果每期中,有一方的货币总是减少一点,那么我们就无法建立一个可以永远循环下去的经济系统了。下面用表来举个例子。
|
||||
|
||||
面包价格:4 元/个,其他条件不变
|
||||
|
||||
| 行为 | 做面粉的 | 做面包的 |
|
||||
| -------- | ------------------------------ | ---------------- |
|
||||
| 开始 | 初始货币 100 | 初始货币 100 |
|
||||
| 交易面粉 | 货币 +50(150) | 获得 50 斤面粉 |
|
||||
| 交易面包 | 货币-100(50),获得 25 个面包 | 货币 +100(150) |
|
||||
| 期末 | 50(25 个面包) | 150(25 个面包) |
|
||||
|
||||
可以看到,由于价格比例的变动,为了维持原先的消费状况,面粉厂不得不增加相应的开支,再 1 轮交易之后,面粉厂就会因为没有货币而无法参与交易。
|
||||
|
||||
因此,在不均衡的价格体系中,<strong>假设没有外部货币补充,处于弱势的部门只能通过削减消费来维持经济系统的运转</strong>。而且,不难想到,<strong>即使有外部的货币补充,货币补充通常也难以直接送到弱势方</strong>,这反而会造成弱势方在分配面包时处于更加弱势的地位,不得不消费更少的面包。这可能是今天经常说的“剥削”。
|
||||
|
||||
这里还可以深入讨论一下,我们可以讨论一下价格比例的变动进而产生的分配变动。
|
||||
|
||||
我们考虑面粉价格与面包价格的比值,令其为 k
|
||||
|
||||
在之前我们的例子中,面粉价格与面包价格的比值恒为 0.5
|
||||
|
||||
现在我们考虑另 k=0.25,也就是上面的例子了,可以看到面粉厂若要保持货币不变少,只能消费 12.5 个面包,而面包厂可以消费 37.5 个面包。
|
||||
|
||||
更一般地,可以说,面粉厂消费的面包比例为 k,而面包厂消费的面包比例为 1-k。
|
||||
|
||||
<strong>也就是说,价格的绝对值并不怎么重要,重要的是价格之间的比值,这种价格比值的差异形成了分配的阶级性。</strong>
|
||||
|
||||
> 我们可以尝试着换一个角度来思考这个问题,从上述讨论中可以思考怎么样的价格调控是合理的,怎么样的是不合理的,通常来说,一些从直觉上感觉非常公平的定价方式,例如在成本基础上统一加一定量的利润,实际上是最不合理的,会带来非常严重的分配问题。
|
||||
|
||||
## 额外的收入
|
||||
|
||||
从之前的讨论中不难发现,要想获得储蓄的增长,唯一的方法是减少自己的消费,而且还需要另一方也同意增加自己的消费,两个条件均成立时储蓄才有望增长。
|
||||
|
||||
现在我们考虑一些最简单的情况,来考察储蓄对模型的影响,假设面粉厂和面包厂都有一份额外的工作可以带来货币,比如挖金矿。
|
||||
|
||||
黄金不可穿、不能吃、极少作为工业原料、不会增加,从性质上就和我们这里讨论的货币完全一致,我们这里就把黄金直接认为是货币。
|
||||
|
||||
现在考虑以下情况:
|
||||
|
||||
| 行为 | 做面粉的 | 做面包的 |
|
||||
| -------- | ------------------------------ | ---------------- |
|
||||
| 开始 | 初始货币 100 | 初始货币 100 |
|
||||
| 交易面粉 | 货币 +50(150) | 获得 50 斤面粉 |
|
||||
| 交易面包 | 货币-50(100),获得 25 个面包 | 货币 +50(100) |
|
||||
| 挖矿 | 货币 +20 | 货币 +20 |
|
||||
| 期末 | 120(25 个面包) | 120(25 个面包) |
|
||||
|
||||
几轮循环下来,面粉厂和面包厂都会拥有非常多的货币。
|
||||
|
||||
但显然,单纯有货币没有用,<strong>如果我们的系统里生产力不会提升,再多的货币也不能购买到超过 50 个面包</strong>。
|
||||
|
||||
我们来讨论一下,由于这里大家都有了很多储蓄<strong>,面粉厂和面包厂都会有一种自己可以消费更多面包、或者不用工作也不会饿死的错觉</strong>。
|
||||
|
||||
<strong>这种错觉是错误的,而它是如此的真实,一定会有人付诸实践,因此,这种错觉一定会被打破。</strong>
|
||||
|
||||
假设现在发生了第一种情况,面粉厂觉得自己有了很多储蓄,愿意多消费更多面包,而面包厂也不甘示弱,觉得自己如果要减少面包消费,卖出的额外的面包需要涨价。
|
||||
|
||||
假设面粉厂现在愿意以原价购买 25 个面包,额外还想购买 5 个面包,并与面包厂达成了协议,额外的部分每个付费 4 元,那么面包的价格就来到了 2.333 元,同样的,这种价格上涨也会导致双方认为自己的储蓄缩水,进而又回到工作的状态。
|
||||
|
||||
从上述的讨论中可以发现,<strong>货币增加后,面包的价格并不一定立即增长,价格的涨幅通常也与货币的增幅没有直接关系,而是买卖双方针对价格博弈的后果。但可以肯定的是,脉冲式的价格上涨一定会出现</strong>。
|
||||
|
||||
## 印钞部门
|
||||
|
||||
到目前为止的讨论都仅限于面粉厂与面包厂的交易,这里我们可以引入第三个经济部门,称为铸币部门。铸币部门不做别的事情,只是打造新的货币,并且我们假设铸币行为本身不需要成本。
|
||||
|
||||
假设铸币部门每期打造 4 枚货币
|
||||
|
||||
| 行为 | 做面粉的 | 做面包的 | 铸币部门 |
|
||||
| -------- | ------------------------------ | ---------------- | ------------------- |
|
||||
| 开始 | 初始货币 100 | 初始货币 100 | 0 |
|
||||
| 铸币 | | | 铸币 4 |
|
||||
| 交易面粉 | 货币 +50(150) | 获得 50 斤面粉 | |
|
||||
| 交易面包 | 货币-48(102),获得 24 个面包 | 货币 +52(102) | 购买 2 个面包(-4) |
|
||||
| 期末 | 102(24 个面包) | 102(24 个面包) | 0(2 个面包) |
|
||||
|
||||
上述现象的神奇之处在于,<strong>铸币部门不做任何工作就获得了面包分配,而面粉厂与面包厂在不了解经济运行全貌的情况下,总是认为自己是由于节俭而增加了储蓄</strong>。
|
||||
|
||||
剩下的问题同情况 2 所讨论的,储蓄的积累会带来脉冲式的价格体系变化。
|
||||
|
||||
## 贸易、分工、效用、货币沉积
|
||||
|
||||
到此为止,我们讨论的生产消费模型中人们都只是制造面包这一食物,但人的需要远比食物来的多,最基本的还有穿、住、行这三项没有满足。
|
||||
|
||||
假设有另一个村庄,他们看到了“穿”这个需求,并决定举全村之力生产衣物,卖给邻村。而食物的生产制造则完全交给邻村,他们不再生产面包。
|
||||
|
||||
这样,我们就引入了一个新的角色了,可以称之为“商人”。
|
||||
|
||||
“商人”实际不做产出,只是在两个村庄之间倒卖面包和衣物。假设商人每一期倒卖都能赚 40 元吧。同时,我们把做食品的合并为一个大的生产部门,同样把做衣服合并为一个大生产部门。应该发现,生产部门总是可以合并和拆分的。具体过程可以见下表:
|
||||
|
||||
| 行为 | 做面包的(甲村) | 做衣服的(乙村) | 商人 |
|
||||
| -------------- | ---------------------------------------------------- | ---------------------------------------------------- | -------------------- |
|
||||
| 开始 | 初始货币 100 | 初始货币 100 | 初始货币 20 |
|
||||
| 内部生产与消费 | 结余面包 10 | 结余衣物 10 | |
|
||||
| 商人倒卖面包 | 面包厂 +20 | -40(+10 面包) | +20(-20、+40) |
|
||||
| 商人倒卖衣物 | 面包厂-40 | +20 | +20(-20、+40) |
|
||||
| 期末 | 80(内部消费 40 个面包,售出 10 个,消费 10 件衣物) | 80(内部消费 40 件衣物,售出 10 件,消费 10 个面包) | 40(假设商人不消费) |
|
||||
|
||||
这里其实有很多问题可以讨论:
|
||||
|
||||
1. 我们可以再次感叹一下货币的伟大,因为有货币,所以乙村的衣物即使一件都卖不出去,也可以靠储蓄获得一定的面包,不至于被饿死
|
||||
2. 商人这个角色,实际上什么都没有产出,为什么他可以凭空获得 40 元的货币分配呢?一个初步的理解是,商人虽然没有产出,但是他通过倒卖行为优化了消费结构,提高了甲村和乙村的效用。
|
||||
3. 商人这个角色同时也是非常危险的,因为他仅凭一个人在一期时间内就获得了整个经济体系 20% 的货币,而这很可能是他无论如何消费都消费不完的。这意味着货币会在商人处发生沉积。货币沉积意味着经济系统中货币总量的下降,对于甲村和乙村的个体来说,就像是“经济不景气,收入不好”一样,会造成价格下降、消费下降等问题。货币沉积在金本位的经济制度中尤为严重,这也是以前的经济系统不稳定、政权经常崩盘的原因之一。
|
||||
|
||||
## 债务
|
||||
|
||||
最后,我们来讨论一下债务。
|
||||
|
||||
假设甲村的面粉厂要办喜事,需要多消费面包,但他并没有足够购买面包的储蓄,于是向面包厂借贷。这里的借贷行为,可以是借面包,也可以是借货币。另外,也可以是借面包还货币或者借货币还面包。情况比较复杂,这里简单讨论一下。
|
||||
|
||||
假设面粉厂这次想要额外消费 30 个面包,面包厂则愿意为喜事额外生产 5 个面包(总共生产 55 个面包,全部用于面粉厂消费),总共需要 60 元,但总共的储蓄只有 50 元,那么需要问面包厂要 10 元,购买面包厂的面包。
|
||||
|
||||
| 行为 | 面粉厂 | 面包厂 |
|
||||
| -------------------- | ----------- | ----------- |
|
||||
| 开始 | 初始货币 50 | 初始货币 50 |
|
||||
| 购买面粉 | +50 | -50 |
|
||||
| 购买面包(常规消费) | -50(50) | +50(50) |
|
||||
| 办喜事借贷 | +10(60) | -10(40) |
|
||||
| 办喜事消费 | -60(0) | +60(100) |
|
||||
| 期末 | 0 | 100 |
|
||||
|
||||
这样以来,可以看到面粉厂一下子失去了所有储蓄,假设面粉厂被要求在下一期还清债务 10 元。
|
||||
|
||||
| 行为 | 面粉厂 | 面包厂 |
|
||||
| -------------------- | ---------- | ------------ |
|
||||
| 开始 | 初始货币 0 | 初始货币 100 |
|
||||
| 购买面粉 | +50(50) | -50(50) |
|
||||
| 购买面包(常规消费) | -40(10) | +40(90) |
|
||||
| 还清债务 | -10(0) | +10(100) |
|
||||
| 期末 | 0 | 100 |
|
||||
|
||||
可以看到,这里看起来货币的结余情况一样,但实际上面粉厂减少了面包消费用于偿还债务,也就是说,<strong>通过上述描述货币和消费情况表格的表达方式,我们无法完整描述这一过程</strong>。在接下来,会引入简单的资产负债表,用于刻画这一过程。
|
||||
|
||||
可惜的是,从另一角度说,面粉厂接下来若要重新获得储蓄,需要在接下来的 4 期内都只消费 10 个面包,否则面粉厂就无法恢复储蓄。更何况,面包厂未必有意愿自己消费 60 个面包,因此,<strong>在这种古早的经济系统下,超前的借贷实际上会降低经济活力,形成经济不景气的现象</strong>。
|
||||
|
||||
从另一个角度来探讨,可以发现面粉厂还债的时候实际上是通过还面包的方式来进行还债的,由此,可以推出另一个结论:当经济系统中一方货币不足时,可以通过降低消费或者提供服务的方式来偿还债务,也就是说经济系统中的债务量可以大于经济系统中的货币数量。关于这部分内容,下文还会有一些讨论。
|
||||
|
||||
## 巨大工程与货币本质
|
||||
|
||||
甲村发展的越来越好,那么如果甲村想要建设一个价值 1000 元的村庄博物馆,他们应该怎么做呢?
|
||||
|
||||
这个问题可能看起来有些唐突了,价值 1000 元是什么意思呢?为什么在这里要加这个定语?
|
||||
|
||||
要回答这个问题,我们就需要讨论一下货币的本质是什么了。
|
||||
|
||||
考虑你想要买一只鸡来吃,在人类社会中,鸡是一种商品,而你拥有货币。看起来你拥有对鸡(商品)的支配权,但实际并非如此。因为你不能走进大山里用货币向大自然换一只鸡来,<strong>实际上,在你购买这个商品时付出的货币,是购买了打猎或者养殖鸡的人的劳动力,而非是购买了鸡这种商品本身</strong>。同样,价值 1000 元在上文的意思就是,如何建造一个需要 1000 元才能够买得到的劳动力才能建造的博物馆,而不是说博物馆本身价值 1000 元。
|
||||
|
||||
明白了这一点,就很好解释如何建造这个博物馆了,我们引入一个新的经济部门,叫建筑商,建筑商雇佣工人来完成博物馆的建设,每个工人的工资是 4 元,工人会把工资的全部都用来购买面包。所以,建造博物馆需要 1000/4=250 个人/期单位的劳动力。只要经济可以正常循环下去,每期都有工人来参与建设、获得面包,价值 1000 元的博物馆就可以建成。
|
||||
|
||||
## 小结
|
||||
|
||||
本节中简单讨论了最简单的生产-消费模型,引入了货币的概念,并引入了铸币税、贸易等基本的经济学概念。
|
||||
|
||||
本节最后,讨论了债务和货币沉积。在接下来的讨论中,会引入“银行”等新的经济实体,这会从根本上改变经济系统的运作方式。在此上下文下,货币沉积甚至是保证银行正常运行的基础、债务会带来经济繁荣。可以留意后文的讨论再来做对比。
|
||||
|
||||
## 思考题
|
||||
|
||||
1. 当前,中国的农村老人养老金很少遭到诟病,能否通过提升他们的养老金来提高他们的生活质量呢?养老金,或者说货币流通、再分配的本质是什么?
|
||||
|
||||
# 虚假的繁荣经济
|
||||
|
||||
## 生产余力与经济繁荣
|
||||
|
||||
假设甲村的人非常聪明,他们发明了一种能够全自动播种、收割小麦的机器,使得面粉的产量增加了 10%。现在甲村就有 3 个经济部门了。分别是:面粉厂、面包厂和农机厂。
|
||||
|
||||
假设面包的生产数量完全受限于面粉的数量,更多的面粉就意味着有更多的面包。一切看起来都很美好,人们有比以前更多的面包了,这意味着生活质量的改善、生产力的提高。
|
||||
|
||||
但这里还有一个问题没有解决,面粉厂为什么要生产更多的面粉呢?
|
||||
|
||||
现在消费意愿没有变,甲村还是每一期消费 50 个面包,仅仅是面粉厂获得了一种可以提高面粉产量的技术,既然面粉生产多了也卖不掉,面粉厂为什么要生产更多的面粉呢?
|
||||
|
||||
这里就要回到我们之前讨论过的[印钞部门](https://nq077wcre3.feishu.cn/docs/doccnisJfwYYDUqHJwTtBg6SB5b#pYjCEY)了,在这一节中,印钞部门通过印钞,提高了人们的消费意向。也就是说,在生产力提高的情况下,需要印钞部门(通常是政府)这一角色,来为促进消费尽一份力。具体的过程可以表示如下:
|
||||
|
||||
| 行为 | 做面粉的 | 做面包的 | 铸币部门 |
|
||||
| ------------ | ----------------------------- | ---------------------- | ------------- |
|
||||
| 开始 | 初始货币 50 | 初始货币 50 | 0 |
|
||||
| 铸币 | | | 铸币 10 |
|
||||
| 交易面粉 | 货币 +50(100) | 获得 50 斤面粉 | |
|
||||
| 交易面包 | 货币-50(50),获得 50 个面包 | 货币 +50(50) | |
|
||||
| 政府刺激消费 | 货币 +5,生产 5 斤面粉 | 货币 +5,售出 5 个面包 | -10(消费面包) |
|
||||
| 期末 | 55 | 55 | 0 |
|
||||
|
||||
虽然在这一期中,看起来是面粉和面包厂额外做了面包供政府消费,但实际上他们的储蓄有了增加,因此他们的消费意愿也会增加。
|
||||
|
||||
因此,只要政府部门能够敏锐地发现生产余力的存在,并且向经济系统中添加适量货币,就能够促进经济的发展,形成繁荣的经济现象。
|
||||
|
||||
<strong>可惜的是,要增加多少储蓄才能让人们有足够多的消费意愿这一问题根本无法准确回答,政府部门在这一过程中总是倾向于多发行货币,因此,这种情况下通常也会带来商品价格的上涨。</strong>
|
||||
|
||||
## 产出结构、资源分配
|
||||
|
||||
在上文提到,甲村现在有了个新的经济部门,农机制造部门。
|
||||
|
||||
农机制造部门生产的机器非常伟大,能够提高小麦产量,提高人们的幸福水平。
|
||||
|
||||
但,农机制造部门会因此得到资源倾斜、产出更好的农机吗?我们来考察一下这个问题。
|
||||
|
||||
假设农机部门从无到有创造了行业,但现在并没有什么需求,还要等待政府部门意识到生产力的提高和货币不足,因此,农机的加个并不能设置得很高,否则一定不会有面粉厂买,无异于自杀。
|
||||
|
||||
就假设一台农机可以耕作一单位的土地,使这一单位土地的面粉产量增加 10%,面粉厂一共有 10 单位土地,要让整体产量增加 10%,需要 10 台农机,一台农机最后定价 4 元,农机厂每期生产 1 台农机。
|
||||
|
||||
定价 4 元这一动作,其实就是说经济系统内的其他部门花 2 个面包供养农机厂,农机厂消费 2 个面包,产出一台农机。
|
||||
|
||||
在这里,暂时不考虑 4 元这个定价是否合理,<strong>可以发现虽然农机厂生产的农机本身可以提高面包产量,但最终农机厂得到的供养却与</strong><strong>起</strong><strong>贡献的面包产量不成正比</strong>。而且,可以预见的是,在出售 10 台农机后,农机就不会被需要,这意味着农机厂若没有依靠这 10 期的供养产出更高效的农机就会被放弃供养而倒闭。
|
||||
|
||||
<strong>这一事实说明经济系统的运行规则存在其固有缺陷,并不一定可以把资源倾斜给实际提供产出的部门,相反,随着面包产量增加、政府增发货币,农机厂可能是收入提升最少的,意味着农机厂获得的资源分配会越来越少。</strong>
|
||||
|
||||
## 不可能的指数增长
|
||||
|
||||
我们总是用指数化的方式来描述经济的增长,总说这一期的产量较上一年增长了多少百分比。但若仔细考虑增长的来源,就能发现指数增长是不可能实现的,并且衰减通常来得非常快、衰减幅度也会非常大。
|
||||
|
||||
考虑农机厂现在由于政府干预受到了足够的重视,决定开始加速农机产出,使得每一期农机保有量都比上一期多 50%。面粉厂也十分努力,在原先 10 单位的土地之外,开垦新土地,每一期土地的面积都比上一期多 10%。需要注意,这已经是非常非常高、近乎不可能实现的增长速度,所以这是一个人们都非常努力的经济体,大家都在努力工作追求经济增长。
|
||||
|
||||
我们可以做一个表,描述土地和农机的增长过程
|
||||
|
||||
| 期数 | 农机保有量 | 土地面积 | 缺口 |
|
||||
| ---- | ---------- | -------- | ----- |
|
||||
| 1 | 1 | 10 | 9 |
|
||||
| 2 | 1.5 | 11 | 9.5 |
|
||||
| 3 | 2.25 | 12.1 | 9.85 |
|
||||
| 4 | 3.375 | 13.31 | 9.935 |
|
||||
| 5 | 5.0625 | 14.64 | 9.58 |
|
||||
| 6 | 7.59 | 16.10 | 8.51 |
|
||||
| 7 | 11.385 | 17.71 | 6.325 |
|
||||
| 8 | 17.0775 | 19.481 | 2.40 |
|
||||
| 9 | 25.61 | 21.42 | -4.18 |
|
||||
|
||||
可以发现,一开始,不论大家如何努力生产,缺口都保持在 9 以上,甚至还有扩大的趋势,但随着时间推移,很快在第 9 期就迎来了经济衰退,经济系统不再需要这么多农机,在现行的经济评价指标下可以认为是经济陷入了衰退。
|
||||
|
||||
<strong>仅从上表就不难看出,追求指数增长是不可能的,经济体通常会在极短的时间以出乎所有人预料的速度内陷入衰退。</strong>
|
||||
|
||||
除此之外,我们可以从实际增长方式的角度论证指数增长是不可能的。
|
||||
|
||||
假设农机厂依赖机床来进行农具的生产,一台机床在 1 期可以产出 1 台农具。机床是高精尖产物,每期只能生产一台。那么就有在 t 期的农机保有量=t + t-1 + t-2 + t-3 + ... + 1 = (t + t^2)/2,是一个二次函数。面粉产量与 t 的关系也是一个二次函数。而当我们用指数增长与二次函数的增长速度相比较时,就会发现在早期,指数函数增长总比二次函数慢一些,而在之后,指数函数的增长速度会大幅超过二次函数。
|
||||
|
||||
## 经济繁荣周期
|
||||
|
||||
在本节的最后,来考虑一下竞技是如何变得繁荣的。
|
||||
|
||||
经济繁荣,其实就是指个体的储蓄增多,人们觉得赚钱很容易,觉得自己对商品的支配力变强。要出现这种情况,可能是生产力变得更发达,也可能是人们的账面资产得到了增加。通常,在经济繁荣周期中,这两种现象总是夹杂着出现、互相放大彼此。
|
||||
|
||||
首先,由于生产力有了一些发展,政府会增加货币投放,货币增加使得人们的账面资产增加,而这时处于经济繁荣的初期,商品的价格并没有怎么上涨,人们会发现自己的钱能够买到比以前更多的商品,相信自己拥有了更强的商品支配力。
|
||||
|
||||
这时,通常会出现一个极速涨价的金融资产,由于大家有了更多储蓄,大家都倾向于投资金融资产,在很多场景下,这个金融资产是房地产。
|
||||
|
||||
由于金融标的账面价格的进一步上涨,人们会相信自己拥有了更多的财富,这时,即使物价开始出现比较明显的上涨,人们也会觉得金融标的的上涨速度远大于物价,在这一步中,资产的账面价格上涨促进了经济繁荣。
|
||||
|
||||
在经济繁荣周期的中后期,人们会惊讶地发现生活必需品(通常又是房子)的价格大幅上涨,已经超过了人们收入的增长速度,于是此时面临一个抉择,如果大部分人选择在此时降低自己的消费、提高自己的储蓄,那么大量账面资产的价值就会无法兑现,会加速经济繁荣周期的结束。
|
||||
|
||||
反之,如果人们面对生活必需品价格的上涨,选择对生产的物品也涨价(例如,煎饼果子涨价),以此来提高储蓄速度,那么经济体系会迎来又一波整体的价格上涨。
|
||||
|
||||
最终,经济繁荣周期一定会结束,但何时结束,取决于人们的价格博弈结果,如果人们一直选择涨价,终究会有收入分配不合理的群体首先无法支撑价格上涨开始进入削减消费周期。
|
||||
|
||||
从上述讨论中不难发现,经济系统实际上并没有自限性地防止价格过度上涨的机制,而通常在经济繁荣周期结束后,也没有让价格对应下调的机制。这意味着在经济繁荣周期结束后,经济体通常会进入滞涨周期。在滞涨周期中,资产的价格长期维持高位,人们通过发展生产力、再分配等手段来促进价格体系回归正常,因此,滞涨周期也可以理解为价格体系的修复周期。
|
||||
|
||||
# 下一篇&本篇总结
|
||||
|
||||
在本篇中,我们简单建立了一个经济系统的模型。并利用这个模型,演示了现实生活中发生的各种事件和其对系统的影响。
|
||||
|
||||
需要注意的是,这个经济模型并不是我们现在的经济模型,因为其中并没有引入现代经济系统中非常重要的银行部门,没有产生大量的信贷。
|
||||
|
||||
因此,这个模型中的“经济景气”情况并不容易出现,同时,超前借贷等情况反而会给经济增长带来巨大压力。这显然并非现在的情况。
|
||||
|
||||
在下一篇中,会引入银行部门来构建一个更现代的经济系统,并简单论述银行这一经济部门的特点和风险。
|
||||
112
8.基础学科/8.2定积分.md
Normal file
112
8.基础学科/8.2定积分.md
Normal file
@@ -0,0 +1,112 @@
|
||||
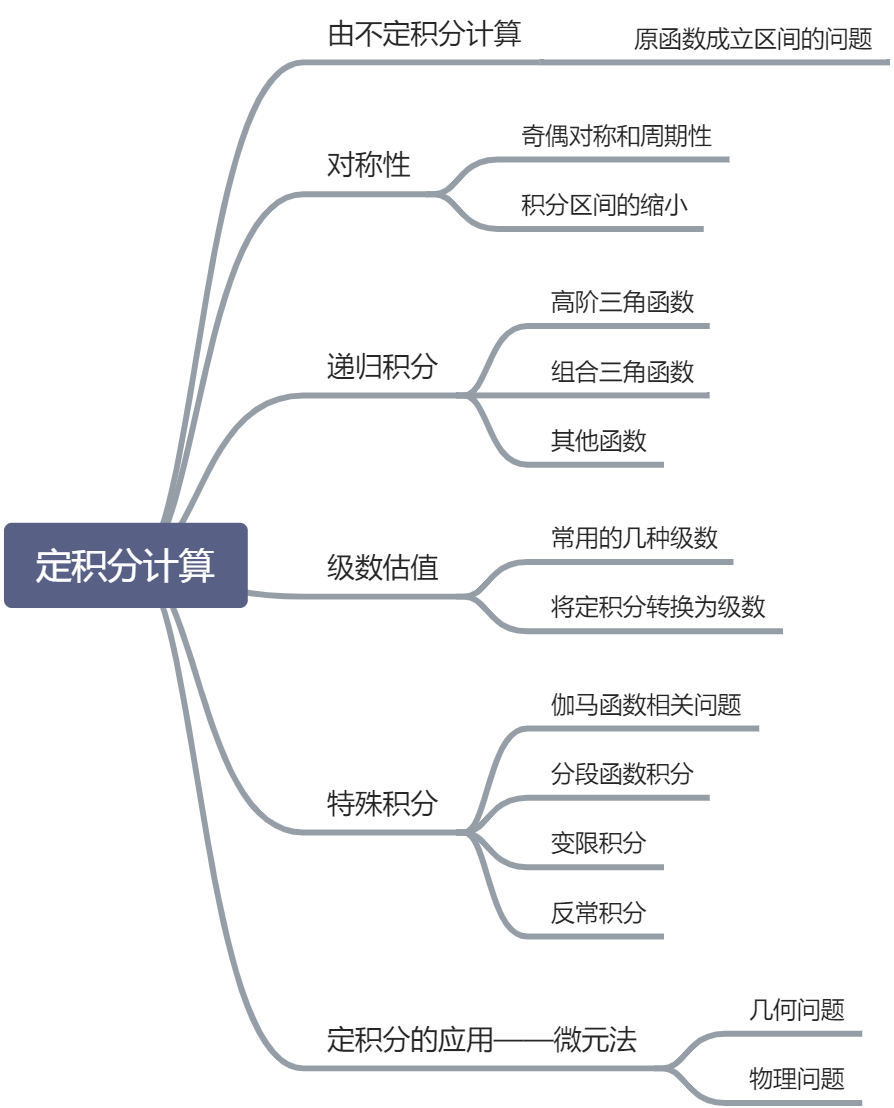
本文主要讲解定积分在计算时运用的各种化简技巧。
|
||||
<a name="Q47Sf"></a>
|
||||
# 一:由不定积分计算定积分
|
||||
|
||||
<a name="9HiLn"></a>
|
||||
## 1.1原函数成立区间的问题
|
||||
|
||||
注意:由不定积分推导出的原函数在定积分的区间不一定成立!!!<br />对于大多数定积分题目,可直接由代入不定积分的结论。
|
||||
|
||||
<a name="JXXVa"></a>
|
||||
# 二:利用对称性化简定积分
|
||||
|
||||
<a name="RHvOT"></a>
|
||||
## 2.1奇偶对称和周期性
|
||||
|
||||
<br />命题1:设函数f在区间$[0,a]$可积,且关于区间中点$\frac{a}{2}$为奇函数,即对于$x\in[0,a]$,有$f(x)=-f(a-x)$,则成立<br />$\int_0^af(x)dx=0$。<br />命题2:设函数f在区间$[0,a]$可积,且关于区间中点$\frac{a}{2}$为偶函数,即对于$x\in[0,a]$,有$f(x)=f(a-x)$, 则成立<br />$\int_0^af(x)dx=2\int_0^{\frac{a}{2}}f(x)dx$。<br />命题3:若函数f为定义在$-\infty<x<+\infty$上的周期为T的连续周期函数,即$f(x)$满足:$f(x)=f(x+T)$,则成立<br />$\int_a^{a+T}f(x)dx=\int_0^Tf(x)dx$<br />**_Proof:_**<br />将积分区间拆成多段,带入上文对称公式,之后换元即可,证明的本质是统一了积分区间。<br />_**Example:**<br />$\int_0^{2\pi}\frac{dx}{sin^4x+cos^4x}$
|
||||
|
||||
利用:$sin^4x+cos^4x=(sin^2x+cos^2x)^2-2sin^2xcos^2x=1-\frac{1}{2}sin^2(2x)=\frac{1}{2}(1+cos^2(2x))$,周期为$\pi/2$<br />两次利用命题3,将积分区间化简为$[0,\frac{\pi}{2}]$。由于被积函数关于$\pi/4$偶对称,利用命题2,可将积分区间化简为$[0,\frac{\pi}{4}]$,故原式等于:<br />$4\int_0^{\frac{\pi}{2}}\frac{dx}{sin^4x+cos^4x}=8\int_0^{\frac{\pi}{4}}\frac{dx}{sin^4x+cos^4x}=16\int_0^{\frac{\pi}{4}}\frac{dx}{1+cos^2(2x)}=8\int_0^{\frac{\pi}{2}}\frac{dt}{1+cos^2(t)}=8\int_0^{\frac{\pi}{2}}\frac{d(tant)}{2+tan^2t}$<br />$=8\int_{0}^{+\infty}\frac{du}{u^2+2}=4\sqrt{2}arctan(\frac{u}{\sqrt{2}})|_0^{+\infty}=2\sqrt{2}\pi$_
|
||||
<a name="KG0We"></a>
|
||||
## 2.2积分区间的缩小
|
||||
|
||||
命题4:设f在$[0,a]$上可积,则成立$\int_0^af(x)dx=\int_0^{\frac{a}{2}}[f(x)+f(a-x)]dx$,此为命题1,2的推广形式。<br />可推广为:$\int_a^bf(x)dx=\int_a^{\frac{a+b}{2}}[f(x)+f(a+b-x)]dx$,该命题在$f(x)+f(a+b-x)$更好积分时使用。<br />**_Proof:_<br />反向利用命题2,$\int_0^af(x)dx=\frac{1}{2}(\int_0^af(x)dx+\int_0^af(a-x)dx)=\int_0^{\frac{a}{2}}[f(x)+f(a-x)]dx$<br />命题5:若f(x)在闭区间$[0,1]$上连续,则<br />(a)$\int_0^{\frac{\pi}{2}}f(sinx)dx=\int_0^{\frac{\pi}{2}}f(cosx)dx$<br />(b)$\int_0^{\pi}xf(sinx)dx=\frac{\pi}{2}\int_0^{\pi}f(sinx)dx$<br />(c)$\int_0^{\pi}f(sinx)dx=2\int_0^{\frac{\pi}{2}}f(sinx)dx$<br />**_Proof:_**<br />(a)$x=\pi/2-t$,(b)$x=\pi-t$,(c)$t=x-\pi/2$<br />也可由命题4直接推出,如对于(b)<br />$\int_0^{\pi}(x-\pi/2)f(sinx)dx=\int_0^{\frac{\pi}{2}}(x-\pi/2+\pi-x-\pi/2)f(sinx)dx=0$<br />_**Example1:**_<br />(a)$\int_0^{\pi/2}\frac{sinx}{sinx+cosx}dx$ (b)$\int_0^{\pi/2}ln(sinx)dx$ (c)$\int_0^{\pi/2}ln(tanx)dx$<br />(d)$\int_0^{\pi/2}\frac{1}{1+tan^ax}dx$ (e)$\int_0^{\pi}\frac{xsinx}{1+cos^2x}dx$ (f)$\int_0^1\frac{lnx}{\sqrt{1-x^2}}dx$<br />例如,对于b,利用命题4,$\int_0^{\frac{\pi}{4}}[ln(sin(x))+ln(cos(x))]dx=\int_0^{\frac{\pi}{4}}[ln(sin(2x)/2]dx$<br />$=\int_0^{\frac{\pi}{4}}[ln(sin(2x))-ln(2)]dx=\frac{1}{2}\int_0^{\frac{\pi}{2}}ln(sin(x))dx-\frac{\pi}{4}ln2=-\frac{\pi}{2}ln2$<br />_**Example2:**_<br />设$f(x)$在$[a,b]$上连续且单调增加,证明:$\int_a^bxf(x)dx\geq\frac{a+b}{2}\int_a^bf(x)dx$<br />$\int_a^b(x-\frac{a+b}{2})f(x)dx=\int_a^{\frac{a+b}{2}}[(x-\frac{a+b}{2})f(x)+(a+b-x-\frac{a+b}{2})f(a+b-x)]dx$<br />$=\int_a^{\frac{a+b}{2}}(x-\frac{a+b}{2})[f(x)-f(a+b-x)]dx$<br />因为$f(x)$单增,所以$f(x)-f(a+b-x)\leq0$,原式大于等于0,证毕。
|
||||
<a name="ScUek"></a>
|
||||
# 三:利用递归表达式化简定积分
|
||||
|
||||
注意:全部利用分部积分构造递推表达式,使得分部积分脱出积分号的项为0,对积分内指数进行降阶即可。
|
||||
<a name="3sJIQ"></a>
|
||||
## 3.1高阶三角函数
|
||||
$I_0=\int_0^{\pi/2}dx=\pi/2$,$I_1=\int_0^{\pi/2}sinxdx=1$,$I_2=\int_0^{\pi/2}sin^2xdx=\pi/4$<br />思考:如果$I_n$为一数列$I_n=\int_0^{\pi/2}sin^nxdx$,请问<br />(1)$I_n$的递推表达式为?<br />(2)$I_n$的通项表达式为?<br />(3)$I_n(n\to\infty)$的极限为?<br />(4)求$\lim_{k\to\infty}\frac{I_{2k+1}}{I_{2k}}$?<br />答案:<br />(1),(2)<br />
|
||||
|
||||
推论:由命题4得,对cosx做上述操作得到结果相同。<br />(3)$I_n(n\to\infty)$的极限为0,如图为$sin^n(x)在[0,1]$的函数图像,因为$sin^n(x)<x^n<1$,所以函数在[0,1]为0,在x=1处为1,为非一致收敛的情况。,因此分成两段进行证明。<br />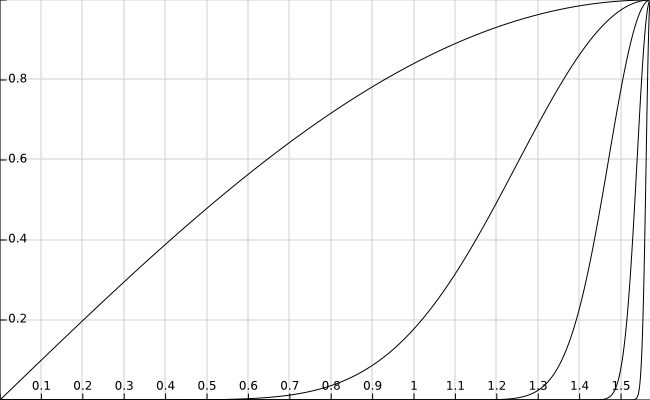<br />证明:<br />法一:积分的有界性<br />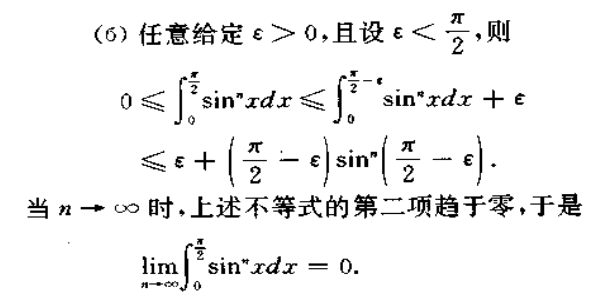<br />这里第二项趋于0是因为$sin^n(x)\to0$,从图中也可以观察出来。<br />法二:<br />$if\ n=2k$<br />$I_{2k}=\frac{(2k-1)!!}{(2k)!!}=\frac{(2k-1)\cdot(2k-3)\cdot\cdot\cdot5\cdot3\cdot1}{(2k)(2k-2)\cdot\cdot\cdot6\cdot4\cdot2}\cdot\frac{\pi}{2}$<br />$0<I_{2k}^2=\frac{1\cdot 3}{2^2}\cdot\frac{3\cdot 5}{4^2}\cdot\cdot\frac{(2k-3)(2k-1)}{(2k-2)^2}\cdot \frac{2k-1}{(2k)^2}\cdot\frac{\pi^2}{4}<\frac{2k-1}{(2k)^2}\cdot\frac{\pi^2}{4}\to0$<br />$\therefore I_{2k}\to0$<br />$\therefore I_{2k+1}=\int_0^{\pi/2}sinx\cdot sin^{2k}xdx=sinx_0\cdot\int_0^{\pi/2}sin^{2k}xdx\to0$<br />$\therefore I_{n}\to0$<br />(4)<br /><br />维基百科:[沃利斯乘积](https://zh.wikipedia.org/wiki/%E6%B2%83%E5%88%A9%E6%96%AF%E4%B9%98%E7%A7%AF)<br />3B1B:[沃利斯乘积的几何解释](https://www.bilibili.com/video/av22808876/)
|
||||
<a name="RTgjo"></a>
|
||||
## 3.2组合三角函数
|
||||
注意:此类题一律用分部积分画出和原被积函数相关的表达式,但不一定是相等,以实现得到递推关系降阶的目的。<br />_**Example:**_<br />求 $L_n=\int_0^{\pi/2}cos^n(x)cos(nx)dx$ 的递归表达式和通项<br />$=\frac{1}{n}\int_0^{\pi/2}cos^n(x)dsin(nx)=\frac{1}{n}(cos^n(x)sin(nx)|_0^{\pi/2}-\frac{1}{n}\int_0^{\pi/2}nsin(nx)cos^{n-1}(x)(-sin(x))dx$<br />$=\int_0^{\pi/2}cos^{n-1}(x)sin(nx)sin(x)dx$<br />$2L_n=\int_0^{\pi/2}[cos^{n-1}(x)sin(nx)sin(x)+cos^n(x)cos(nx)]dx=\int_0^{\pi/2}cos^{n-1}(x)(cos(nx)cos(x)+sin(nx)sin(x))dx$$=\int_0^{\pi/2}cos^{n-1}(x)cos((n-1)x)dx=L_{n-1}$<br />所以 $L_n=\frac{1}{2}L_{n-1}$ 而$L_1=\int_0^{\pi/2}cos(x)cos(x)dx=\pi/4$<br />所以数列的通项表达式为:$L_n=\frac{\pi}{2^{n+1}}$
|
||||
<a name="eHWDx"></a>
|
||||
## 3.3其他函数
|
||||
_**Example:**_<br />求 $I_n=\int_0^1x^m(ln(x))^ndx$ 的递推表达式和通项。
|
||||
|
||||
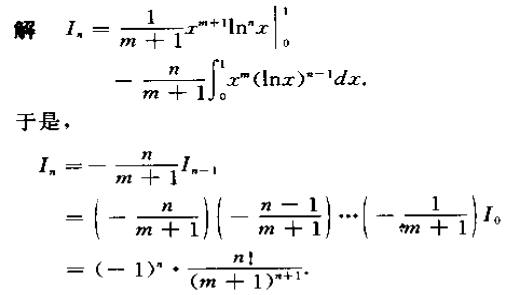<br />_**Exercise:**_<br />_****(3)求$a_n$的极限<br /><br />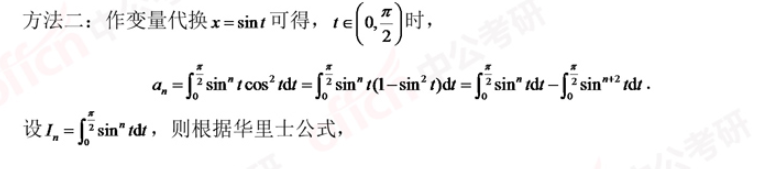<br /><br />(3)结果为0,证法和高阶三角函数一样。
|
||||
<a name="P1sfa"></a>
|
||||
# 四:利用级数对定积分进行估值
|
||||
|
||||
<a name="kHp6e"></a>
|
||||
## 4.1常用的几种级数
|
||||
基本的思路是:把函数做泰勒展开,交换积分和求和符号,对每一项幂函数进行积分,最后合并即可。<br />下面给出三个重要常数:
|
||||
|
||||
(a)$\sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}$ (b)$\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}=ln2$ (c)$\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{(2m-1)^2}\approx0.92$
|
||||
|
||||
此类级数可由初等函数泰勒展开后将x=1或x=-1代入得到。
|
||||
|
||||
这里给出简单的证明:<br />(a)$\sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}$<br /><br />(b)$\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}=ln2$ <br />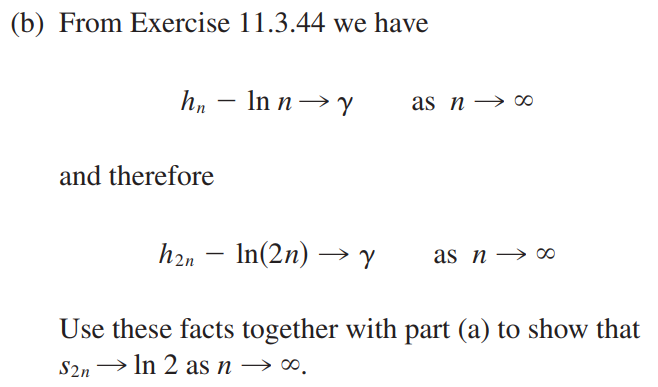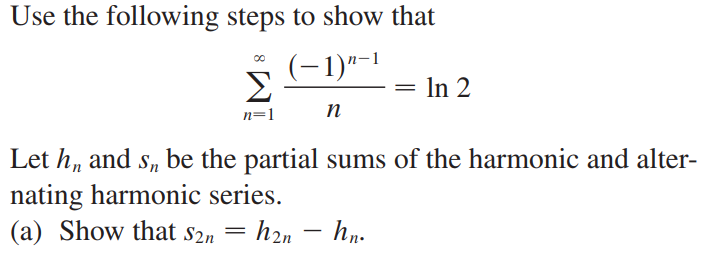
|
||||
|
||||
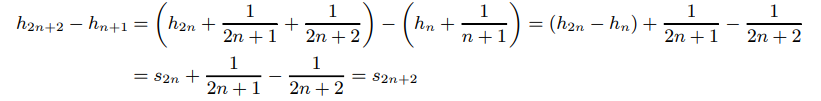<br />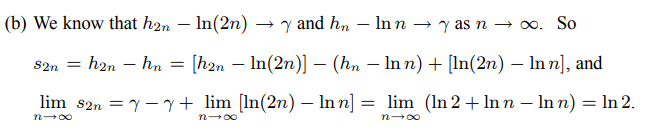 <br />(c)$\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{(2m-1)^2}\approx0.92$<br />$\int_0^1\frac{arctan(x)}{x}dx=\int_0^1\frac{1}{x}\sum_{n=0}^{\infty}(-1)^n\frac{1}{2n+1}x^{2n+1}dx=\int_0^1\sum_{n=0}^{\infty}(-1)^n\frac{1}{2n+1}x^{2n}dx=\sum_{n=0}^{\infty}(-1)^n\frac{1}{2n+1}\int_0^1x^{2n}dx$$\sum_{n=0}^{\infty}(-1)^n\frac{1}{(2n+1)^2}x^{2n+1}|_0^1=\sum_{n=0}^{\infty}(-1)^n\frac{1}{(2n+1)^2}=G\approx0.92$ (这可以利用计算机对此积分估值得到)
|
||||
|
||||
在计算积分时,通常通过上述思路把积分化为上述重要常数,进而直接得出结果。
|
||||
|
||||
<a name="u2lJV"></a>
|
||||
## 4.2将定积分转换为级数
|
||||
_**Example1:重要常数(a)**_<br />$\int_0^1ln(x)ln(1-x)dx$<br />答案:<br />[视频链接](https://www.youtube.com/watch?v=q9jbmEGClSk&list=PLj7p5OoL6vGzJxJU1seMmj-5CBNhMYStQ&index=8)<br />_**Example2:重要常数(c)**_<br />(a) $\int_0^{\pi/4}ln(tan(x))dx$ (b) $\int_0^{\pi/4}ln(cot(x))dx$<br />对于(a),令$t=tan(x)$ ,换元后可得:<br />$\int_0^1ln(t)d arctan(t)=[ln(t)arctan(t)]|_0^1-\int_0^1arctant\frac{dt}{t}=-\int_0^1arctant\frac{dt}{t}=-G\approx-0.92$
|
||||
|
||||
<a name="gTeyn"></a>
|
||||
# 五:特殊积分
|
||||
|
||||
<a name="xksxJ"></a>
|
||||
## 5.1伽马函数
|
||||
<br />维基百科点击下方链接:<br />[WIKI百科](https://zh.wikipedia.org/wiki/%CE%93%E5%87%BD%E6%95%B0)<br />下面为详细的视频教程<br />1:定义伽马函数<br />[视频链接](https://www.youtube.com/watch?v=L4Trz6pFut4&t=21s)<br />2:$(\frac{1}{2})!$<br />[视频链接](https://www.youtube.com/watch?v=dBmApl6gkII&t=5s)<br />3:$(-1)!$<br />[视频链接](https://www.youtube.com/watch?v=MfP2FQPBdHI&t=294s)<br />4:$n!!$<br />[视频链接](https://www.youtube.com/watch?v=imcooZyo4vE)
|
||||
<a name="kCups"></a>
|
||||
## 5.2分段函数积分
|
||||
此类题目的关键是原函数的连续性要求,通过待定系数求解,具体见不定积分中的[特殊积分部分](https://www.yuque.com/uhhida/tcgb6r/dg7du1)。
|
||||
<a name="GuHd2"></a>
|
||||
## 5.3变限积分
|
||||
形如$I(x)=\int_a^xf(t)dt$ 的积分叫做变限积分,他的本质是一个自变量在积分限的函数。<br />变限积分的求导法则尤其重要。此类题目需要扎实的数学分析思想,极其易错,具体内容见[积分证明框架](https://www.yuque.com/uhhida/tcgb6r/pcc7t2)。
|
||||
<a name="lr1ZN"></a>
|
||||
## 5.4反常积分
|
||||
具体内容见[积分证明框架](https://www.yuque.com/uhhida/tcgb6r/pcc7t2)
|
||||
<a name="AZJ0a"></a>
|
||||
# 六:定积分的应用
|
||||
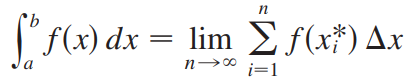<br />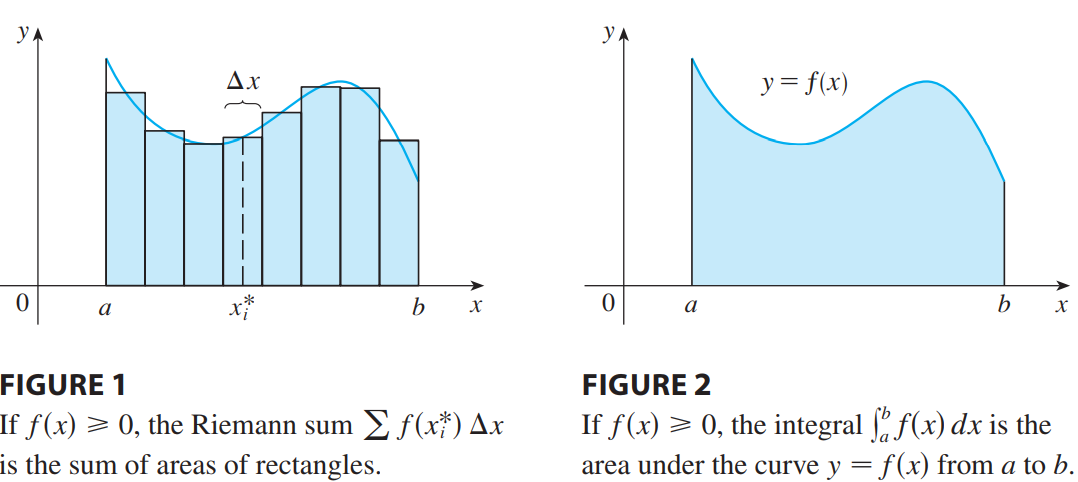<br />我们可以看到定积分的本质就是微元法取极限,所以一些几何和物理问题都可以用微元法的思想解决。<br />_**Example1:**_<br />已知一段半圆弧电荷密度为+1,计算圆心处的电场强度。<br />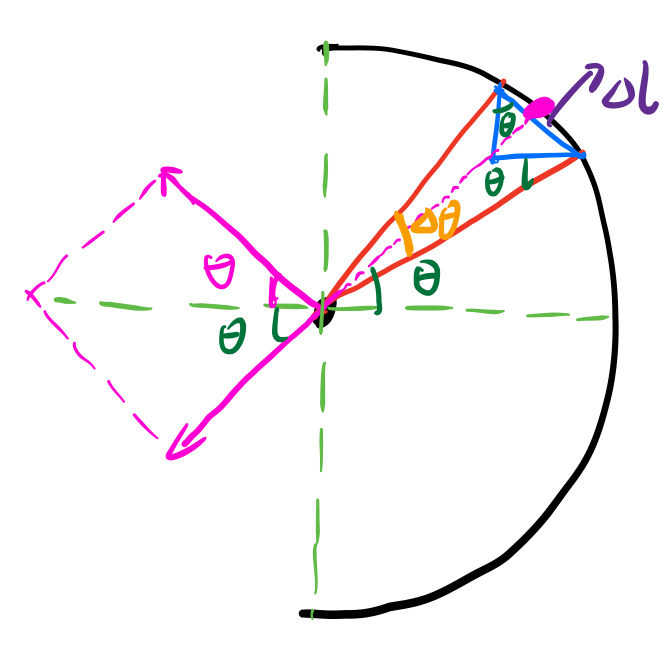<br />注意,这类题目直接用几何解法更快,由库仑定律得,两段对称的微弧对圆心的电场作用为:<br />$\Delta E=2\Delta E'cos\theta=\frac{2k\Delta lcos\theta}{R^2}=\frac{2k\Delta r}{R^2}$<br />$\Delta r$代表上图小三角形垂直部分,$\sum \Delta r=R$ ,所以:<br />$E=\sum\Delta E=\frac{2k}{R^2}\sum\Delta r=\frac{2k}{R}$<br />_**Example2:**_<br />我们可以利用微元法找到极坐标的面积公式<br /><br />
|
||||
<a name="bh4SN"></a>
|
||||
## 6.1几何问题
|
||||
<a name="oDven"></a>
|
||||
#### 6.1.1向量簇
|
||||
请下载:[New horizons in geometry(几何新视野).pdf](https://www.yuque.com/attachments/yuque/0/2019/pdf/422826/1564708063142-a6a603c9-ef19-42c5-bbac-3a746583ac46.pdf?_lake_card=%7B%22uid%22%3A%22rc-upload-1564707962520-4%22%2C%22src%22%3A%22https%3A%2F%2Fwww.yuque.com%2Fattachments%2Fyuque%2F0%2F2019%2Fpdf%2F422826%2F1564708063142-a6a603c9-ef19-42c5-bbac-3a746583ac46.pdf%22%2C%22name%22%3A%22New%20horizons%20in%20geometry(%E5%87%A0%E4%BD%95%E6%96%B0%E8%A7%86%E9%87%8E).pdf%22%2C%22size%22%3A9849775%2C%22type%22%3A%22application%2Fpdf%22%2C%22ext%22%3A%22pdf%22%2C%22progress%22%3A%7B%22percent%22%3A0%7D%2C%22status%22%3A%22done%22%2C%22percent%22%3A0%2C%22id%22%3A%227fZdG%22%2C%22card%22%3A%22file%22%7D)阅读第一章。<br />这里只讲一个拓扑定理:切线向量扫过的面积等于将这些向量在不改变方向和长度的情况下,将所有的向量尾部接到一起时所组成的图形的面积相等。即切线扫过的面积等于切线簇的面积,如图所示。<br />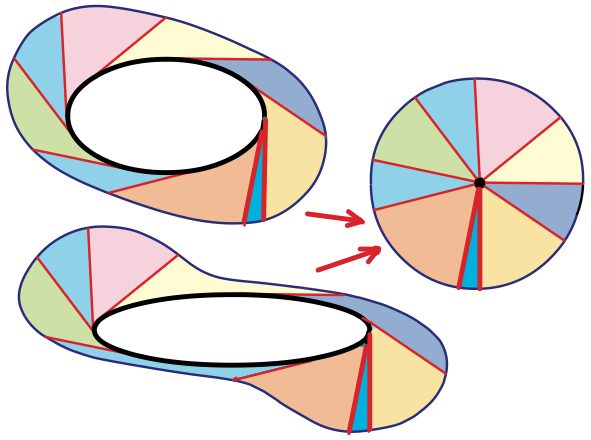<br />想象一辆自行车,其尾部车轮始终与某一闭合轨迹相切,也就是骑了一圈,那么无论骑行轨迹如何,自行车车身划过的面积始终不变。如上图所示,将一簇切线在不改变方向和长度的情况下尾部连接在一起,他们所组成的形状面积和原来扫过的面积相同,且原来图形的形状可以任意。<br />和开普勒第二定律及椭圆面积的关系:[视频链接](https://www.bilibili.com/video/av28012188)<br />_**Example3:**_<br />利用该定理证明$\int_{-\infty}^{x}e^{t/b}dt=be^{x/b}$<br />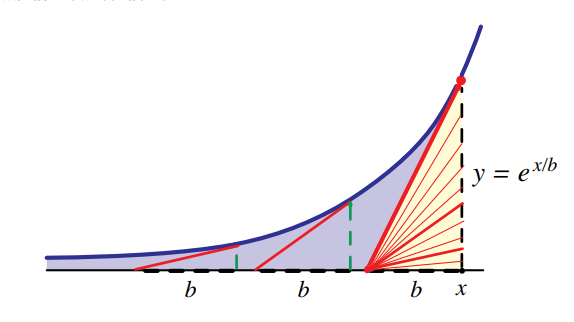<br />显然,所有切线构成的三角形底边长度都是1,把所有的切线全部放到黄色三角形内,尾部连接在一起,就得到积分的面积是两倍三角形的面积,即$be^{x/b}$。<br />_**Example4:**_<br />利用该定理求摆线下方的面积。<br /><br />摆线相关知识点击:[维基百科](https://zh.wikipedia.org/wiki/%E6%91%86%E7%BA%BF)<br />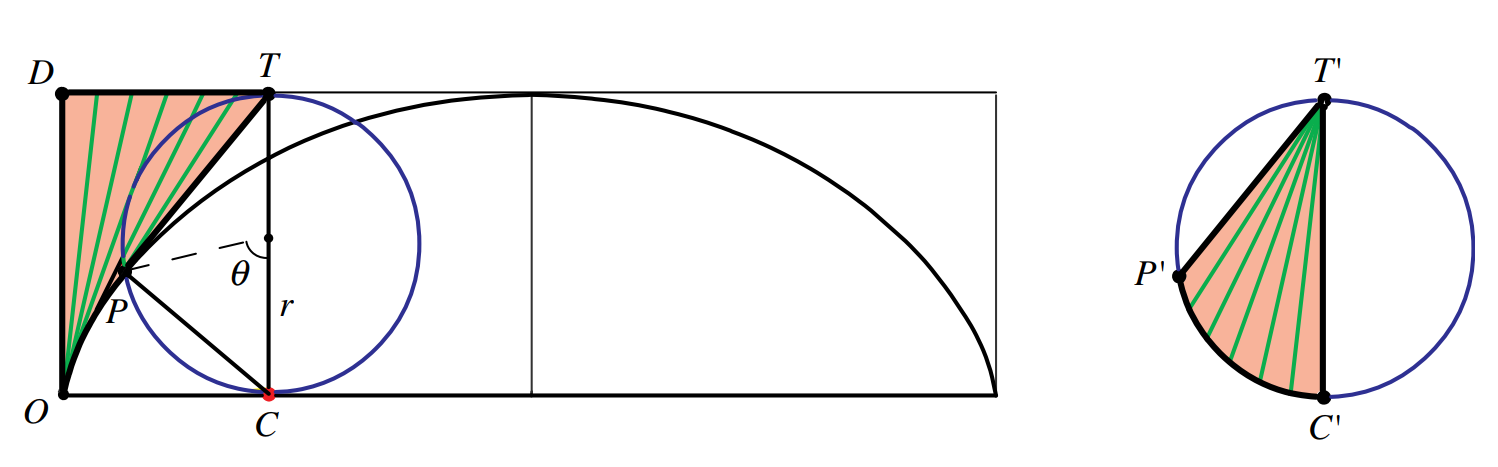<br />由于PT垂直于PC(在圆内),又因为点P在每个瞬时相对于点C做圆周运动,所以PT必然是点P的切向运动方向,所以PT也是摆线的切线,DOT的面积(及切线扫过的面积)等于右图中切线簇的面积(将所有切线平移到点T)。更具体的说,圆在运动时,点P划过了一段圆弧,在每一个中间点,都可以做线段PT,线段PT既扫过了DOT,也同时覆盖了T'P'C',故两者面积相等。<br />当圆旋转一周时,切线划过了整个摆线上方的面积,这面积等于切线簇的面积$\pi R^2$,而整个矩形的面积是$2\pi R\cdot 2R=4\pi R^2$,所以摆线下方的面积为$4\pi R^2-\pi R^2=3\pi R^2$。<br />利用参数方程的证明方法见下文。
|
||||
<a name="V1fjC"></a>
|
||||
#### 6.1.2体积
|
||||
这里依然是微元法,我们讲两种求旋转体体积的方法:切片法和圆柱法<br />**切片法:**<br />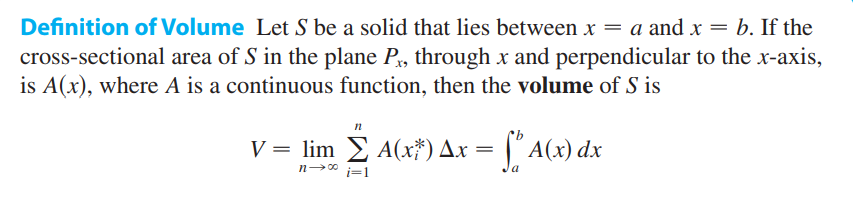<br />A(x)就是x处物体的面积,$\Delta x$就是高度,两者相乘就是和x有关的一个体积微元,求和或积分后就得到了整个体积。<br />_**Example5:**_<br />求$y=x$和$y=x^2$中间的部分绕$y=2$旋转一周所得到的图像的体积。<br />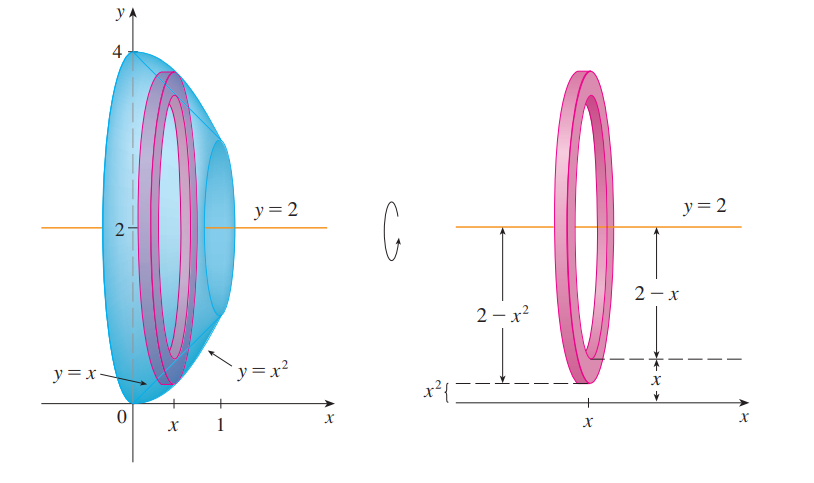<br />本题的关键是千万不要把正负号弄错,x和y的正负号永远是对原始图像而言的!!!<br /><br />_**Example6:**_<br />求$y=x$和$y=x^2$中间的部分绕$x=-1$旋转一周所得到的图像的体积。<br />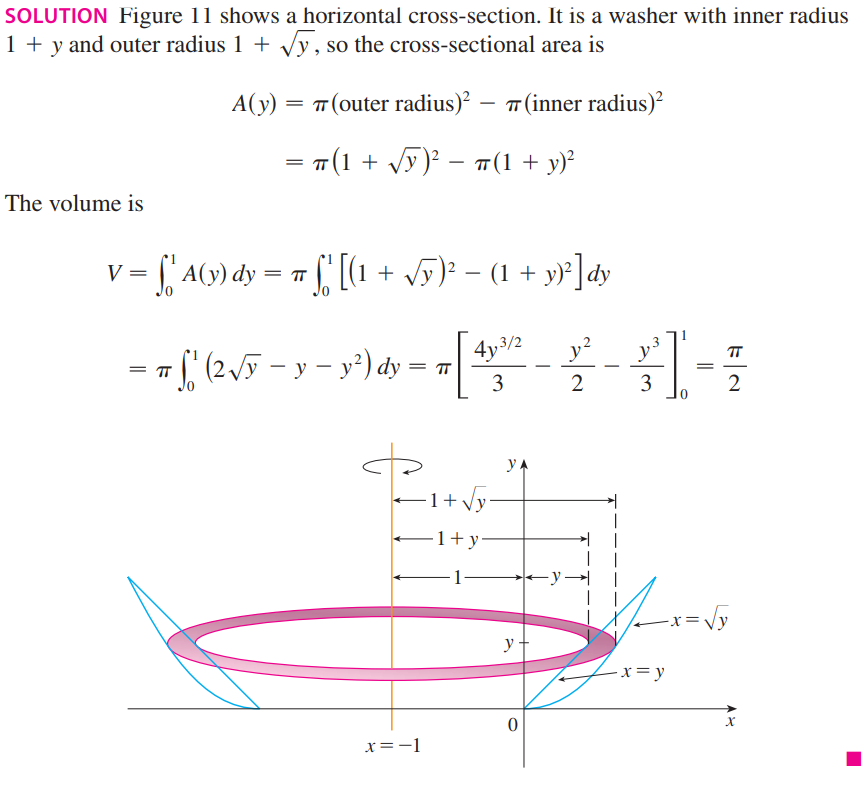
|
||||
|
||||
**圆柱法:**<br />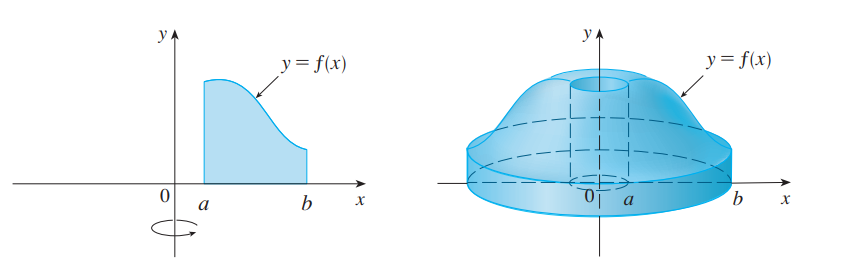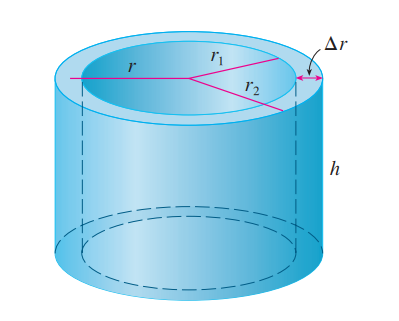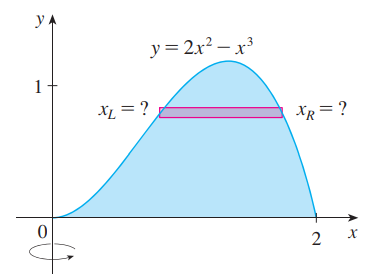<br />如图所示,$x_L和x_R$比较难求,当边界无法被解析式表达时,我们对垂直于旋转轴的底面做圆柱分解。<br /><br />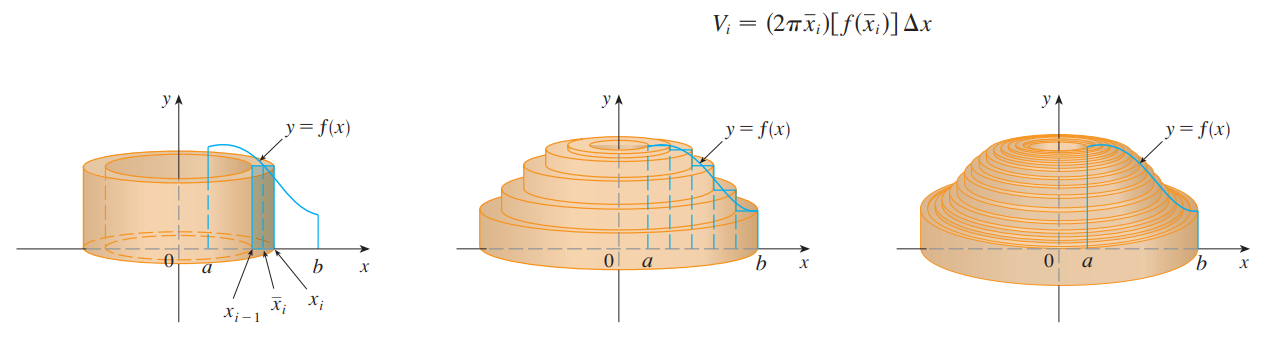<br /><br />一小段圆柱的体积=底面积:$2\pi xdx$ 乘以 高:$f(x)$,之后对自变量求积分。<br />_**Example7:**_<br />_****_<br />_**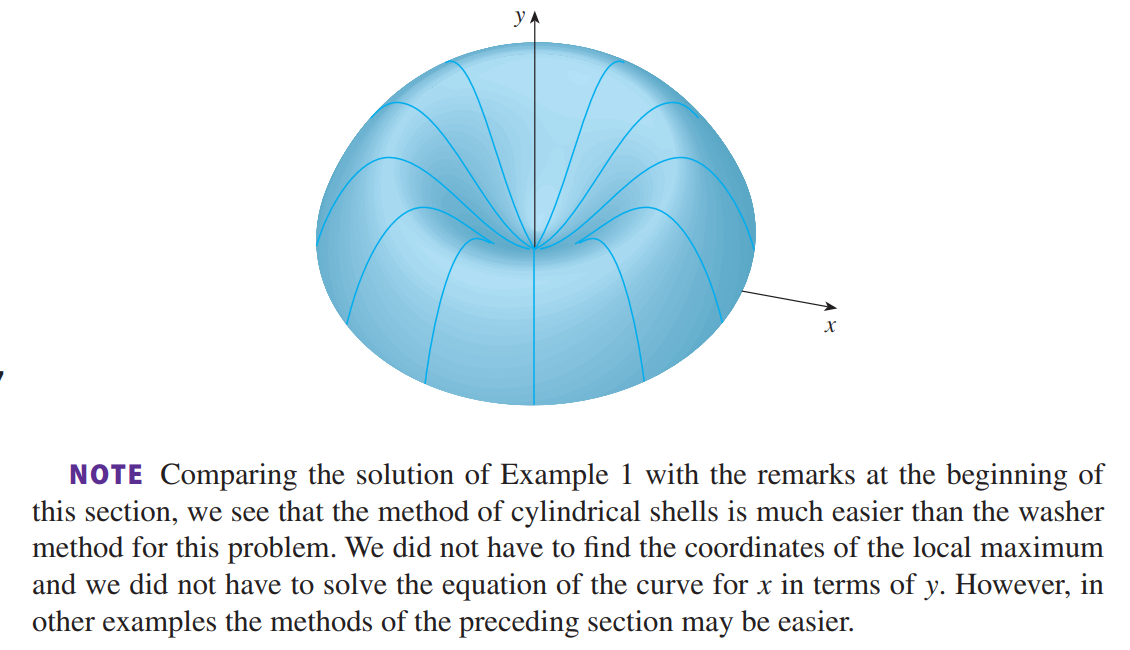**_<br />注意:在本题中,圆柱法比切片法简单的多,由于不用求边界,对于具体的题目,根据情况选择两种方法即可。_
|
||||
<a name="jM2iM"></a>
|
||||
#### 6.1.3弧长和表面积
|
||||
求弧长的方法十分显然,该方法也适用于极坐标,只需用微元法得到公式。<br />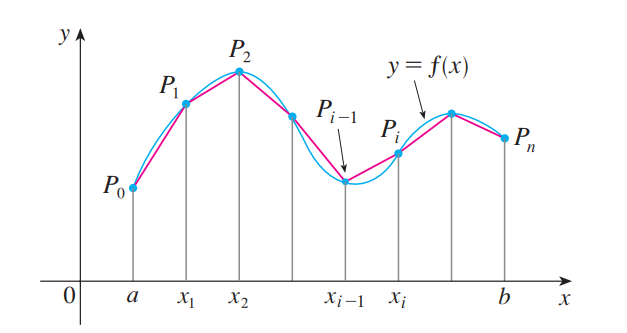<br />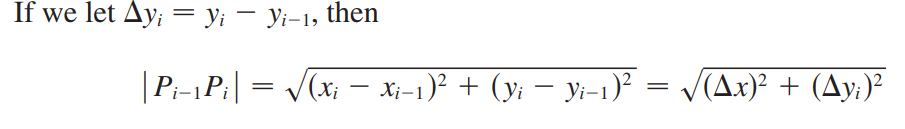<br /><br />求表面积的方法也是微元法,如下图所示:<br />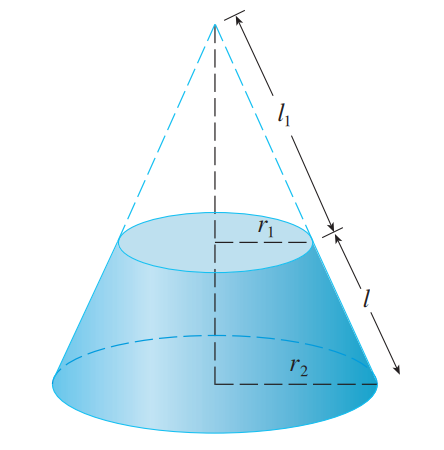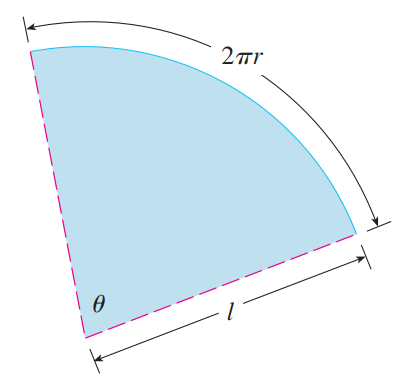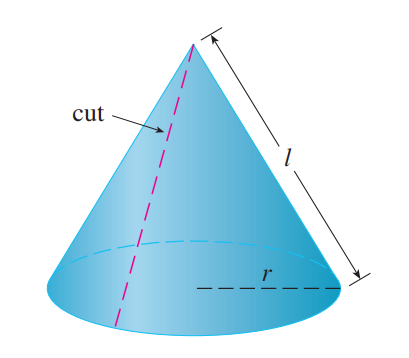<br />已知圆锥表面积是$\pi rl$,现在试图求解一段圆台的表面积,它等于两个圆锥相减。<br />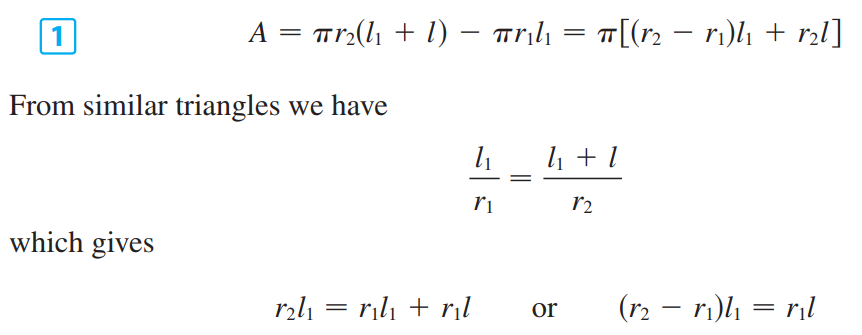<br /><br />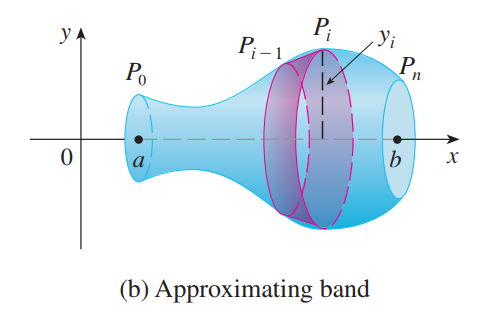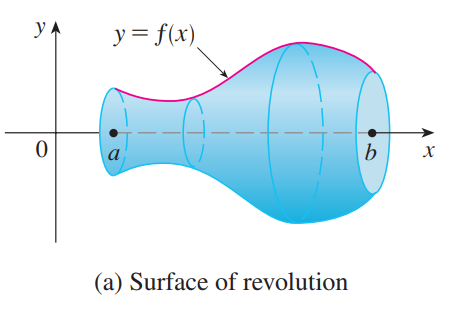<br />如上图所示,将任意旋转体分成无数小圆台,进行求和即可(这里为什么不能用圆柱做微元法?)。<br /><br />最后我们得到了表面积的表达式:<br /><br />_**Example8:**_<br />
|
||||
<a name="cRnev"></a>
|
||||
#### 6.1.4极坐标和参数方程
|
||||
**参数方程:**<br />参数方程本质就是把x和y想成某个变量t的函数,利用链式法则可以把微积分的计算用参数方程实现。<br />微分:<br />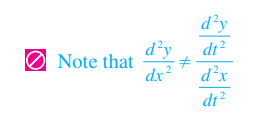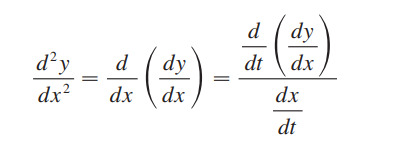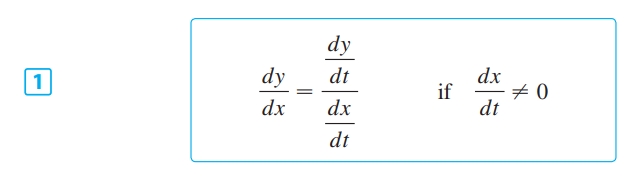<br />求面积:<br />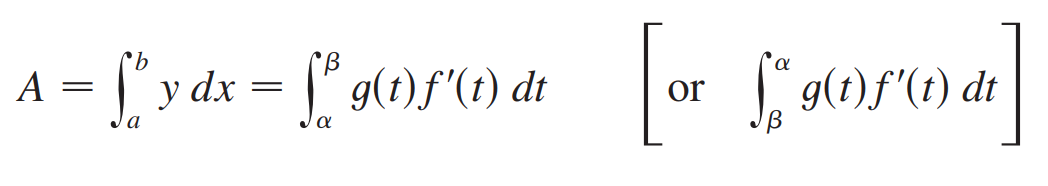<br />求长度:<br /><br />_**Example9:**_<br />我们以摆线为例,将摆线方程建模为关于转动角度的函数,如下图所示。<br />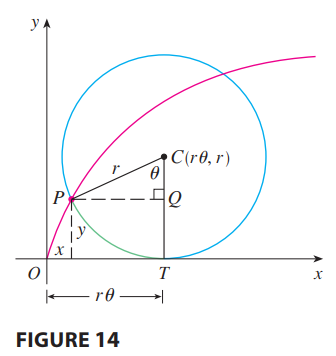<br /><br />摆线的面积:方法只是简单的换元。<br /><br />摆线的周长:<br /><br />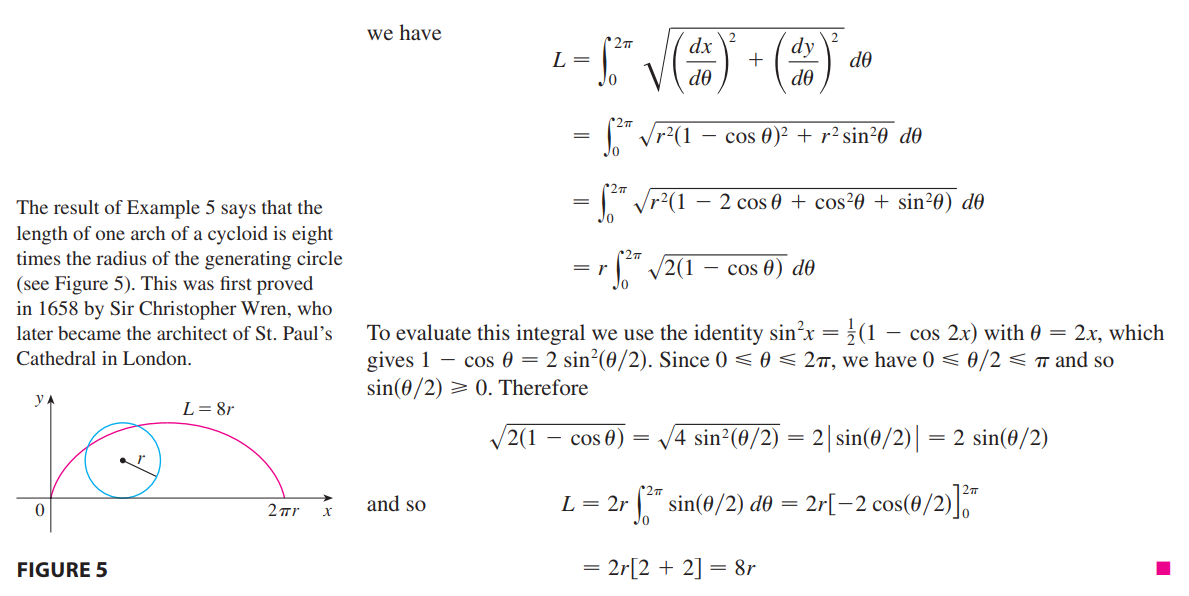<br />摆线相关知识点击:[维基百科](https://zh.wikipedia.org/wiki/%E6%91%86%E7%BA%BF)<br />摆线的本质是最速降线,请看3B1B的视频:[视频链接](https://www.bilibili.com/video/av6385842)<br />另一个相关视频:[费马小定理](https://www.bilibili.com/video/av4283063)<br />**极坐标:**<br />极坐标求面积公式前面已给出:<br />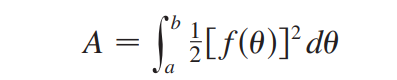<br />求弧长的公式推导依然是微元法:<br />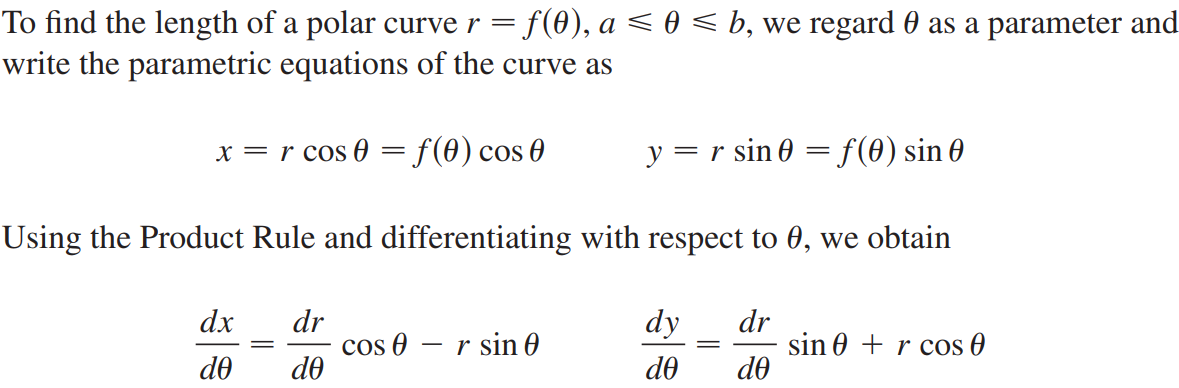<br /><br />更直观的方法是:弧长显然等于径向速度与法向速度之和。$\Delta l=\sqrt{(dr)^2+(rd\theta)^2}$<br />_**Example10:**_<br />
|
||||
|
||||
_**Example11:**_<br />本题请务必自己手算一遍。<br />_****_<br />_****_
|
||||
<a name="hn04R"></a>
|
||||
## 6.2物理问题
|
||||
<a name="q6lMd"></a>
|
||||
#### 6.2.1质心
|
||||
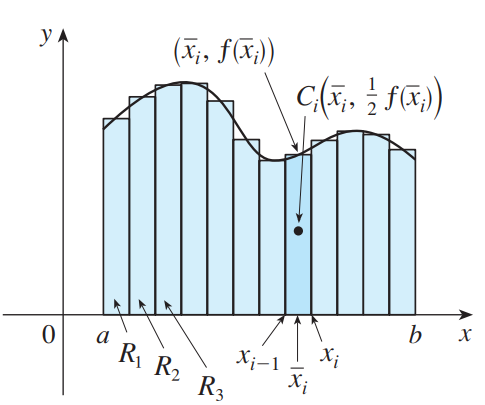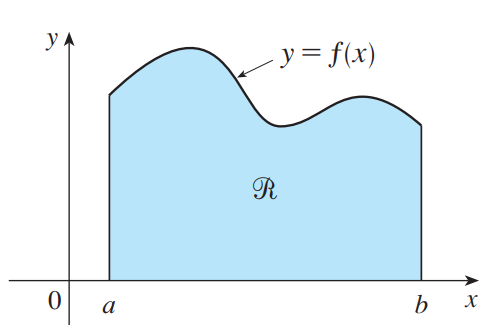<br />质心和势相关,是力学中研究旋转的概念,质心和势一般来说是对于某个转轴的定义。<br />质心是一个点,在这点上施加外力不会引起系统的旋转。<br />势是物体旋转的惯性,表示在施加外力后系统旋转的能力。<br />如上图所示,区域R具有恒定密度,它相对于y轴和x轴的势计算方法如下:<br />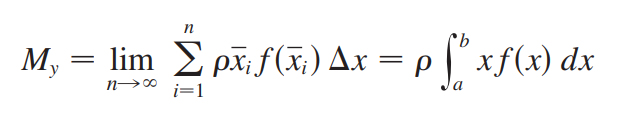(相当于每个矩形到y轴距离x乘以每个矩形面积f(x)dx)<br />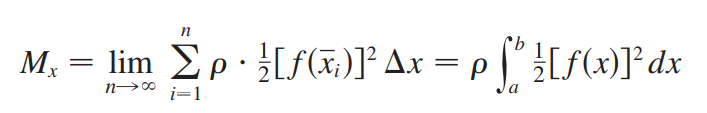(相当于每个矩形中点到x轴距离f(x)/2乘每个矩形面积f(x)dx)<br />上式除以总质量就得到了质心:<br />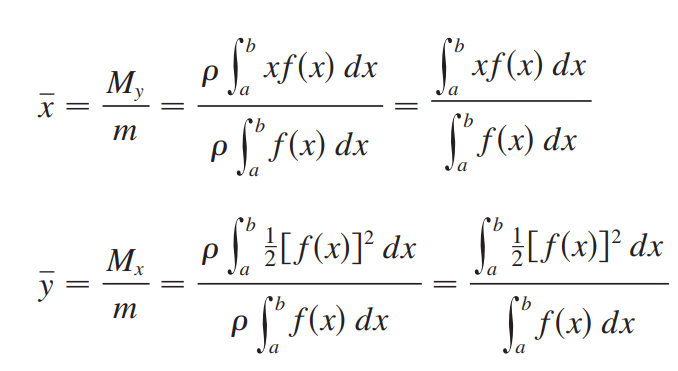<br />_**Example12:**_<br />
|
||||
<a name="yfzzS"></a>
|
||||
#### 6.2.2电磁场
|
||||
_**Example13:**_<br />一根电荷密度为+1的,长度为L的直导体棒,求距离其中点a的一点的电场强度。<br />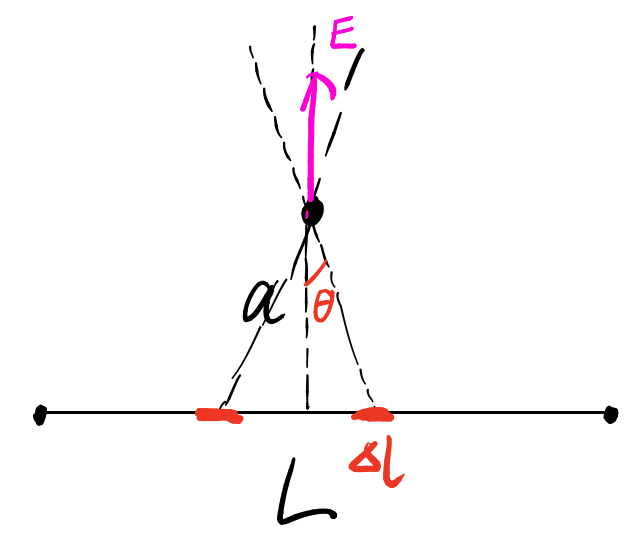<br />提示:第一种做法是通过微元法转换成积分,第二种做法是找出与其等价的圆弧。<br />答案:[点击链接](https://www.bilibili.com/video/av55298726)
|
||||
<a name="CqN2a"></a>
|
||||
## 6.3一题十解
|
||||
_**Example14:**_<br />求$Ax^2+2Bxy+Cy^2=1(A>0,AC-B^2>0)$所围图形的面积。<br />解1:
|
||||
|
||||
<br />另外十种解法为:参数方程,极坐标,微分,二重积分,条件极值,线性代数等,具体参见吉米多维奇。
|
||||
|
||||
|
||||
|
||||
1
8.基础学科/8.基础学科.md
Normal file
1
8.基础学科/8.基础学科.md
Normal file
@@ -0,0 +1 @@
|
||||
# 8. 外行社科
|
||||
Reference in New Issue
Block a user