update

many chore
2023-07-28 23:20:46 +08:00
parent 50c8ebb126
commit 38a91c62e7
13 changed files with 365 additions and 361 deletions
--- a/3.编程思维体系构建/3.4.6.2.探索未知.md
+++ b/3.编程思维体系构建/3.4.6.2.探索未知.md
@@ -128,7 +128,9 @@ bool parseAndExecute(char *input)

 返回<em>false</em>将导致主循环结束。

-RTFM&&STFW 搞懂 strtok 和 strcmp 的用法
+::: warning <font size=5><strong>RTFM&&STFW</strong></font>
+搞懂 strtok 和 strcmp 的用法
+:::

 考虑一下 NULL 是干什么的

--- a/3.编程思维体系构建/3.Y.3Linux初探索.md
+++ b/3.编程思维体系构建/3.Y.3Linux初探索.md
@@ -23,7 +23,7 @@ Linux 命令行中的命令使用格式都是相同的：

 - （重要）首先教一个命令 `sudo su` 进入 root 账户（敲完之后会让你敲当前登录账户的密码 密码敲得过程中没有*****这种传统敲密码的提示 为 linux 传统艺能 其实是敲进去了），因为本身普通账户没什么权限，会出现处处的权限提示，建议直接使用 root 账户。

-```text
+```txt
 这里有一个彩蛋（如果你用的是 centos 的话）
 当用户第一次使用 sudo 权限时 CentOS 的系统提示：
 我们信任您已经从系统管理员那里了解了日常注意事项。
--- a/4.人工智能/4.1前言.md
+++ b/4.人工智能/4.1前言.md
@@ -1,15 +1,14 @@
 # 对 AI 大致方向的概述

-
-# 前言
+## 前言

 在这个时代，相关内容是非常泛滥的，我们在本章内容中，大致的写一些目前比较有名的方向以及它的简介（也许会比 wiki 和百度有趣一点？）

-# 深度学习 的大致方向分类
+## 深度学习 的大致方向分类

 本模块会粗略地介绍目前审读学习的研究与应用领域，在这里提前说明：笔者也只是一名普通的杭电学生，视野与认知有限，某些领域我们了解较多就会介绍地更加详细，某些领域了解较少或笔者中无人从事相关研究，就难免会简略介绍甚至有所偏颇，欢迎大家的指正。

-## CV(计算机视觉)
+### CV(计算机视觉)

 计算机视觉旨在<strong>用计算机模拟人类处理图片信息的能力</strong>，就比如这里有一张图片——手写数字 9

@@ -19,31 +18,39 @@

 相信你通过上面简单的介绍应该能够了解到计算机视觉是在干嘛了，接下来我会举几个相对复杂的例子来让大家了解一下目前的 cv 是在做怎样的研究：

-<strong>图像分割</strong>是在图片中对物体分类，并且把它们所对应的位置标示出来。下图就是把人的五官，面部皮肤和头发分割出来，效(小)果(丑)图如下：
+::: warning 🐱 <strong>图像分割</strong>是在图片中对物体分类，并且把它们所对应的位置标示出来。下图就是把人的五官，面部皮肤和头发分割出来，效 (小) 果 (丑) 图如下：
+:::

-![](https://cdn.xyxsw.site/boxcnxn5GlJZmsrMV5qKNwMlDPc.jpg)
+<table>
+    <tr>
+        <td><img src=https://cdn.xyxsw.site/boxcnxn5GlJZmsrMV5qKNwMlDPc.jpg width=175></td>
+        <td><img src=https://cdn.xyxsw.site/boxcnokdWGegr2XCi1vfg0ZZiWg.png width=200></td>
+        <td><img src=https://cdn.xyxsw.site/boxcn2o9ilOZg6jI6ssTYWhoeme.png width=200></td>
+    </tr>
+</table>

-![](https://cdn.xyxsw.site/boxcnokdWGegr2XCi1vfg0ZZiWg.png)
-
-![](https://cdn.xyxsw.site/boxcn2o9ilOZg6jI6ssTYWhoeme.png)
-
-<strong>图像生成</strong>相信大家一定不陌生，NovalAI 在 2022 年火的一塌糊涂，我觉得不需要我过多赘述，对它(Diffusion model)的改进工作也是层出不穷，这里就放一张由可控姿势网络(ControlNet)生成的图片吧：
+::: warning 🐱 <strong>图像生成</strong>相信大家一定不陌生，NovalAI 在 2022 年火的一塌糊涂，我觉得不需要我过多赘述，对它 (Diffusion model) 的改进工作也是层出不穷，这里就放一张由可控姿势网络 (ControlNet) 生成的图片吧：
+:::

 ![](https://cdn.xyxsw.site/boxcnUjnRociXua1yKj6dmU1A3c.png)

-<strong>三维重建</strong>也是很多研究者关注的方向，指的是传入对同一物体不同视角的照片，来生成 3D 建模的任务。这方面比图像处理更加前沿并且难度更大。具体见[4.6.5.4神经辐射场(NeRF)](4.6.5.4%E7%A5%9E%E7%BB%8F%E8%BE%90%E5%B0%84%E5%9C%BA(NeRF).md) 章节。
+::: warning 🐱 <strong>三维重建</strong>也是很多研究者关注的方向，指的是传入对同一物体不同视角的照片，来生成 3D 建模的任务。这方面比图像处理更加前沿并且难度更大。具体见[4.6.5.4 神经辐射场 (NeRF)](4.6.5.4%E7%A5%9E%E7%BB%8F%E8%BE%90%E5%B0%84%E5%9C%BA(NeRF).md) 章节。
+:::

 如果对计算机视觉有兴趣，可以通过以下路线进行学习：深度学习快速入门—> 经典网络。本块内容的主要撰写者之一<strong>SRT 社团</strong>多数成员主要从事 CV 方向研究，欢迎与我们交流。

-## NLP(自然语言处理)
+### NLP(自然语言处理)

 这就更好理解了，让计算机能够像人类一样，理解文本中的“真正含义”。在计算机眼中，文本就是单纯的字符串，NLP 的工作就是把字符转换为计算机可理解的数据。举个例子，ChatGPT(或者 New Bing) 都是 NLP 的成果。在过去，NLP 领域被细分为了多个小任务，比如文本情感分析、关键段落提取等。而 ChatGPT 的出现可以说是集几乎所有小任务于大成，接下来 NLP 方向的工作会向 ChatGPT 的方向靠近。

-![](https://cdn.xyxsw.site/boxcnyh6pakAkcxCKq6pLylSdef.png)
+<table>
+    <tr>
+        <td><img src=https://cdn.xyxsw.site/boxcnyh6pakAkcxCKq6pLylSdef.png width=580></td>
+        <td><img src=https://cdn.xyxsw.site/boxcnwWnoEDulgWdqGkY0WeYogc.png width=200></td>
+    </tr>
+</table>

-![](https://cdn.xyxsw.site/boxcnwWnoEDulgWdqGkY0WeYogc.png)
-
-## 多模态(跨越模态的处理)
+### 多模态 (跨越模态的处理)

 模态，可以简单理解为数据形式，比如图片是一种模态，文本是一种模态，声音是一种模态，等等……

@@ -55,11 +62,11 @@

 ![](https://cdn.xyxsw.site/boxcnrMvM1THshjXXOuh8WXi2zr.jpg)

-## 对比学习
+### 对比学习

 因为传统 AI 训练一般都需要数据集标注，比如说图片分割数据集需要人工在数万张图片上抠出具体位置，才能进行训练，这样的人力成本是巨大的，而且难以得到更多数据。因此，对比学习应运而生，这是一种不需要进行标注或者只需要少量标注的训练方式，具体可见[4.6.8 对比学习](4.6.8%E5%AF%B9%E6%AF%94%E5%AD%A6%E4%B9%A0.md) 。

-## 强化学习
+### 强化学习

 强调模型如何依据环境（比如扫地机器人在学习家里的陈设，这时陈设就是环境）的变化而改进，以取得最大的收益（比如游戏得到最高分）。

@@ -67,27 +74,26 @@

 强化学习主要理论来源于心理学中的动物学习和最优控制的控制理论。说的通俗点，强化学习就是操控智能体与环境交互、去不断试错，在这个过程中进行学习。因此，强化学习被普遍地应用于游戏、资源优化分配、机器人等领域。强化学习本身已经是个老东西了，但是和深度学习结合之后焕发出了第二春——深度强化学习（DRL）。

-深度强化学习最初来源是2013年谷歌DeepMind团队发表的《Playing Atari with Deep Reinforcement Learning》一文，正式提出Deep Q-network（DQN）算法。在这篇论文中，DeepMind团队训练智能体Agent玩雅达利游戏，并取得了惊人的成绩。事实上，深度强化学习最为人熟知的成就是AlphaGO Zero,它没有使用任何人类棋谱进行训练，训练了三天的成就就已经超过了人类几千年的经验积累<del>导致柯洁道心破碎</del>。
+深度强化学习最初来源是 2013 年谷歌 DeepMind 团队发表的《Playing Atari with Deep Reinforcement Learning》一文，正式提出 Deep Q-network（DQN）算法。在这篇论文中，DeepMind 团队训练智能体 Agent 玩雅达利游戏，并取得了惊人的成绩。事实上，深度强化学习最为人熟知的成就是 AlphaGO Zero，它没有使用任何人类棋谱进行训练，训练了三天的成就就已经超过了人类几千年的经验积累<del>导致柯洁道心破碎</del>。

-# 交叉学科&经典机器学习算法
+## 交叉学科&经典机器学习算法

 交叉学科巨大的难度在于你往往需要掌握多个学科以及其相对应的知识。

 举个例子：如果你想要做出一个可以识别病人是否得了某种疾病，现在你得到了一批数据，你首先得自己可以标注出或者找到这个数据中，哪些是有问题的，并且可以指明问题在哪，如果你想分出更具体的，比如具体哪里有问题，那你可能甚至需要熟悉他并且把他标注出来。

-目前其实全学科都有向着AI走的趋势，例如量化金融，医疗，生物科学（nature的那篇有关氨基酸的重大发现真的很cool)。他们很多都在用非常传统的机器学习算法，甚至有的大公司的算法岗在处理某些数据的时候，可能会先考虑用最简单的决策树试一试
+目前其实全学科都有向着 AI 走的趋势，例如量化金融，医疗，生物科学 (nature 的那篇有关氨基酸的重大发现真的很 cool)。他们很多都在用非常传统的机器学习算法，甚至有的大公司的算法岗在处理某些数据的时候，可能会先考虑用最简单的决策树试一试

-当然，在大语言模型出现的趋势下，很多学科的应用会被融合会被简化会被大一统(科研人的崇高理想），但是不得不提的是，传统的机器学习算法和模型仍然希望你能去了解甚至更进一步学习。
+当然，在大语言模型出现的趋势下，很多学科的应用会被融合会被简化会被大一统 (科研人的崇高理想)，但是不得不提的是，传统的机器学习算法和模型仍然希望你能去了解甚至更进一步学习。

 除了能让你了解所谓前人的智慧，还可以给你带来更进一步的在数学思维，算法思维上的提高。

-# And more?
+## And more?

 我们对 AI 的定义如果仅仅只有这些内容，我认为还是太过于狭隘了，我们可以把知识规划，知识表征等等东西都可以将他划入 AI 的定义中去，当然这些还期待着你的进一步探索和思考~

+## 特别致谢

-# 特别致谢
-
-非常荣幸能在本章中得到 IIPL智能信息处理实验室 http://iipl.net.cn 的宝贵贡献，衷心感谢他们的无私支持与帮助！
+非常荣幸能在本章中得到 IIPL 智能信息处理实验室 [http://iipl.net.cn](http://iipl.net.cn) 的宝贵贡献，衷心感谢他们的无私支持与帮助！

 希望加入 IIPL？欢迎移步[SRT 社团介绍](SRT.md)～
--- a/4.人工智能/4.2机器学习（AI）快速入门（quick
+++ b/4.人工智能/4.2机器学习（AI）快速入门（quick
@@ -1,6 +1,6 @@
 # 机器学习（AI）快速入门（quick start）

-本章内容需要你掌握一定的 python 基础知识。
+::: warning 😇 本章内容需要你掌握一定的 python 基础知识。

 如果你想要快速了解机器学习，并且动手尝试去实践他，你可以先阅览本部分内容。

@@ -11,8 +11,9 @@
 当然我需要承认一点，为了让大家都可以看懂，我做了很多抽象，具有了很多例子，某些内容不太准确，这是必然的，最为准确的往往是课本上精确到少一个字都不行的概念，这是难以理解的。

 本篇内容只适合新手理解使用，所以不免会损失一些精度。
+:::

-# 什么是机器学习
+## 什么是机器学习

 这个概念其实不需要那么多杂七杂八的概念去解释。

@@ -22,17 +23,17 @@

 然后你给了他更多信息，比如说国家给出了某些条例，他分析这个条例一出，房价就会降低，他给你了个新的数据。

-因此我们得出一个结论:机器学习 ＝ 泛型算法。
+因此我们得出一个结论：机器学习 ＝ 泛型算法。

 甚至深度学习，也只是机器学习的一部分，不过使用了更多技巧和方法，增大了计算能力罢了。

 ![](https://cdn.xyxsw.site/boxcnbtaUStj8coQiNTmZzfWqNl.png)

-# 两种机器学习算法
+## 两种机器学习算法

 你可以把机器学习算法分为两大类：监督式学习（supervised Learning）和非监督式学习（unsupervised Learning）。要区分两者很简单，但也非常重要。

-## 监督式学习
+### 监督式学习

 你是卖方的，你公司很大，因此你雇了一批新员工来帮忙。

@@ -50,7 +51,7 @@

 这就是监督学习，你有一个参照物可以帮你决策。

-## 无监督学习
+### 无监督学习

 没有答案怎么办？

@@ -78,24 +79,22 @@

 但是「机器在少量样本数据的基础上找出一个公式来解决特定的问题」不是个好名字。所以最后我们用「机器学习」取而代之。而深度学习，则是机器在数据的基础上通过很深的网络（很多的公式）找一个及解决方案来解决问题。

-# 看看 Code
+## 看看 Code

 如果你完全不懂机器学习知识，你可能会用一堆 if else 条件判断语句来判断比如说房价

 ```python
 def estimate_house_sales_price(num_of_bedrooms, sqft, neighborhood):
  price = 0  # In my area, the average house costs $200 per sqft
-	price_per_sqft = 200  
-	if neighborhood == "hipsterton":
+  price_per_sqft = 200  i f neighborhood == "hipsterton":
    # but some areas cost a bit more
-		price_per_sqft = 400
-	elif neighborhood == "skid row":
+    price_per_sqft = 400  elif neighborhood == "skid row":
    # and some areas cost less
    price_per_sqft = 100  # start with a base price estimate based on how big the place is
  price = price_per_sqft * sqft  # now adjust our estimate based on the number of bedrooms
  if num_of_bedrooms == 0:
    # Studio apartments are cheap
-		price = price - 20000
+    price = price — 20000
  else:
    # places with more bedrooms are usually
    # more valuable
@@ -119,7 +118,7 @@ def estimate_house_sales_price(num_of_bedrooms, sqft, neighborhood):

 如果你可以找到这么一个公式：

-Y(房价)=W(参数）*X1（卧室数量）+W*X2（面积）+W*X3（地段）
+Y(房价)=W(参数) \* X1(卧室数量) + W \*X2(面积) + W \* X3(地段)

 你是不是会舒服很多，可以把他想象成，你要做菜，然后那些参数就是佐料的配比

@@ -151,7 +150,7 @@ def estimate_house_sales_price(num_of_bedrooms, sqft, neighborhood):

 第三步：

-通过尝试所有可能的权重值组合，不断重复第二步。哪一个权重组合的代价最接近于 0，你就使用哪个。当你找到了合适的权重值，你就解决了问题!
+通过尝试所有可能的权重值组合，不断重复第二步。哪一个权重组合的代价最接近于 0，你就使用哪个。当你找到了合适的权重值，你就解决了问题！

 兴奋的时刻到了！

@@ -210,7 +209,7 @@ def estimate_house_sales_price(num_of_bedrooms, sqft, neighborhood):

 换言之，尽管基本概念非常简单，要通过机器学习得到有用的结果还是需要一些技巧和经验的。但是，这是每个开发者都能学会的技巧。

-# 更为智能的预测
+## 更为智能的预测

 我们通过上一次的函数假设已经得到了一些值。

@@ -241,7 +240,7 @@ def estimate_house_sales_price(num_of_bedrooms, sqft, neighborhood):

 这样我们相当于得到了更为准确的答案

-# 神经网络是什么
+## 神经网络是什么

 ![](https://cdn.xyxsw.site/boxcnhLjMMdts91f8gcpgSVE8Ed.png)

@@ -299,14 +298,16 @@ y_test=model(x_test)
 print('y_pred=',y_test.data)
 ```

-# 由浅入深（不会涉及代码）
+## 由浅入深（不会涉及代码）

-# 为什么不教我写代码？
+::: warning 😇 为什么不教我写代码？

 因为你可能看这些基础知识感觉很轻松毫无压力，但是倘若附上很多代码，会一瞬间拉高这里的难度，虽然仅仅只是调包。

 但是我还是会在上面贴上一点代码，但不会有很详细的讲解，因为很多都是调包，没什么好说的，如果你完全零基础，忽略这部分内容即可

+:::
+
 我们尝试做一个神奇的工作，那就是用神经网络来识别一下手写数字，听上去非常不可思议，但是我要提前说的一点是，图像也不过是数据的组合，每一张图片有不同程度的像素值，如果我们把每一个像素值都当成神经网络的输入值，然后经过一个黑盒，让他识别出一个他认为可能的数字，然后进行纠正即可。

 机器学习只有在你拥有数据（最好是大量数据）的情况下，才能有效。所以，我们需要有大量的手写「8」来开始我们的尝试。幸运的是，恰好有研究人员建立了 [MNIST 手写数字数据库](https://link.zhihu.com/?target=http%3A//yann.lecun.com/exdb/mnist/)，它能助我们一臂之力。MNIST 提供了 60,000 张手写数字的图片，每张图片分辨率为 18×18。即有这么多的数据。
@@ -345,7 +346,7 @@ model.add(Activation('relu'))# 激活函数，你可以理解为加上这个东

 现在唯一要做的就是用各种「8」和非「8」的图片来训练我们的神经网络了。当我们喂给神经网络一个「8」的时候，我们会告诉它是「8」的概率是 100% ，而不是「8」的概率是 0%，反之亦然。

-# 仅此而已吗
+## 仅此而已吗

 当数字并不是正好在图片中央的时候，我们的识别器就完全不工作了。一点点的位移我们的识别器就掀桌子不干了

@@ -355,7 +356,7 @@ model.add(Activation('relu'))# 激活函数，你可以理解为加上这个东

 在真实世界中，这种识别器好像并没什么卵用。真实世界的问题永远不会如此轻松简单。所以，我们需要知道，当「8」不在图片正中时，怎么才能让我们的神经网络识别它。

-## 暴力方法：更多的数据和更深的网络
+### 暴力方法：更多的数据和更深的网络

 他不能识别靠左靠右的数据？我们都给他！给他任何位置的图片！

@@ -371,7 +372,7 @@ model.add(Activation('relu'))# 激活函数，你可以理解为加上这个东

 一层一层堆叠起来，这种方法很早就出现了。

-## 更好的方法？
+### 更好的方法？

 你可以通过卷积神经网络进行进一步的处理

@@ -389,7 +390,7 @@ model.add(Activation('relu'))# 激活函数，你可以理解为加上这个东

 ![](https://cdn.xyxsw.site/boxcnsm0cJGKqt0AU8Kv3K3rkKg.png)

-## 卷积是如何工作的
+### 卷积是如何工作的

 之前我们提到过，我们可以把一整张图片当做一串数字输入到神经网络里面。不同的是，这次我们会利用<strong>平移不变性</strong>的概念来把这件事做得更智能。

@@ -405,7 +406,7 @@ model.add(Activation('relu'))# 激活函数，你可以理解为加上这个东

 换一句话来说，我们从一整张图片开始，最后得到一个稍小一点的数组，里面存储着我们图片中的哪一部分有异常。

-## 池化层
+### 池化层

 图像可能特别大。比如说 1024*1024 再来个颜色 RGB

@@ -429,7 +430,7 @@ model.add(Activation('relu'))# 激活函数，你可以理解为加上这个东

 我们也要感谢显卡，这项技术早就出现了但是一直算不了，有了显卡让这件事成为了可能。

-## 作出预测
+### 作出预测

 到现在为止，我们已经把一个很大的图片缩减到了一个相对较小的数组。

@@ -445,10 +446,10 @@ model.add(Activation('relu'))# 激活函数，你可以理解为加上这个东

 比如说，第一个卷积的步骤可能就是尝试去识别尖锐的东西，而第二个卷积步骤则是通过找到的尖锐物体来找鸟类的喙，最后一步是通过鸟喙来识别整只鸟，以此类推。

-# 结语
+## 结语

 这篇文章仅仅只是粗略的讲述了一些机器学习的一些基本操作，如果你要更深一步学习的话你可能还需要更多的探索。

-# 参考资料
+## 参考资料

 [machine-learning-for-software-engineers/README-zh-CN.md at master · ZuzooVn/machine-learning-for-sof](https://github.com/ZuzooVn/machine-learning-for-software-engineers/blob/master/README-zh-CN.md#%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0%E6%A6%82%E8%AE%BA)
--- a/4.人工智能/4.3.1.1程序示例——maze迷宫解搜索.md
+++ b/4.人工智能/4.3.1.1程序示例——maze迷宫解搜索.md
@@ -1,4 +1,5 @@
 # 程序示例——maze 迷宫解搜索
+
 ::: warning 😋
 阅读程序中涉及搜索算法的部分，然后运行程序，享受机器自动帮你寻找路径的快乐！
 完成习题
@@ -10,7 +11,7 @@

 /4.人工智能/code/MAZE.zip

-# Node
+## Node

 ```python
 # 节点类 Node
@@ -21,7 +22,7 @@ class Node:
        self.action = action      # 存储采取的行动
 ```

-## 节点复习：
+## 节点复习

 - 节点是一种包含以下数据的数据结构：
  - 状态——state
@@ -29,7 +30,7 @@ class Node:
  - 应用于父级状态以获取当前节点的操作——action
  - 从初始状态到该节点的路径成本——path cost

-# 堆栈边域——DFS
+## 堆栈边域——DFS

 ```python
 class StackFrontier:  # 堆栈边域
@@ -50,11 +51,11 @@ class StackFrontier:  # 堆栈边域
            return node
 ```

-## 深度优先搜索复习：
+## 深度优先搜索复习

 - 深度优先搜索算法在尝试另一个方向之前耗尽每个方向。在这些情况下，边域作为堆栈数据结构进行管理。这里需要记住的流行语是“后进先出”。在将节点添加到边域后，第一个要删除和考虑的节点是最后一个要添加的节点。这导致了一种搜索算法，该算法在第一个方向上尽可能深入，直到尽头，同时将所有其他方向留到后面。“不撞南墙不回头”

-# 队列边域——BFS
+## 队列边域——BFS

 ```python
 class QueueFrontier(StackFrontier):  # 队列边域
@@ -67,11 +68,11 @@ class QueueFrontier(StackFrontier):  # 队列边域
            return node
 ```

-## 广度优先搜索复习：
+## 广度优先搜索复习

 - 广度优先搜索算法将同时遵循多个方向，在每个可能的方向上迈出一步，然后在每个方向上迈出第二步。在这种情况下，边域作为队列数据结构进行管理。这里需要记住的流行语是“先进先出”。在这种情况下，所有新节点都会排成一行，并根据先添加的节点来考虑节点（先到先得！）。这导致搜索算法在任何一个方向上迈出第二步之前，在每个可能的方向上迈出一步。

-# 迷宫解——Maze_solution
+## 迷宫解——Maze_solution

 ```python
 class Maze:
@@ -166,7 +167,7 @@ class Maze:
        ...
 ```

-# Quiz
+## Quiz

 1. 在深度优先搜索（DFS）和广度优先搜索（BFS）之间，哪一个会在迷宫中找到更短的路径？
   1. DFS 将始终找到比 BFS 更短的路径
--- a/4.人工智能/4.3.1.2项目：Tic-Tac-Toe井字棋.md
+++ b/4.人工智能/4.3.1.2项目：Tic-Tac-Toe井字棋.md
@@ -1,8 +1,9 @@
 # 项目：Tic-Tac-Toe 井字棋

-我们为你提供了一个简单有趣的项目，帮助你进行知识巩固，请认真阅读文档内容。
+::: warning 😋 我们为你提供了一个简单有趣的项目，帮助你进行知识巩固，请认真阅读文档内容。

 如果你卡住了，请记得回来阅读文档，或请求身边人的帮助。
+:::

 ::: tip 📥
 本节附件下载 <Download url="https://cdn.xyxsw.site/code/1-Projects.zip"/>
@@ -10,13 +11,13 @@

 `pip3 install -r requirements.txt`

-# 理解
+## 理解

 - 这个项目有两个主要文件：`runner.py` 和 `tictactoe.py`。`tictactoe.py` 包含了玩游戏和做出最佳动作的所有逻辑。`runner.py` 已经为你实现，它包含了运行游戏图形界面的所有代码。一旦你完成了 `tictactoe.py` 中所有必需的功能，你就可以运行 `python runner.py` 来对抗你的人工智能了！
 - 让我们打开 `tictactoe.py` 来了解所提供的内容。首先，我们定义了三个变量：X、O 和 EMPTY，以表示游戏的可能移动。
 - 函数 `initial_state` 返回游戏的启动状态。对于这个问题，我们选择将游戏状态表示为三个列表的列表（表示棋盘的三行），其中每个内部列表包含三个值，即 X、O 或 EMPTY。以下是我们留给你实现的功能！

-# 说明
+## 说明

 - 实现 `player`, `actions`, `result`, `winner`, `terminal`, `utility`, 以及 `minimax`.

@@ -55,7 +56,7 @@
  - 对于所有接受棋盘作为输入的函数，你可以假设它是一个有效的棋盘（即，它是包含三行的列表，每行都有三个值 X、O 或 EMPTY）。你不应该修改所提供的函数声明（每个函数的参数的顺序或数量）。、
  - 一旦所有功能都得到了正确的实现，你就应该能够运行 `python runner.py` 并与你的人工智能进行比赛。而且，由于井字棋是双方最佳比赛的平局，你永远不应该能够击败人工智能（尽管如果你打得不好，它可能会打败你！）

-# 提示
+## 提示

 - 如果你想在不同的 Python 文件中测试你的函数，你可以用类似于 `from tictactoe import initial_state` 的代码来导入它们。
 - 欢迎在 `tictactoe.py` 中添加其他辅助函数，前提是它们的名称不会与模块中已有的函数或变量名称冲突。
--- a/4.人工智能/4.3.1搜索.md
+++ b/4.人工智能/4.3.1搜索.md
@@ -1,16 +1,18 @@
 # 搜索

-在我们日常生活中，其实有非常多的地方使用了所谓的 AI 算法，只是我们通常没有察觉。
+::: warning 😅 在我们日常生活中，其实有非常多的地方使用了所谓的 AI 算法，只是我们通常没有察觉。

 比如美团的外卖程序里面，可以看到外卖员到达你所在的位置的路线，它是如何规划出相关路线的呢？

 在我们和电脑下围棋下五子棋的时候，他是如何“思考”的呢？希望你在阅读完本章内容之后，可以有一个最基本的理解。并且，我们还会给你留下一个井字棋的小任务，可以让你的电脑和你下井字棋，是不是很 cool

 让我们现在开始吧！
+:::

-# 基本定义
+## 基本定义

-也许第一次看会觉得云里雾里，没有必要全部记住所有的概念。可以先大致浏览一遍之后，再后续的代码中与概念进行结合，相信你会有更深入的理解
+::: warning 🤔 也许第一次看会觉得云里雾里，没有必要全部记住所有的概念。可以先大致浏览一遍之后，再后续的代码中与概念进行结合，相信你会有更深入的理解
+:::

 > 即检索存储在某个[数据结构](https://zh.wikipedia.org/wiki/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84)中的信息，或者在问题域的搜索空间中计算的信息。 --wiki

@@ -26,7 +28,7 @@

 ![](https://cdn.xyxsw.site/LPgEbVQg2oZBSexmGWwcwfbdnVd.png)

-# 举个例子
+## 举个例子

 要找到一个数字华容道谜题的解决方案，需要使用搜索算法。

@@ -74,7 +76,7 @@

  - 完成给定路径相关的代价。例如，导航应用程序并不是简单地让你达到目标；它这样做的同时最大限度地减少了路径成本，为您找到了达到目标状态的最快方法。

-# 解决搜索问题
+## 解决搜索问题

 - 解 (solution)

@@ -128,7 +130,7 @@ c. 到达目标节点，停止，返回解决方案

 会出现什么问题？节点 A-> 节点 B-> 节点 A->......-> 节点 A。我们需要一个探索集，记录已搜索的节点！

-## 不知情搜索(Uninformed Search)
+### 不知情搜索 (Uninformed Search)

 - 在之前对边域的描述中，有一件事没有被提及。在上面伪代码的第 1 阶段，应该删除哪个节点？这种选择对解决方案的质量和实现速度有影响。关于应该首先考虑哪些节点的问题，有多种方法，其中两种可以用堆栈（深度优先搜索）和队列（广度优先搜索）的数据结构来表示。
 - 深度优先搜索 (Depth-First Search)
@@ -201,7 +203,6 @@ def remove(self):
 - 贪婪最佳优先搜索 (Greedy Best-First Search)

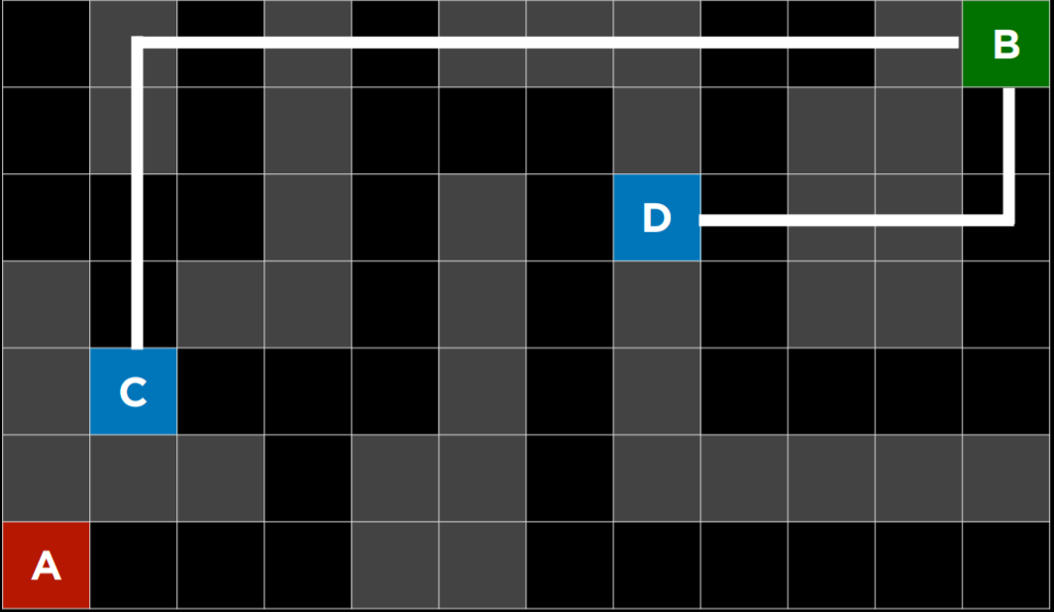
  - 贪婪最佳优先搜索扩展最接近目标的节点，如启发式函数$h(n)$所确定的。顾名思义，该函数估计下一个节点离目标有多近，但可能会出错。贪婪最佳优先算法的效率取决于启发式函数的好坏。例如，在迷宫中，算法可以使用启发式函数，该函数依赖于可能节点和迷宫末端之间的曼哈顿距离。曼哈顿距离忽略了墙壁，并计算了从一个位置到目标位置需要向上、向下或向两侧走多少步。这是一个简单的估计，可以基于当前位置和目标位置的$(x，y)$坐标导出。
-
 ![](https://cdn.xyxsw.site/Pe3WbBuTjomWjfxd5Ryc3OPPnSd.png)

  - 然而，重要的是要强调，与任何启发式算法一样，它可能会出错，并导致算法走上比其他情况下更慢的道路。不知情的搜索算法有可能更快地提供一个更好的解决方案，但它比知情算法更不可能这样。
@@ -212,19 +213,19 @@ def remove(self):

 - $A^*$搜索
  
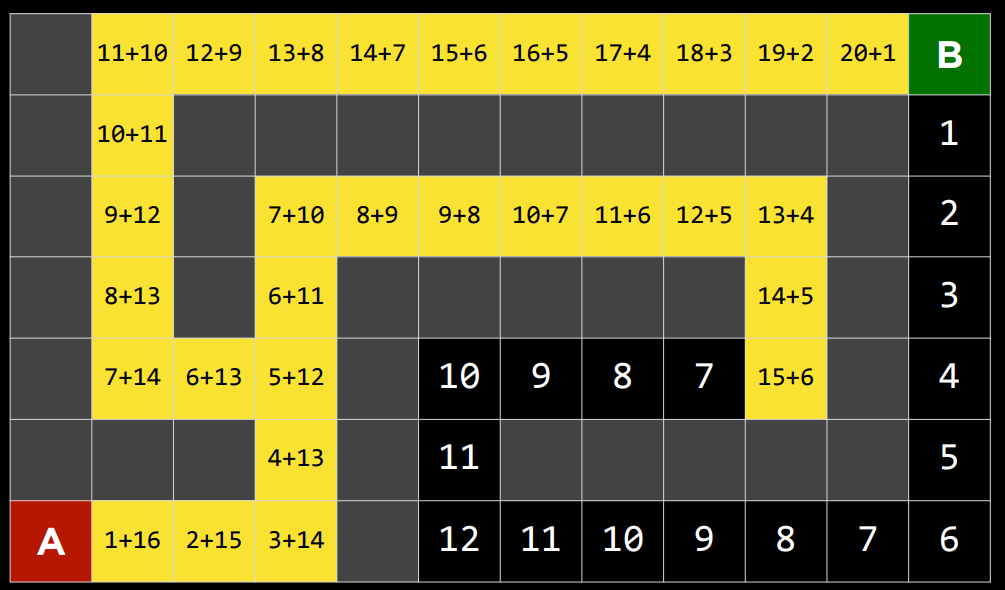
-  - 作为贪婪最佳优先算法的一种发展，$A^*$搜索不仅考虑了从当前位置到目标的估计成本$h(n)$，还考虑了直到当前位置为止累积的成本$g(n)$。通过组合这两个值，该算法可以更准确地确定解决方案的成本并在旅途中优化其选择。该算法跟踪（到目前为止的路径成本+到目标的估计成本,$g(n)+h(n)$），一旦它超过了之前某个选项的估计成本，该算法将放弃当前路径并返回到之前的选项，从而防止自己沿着$h(n)$错误地标记为最佳的却长而低效的路径前进。
+  - 作为贪婪最佳优先算法的一种发展，$A^*$搜索不仅考虑了从当前位置到目标的估计成本$h(n)$，还考虑了直到当前位置为止累积的成本$g(n)$。通过组合这两个值，该算法可以更准确地确定解决方案的成本并在旅途中优化其选择。该算法跟踪（到目前为止的路径成本 + 到目标的估计成本，$g(n)+h(n)$），一旦它超过了之前某个选项的估计成本，该算法将放弃当前路径并返回到之前的选项，从而防止自己沿着$h(n)$错误地标记为最佳的却长而低效的路径前进。
  
  - 然而，由于这种算法也依赖于启发式，所以它依赖它所使用的启发式。在某些情况下，它可能比贪婪的最佳第一搜索甚至不知情的算法效率更低。对于最佳的$A^*$搜索，启发式函数$h(n)$应该：

    - 可接受，从未高估真实成本。

-    - 一致性，这意味着从新节点到目标的估计路径成本加上从先前节点转换到该新节点的成本应该大于或等于先前节点到目标的估计路径成本。用方程的形式表示，$h(n)$是一致的，如果对于每个节点n$和后续节点n'$，从n$到$n'$的步长为c$，满足$h(n)≤h(n')+c$。
+    - 一致性，这意味着从新节点到目标的估计路径成本加上从先前节点转换到该新节点的成本应该大于或等于先前节点到目标的估计路径成本。用方程的形式表示，$h(n)$是一致的，如果对于每个节点 n$和后续节点 n'$,从 n$到$n'$的步长为 c$,满足$h(n) ≤ h(n') + c$.

 ![](https://cdn.xyxsw.site/BbIiba1pwo3uI7x4k7QcwicznGc.png)

 ![](https://cdn.xyxsw.site/HhG9bcJP2okKMMxY0FGclP0AnXY.png)

-# 对抗性搜索
+## 对抗性搜索

 尽管之前我们讨论过需要找到问题答案的算法，但在对抗性搜索中，算法面对的是试图实现相反目标的对手。通常，在游戏中会遇到使用对抗性搜索的人工智能，比如井字游戏。

@@ -258,14 +259,11 @@ def remove(self):

    - $Utility(s)$: 一个函数，在给定终端状态 s 的情况下，返回状态的效用值：$$-1、0 或 1$$。

-      
-
 ![](https://cdn.xyxsw.site/UcpAbpWtJoHb5Wx6ycrcG2ZZnIe.png)

 - 算法的工作原理：

  - 该算法递归地模拟从当前状态开始直到达到终端状态为止可能发生的所有游戏状态。每个终端状态的值为$(-1)$、$0$或$(+1)$。
-
 ![](https://cdn.xyxsw.site/DN3mb0lbno2AHvx2M0JcrTvtnYf.png)

  - 根据轮到谁的状态，算法可以知道当前玩家在最佳游戏时是否会选择导致状态值更低或更高的动作。
@@ -302,7 +300,7 @@ def remove(self):
      - $$v = Min(v, Max-Value(Result(state, action)))$$
    - return $v$

-不会理解递归？也许你需要看看这个：[阶段二:递归操作](../3.%E7%BC%96%E7%A8%8B%E6%80%9D%E7%BB%B4%E4%BD%93%E7%B3%BB%E6%9E%84%E5%BB%BA/3.6.4.2%E9%98%B6%E6%AE%B5%E4%BA%8C%EF%BC%9A%E9%80%92%E5%BD%92%E6%93%8D%E4%BD%9C.md)
+不会理解递归？也许你需要看看这个：[阶段二：递归操作](../3.%E7%BC%96%E7%A8%8B%E6%80%9D%E7%BB%B4%E4%BD%93%E7%B3%BB%E6%9E%84%E5%BB%BA/3.6.4.2%E9%98%B6%E6%AE%B5%E4%BA%8C%EF%BC%9A%E9%80%92%E5%BD%92%E6%93%8D%E4%BD%9C.md)

 - $\alpha$-$\beta$剪枝 (Alpha-Beta Pruning)

--- a/4.人工智能/4.3.2.1程序示例——命题逻辑与模型检测.md
+++ b/4.人工智能/4.3.2.1程序示例——命题逻辑与模型检测.md
@@ -1,4 +1,5 @@
 # 程序示例——命题逻辑与模型检测
+
 ::: warning 😋
 阅读程序中涉及命题逻辑的部分，然后“玩一玩”程序！

@@ -8,7 +9,8 @@
 ::: tip 📥
 本节附件下载 <Download url="https://cdn.xyxsw.site/code/2-Lecture.zip"/>
 :::
-# Sentence——父类
+
+## Sentence——父类

 ```python
 class Sentence(): # 父类
@@ -46,7 +48,7 @@ class Sentence(): # 父类
            return f"({s})"
 ```

-# Symbol——命题符号类
+## Symbol——命题符号类

 ```python
 class Symbol(Sentence):
@@ -71,7 +73,7 @@ class Symbol(Sentence):
        return {self.name}
 ```

-# Not——逻辑非类
+## Not——逻辑非类

 ```python
 class Not(Sentence):
@@ -94,7 +96,7 @@ class Not(Sentence):
        return self.operand.symbols()
 ```

-# And——逻辑乘类
+## And——逻辑乘类

 ```python
 class And(Sentence):
@@ -124,7 +126,7 @@ class And(Sentence):
        return set.union(*[conjunct.symbols() for conjunct in self.conjuncts])
 ```

-# Or——逻辑和类
+## Or——逻辑和类

 ```python
 class Or(Sentence):
@@ -151,7 +153,7 @@ class Or(Sentence):
        return set.union(*[disjunct.symbols() for disjunct in self.disjuncts])
 ```

-# Implication——逻辑蕴含类
+## Implication——逻辑蕴含类

 ```python
 class Implication(Sentence):
@@ -183,7 +185,7 @@ class Implication(Sentence):
        return set.union(self.antecedent.symbols(), self.consequent.symbols())
 ```

-# Biconditional——逻辑等值类
+## Biconditional——逻辑等值类

 ```python
 class Biconditional(Sentence):
@@ -215,7 +217,7 @@ class Biconditional(Sentence):
        return set.union(self.left.symbols(), self.right.symbols())
 ```

-# Model_check()——模型检测算法
+## Model_check()——模型检测算法

 ```python
 def model_check(knowledge, query):
@@ -259,7 +261,7 @@ def model_check(knowledge, query):
    return check_all(knowledge, query, symbols, dict())
 ```

-# 线索游戏
+## 线索游戏

 在游戏中，一个人在某个地点使用工具实施了谋杀。人、工具和地点用卡片表示。每个类别的一张卡片被随机挑选出来，放在一个信封里，由参与者来揭开真相。参与者通过揭开卡片并从这些线索中推断出信封里必须有什么来做到这一点。我们将使用之前的模型检查算法来揭开这个谜团。在我们的模型中，我们将已知与谋杀有关的项目标记为 True，否则标记为 False。

@@ -311,7 +313,7 @@ knowledge.add(Not(ballroom))
 check_knowledge(knowledge)
 ```

-# Mastermind 游戏
+## Mastermind 游戏

 在这个游戏中，玩家一按照一定的顺序排列颜色，然后玩家二必须猜测这个顺序。每一轮，玩家二进行猜测，玩家一返回一个数字，指示玩家二正确选择了多少颜色。让我们用四种颜色模拟一个游戏。假设玩家二猜测以下顺序：

@@ -379,7 +381,7 @@ for symbol in symbols:
        print(symbol)
 ```

-# Quiz
+## Quiz

 1. 下面的问题将问你关于以下逻辑句子的问题。1.如果 Hermione 在图书馆，那么 Harry 在图书馆。2.Hermione 在图书馆里。3.Ron 在图书馆，Ron 不在图书馆。4.Harry 在图书馆。5.Harry 不在图书馆，或者 Hermione 在图书馆。6.Rom 在图书馆，或者 Hermione 在图书馆。

--- a/4.人工智能/4.3.2.2项目：扫雷，骑士与流氓问题.md
+++ b/4.人工智能/4.3.2.2项目：扫雷，骑士与流氓问题.md
@@ -1,8 +1,9 @@
 # 项目：扫雷，骑士与流氓问题

-我们为你提供了两个简单有趣的项目，帮助你进行知识巩固，请认真阅读文档内容。
+::: warning 😋 我们为你提供了两个简单有趣的项目，帮助你进行知识巩固，请认真阅读文档内容。

 如果你卡住了，请记得回来阅读文档，或请求身边人的帮助。
+:::

 ::: tip 📥
 本节附件下载 <Download url="https://cdn.xyxsw.site/code/2-Projects.zip"/>
@@ -10,9 +11,9 @@

 `pip3 install -r requirements.txt`

-# 骑士与流氓问题
+## 骑士与流氓问题

-## 背景
+### 背景

 - 在 1978 年，逻辑学家雷蒙德·斯穆里安（Raymond Smullyan）出版了《这本书叫什么名字？》，这是一本逻辑难题的书。在书中的谜题中，有一类谜题被斯穆里安称为“骑士与流氓”谜题。
 - 在骑士与流氓谜题中，给出了以下信息：每个角色要么是骑士，要么是流氓。骑士总是会说实话：如果骑士陈述了一句话，那么这句话就是真的。相反，流氓总是说谎：如果流氓陈述了一个句子，那么这个句子就是假的。
@@ -21,7 +22,7 @@
 - 从逻辑上讲，我们可以推断，如果 A 是骑士，那么这句话一定是真的。但我们知道这句话不可能是真的，因为 A 不可能既是骑士又是流氓——我们知道每个角色要么是骑士，要么是流氓，不会出现是流氓的骑士或是骑士的流氓。所以，我们可以得出结论，A 一定是流氓。
 - 那个谜题比较简单。随着更多的字符和更多的句子，谜题可以变得更加棘手！你在这个问题中的任务是确定如何使用命题逻辑来表示这些谜题，这样一个运行模型检查算法的人工智能可以为我们解决这些谜题。

-## 理解
+### 理解

 - 看一下 `logic.py`，你可能还记得讲义的内容。无需了解此文件中的所有内容，但请注意，此文件为不同类型的逻辑连接词定义了多个类。这些类可以相互组合，所以表达式 `And(Not(A), Or(B, C))` 代表逻辑语句：命题 A 是不正确的，同时，命题 B 或者命题 C 是正确的。（这里的“或”是同或，不是异或）
 - 回想一下 `logic.py`，它还包含一个 函数 `model_check` 。`model_check` 输入知识库和查询结论。知识库是一个逻辑命题：如果知道多个逻辑语句，则可以将它们连接在一个表达式中。递归考虑所有可能的模型，如果知识库推理蕴含查询结论，则返回 `True`，否则返回 `False`。
@@ -29,7 +30,7 @@
 - 接下来是四个不同的知识库 `knowledge0`, `knowledge1`, `knowledge2`, and `knowledge3`，它们将分别包含推断即将到来的谜题 0、1、2 和 3 的解决方案所需的知识。请注意，目前，这些知识库中的每一个都是空的。这就是你进来的地方！
 - 这个 `puzzle.py` 的 `main` 函数在所有谜题上循环，并使用模型检查来计算，给定谜题的知识，无论每个角色是骑士还是无赖，打印出模型检查算法能够得出的任何结论。

-## 明确
+### 明确

 - 将知识添加到知识库 `knowledge0`, `knowledge1`, `knowledge2`, 和 `knowledge3` 中，以解决以下难题。

@@ -62,7 +63,7 @@ C 说：“A 是骑士。”
 - 上述每个谜题中，每个角色要么是骑士，要么是流氓。骑士说的每一句话都是真的，流氓说的每一句话都是假的。
 - 一旦你完成了一个问题的知识库，你应该能够运行 `python puzzle.py` 来查看谜题的解决方案。

-## 提示
+### 提示

 - 对于每个知识库，你可能想要编码两种不同类型的信息：（1）关于问题本身结构的信息（即骑士与流氓谜题定义中给出的信息），以及（2）关于角色实际说了什么的信息。
 - 考虑一下，如果一个句子是由一个角色说出的，这意味着什么。在什么条件下这句话是真的？在什么条件下这个句子是假的？你如何将其表达为一个合乎逻辑的句子？
@@ -71,15 +72,15 @@ C 说：“A 是骑士。”
  - 例如，对于谜题 0，设置 `knowledge0=AKnave` 将产生正确的输出，因为通过我们自己的推理，我们知道 A 一定是一个无赖。但这样做违背了这个问题的精神：目标是让你的人工智能为你做推理。
 - 您不需要（也不应该）修改 `logic.py` 来完成这个问题。

-# 扫雷
+## 扫雷

 写一个 AI 来玩扫雷游戏。

 ![](https://cdn.xyxsw.site/CQmGb6QTjoeyVCx9vjncYF2QnQe.png)

-## 背景
+### 背景

-### 扫雷
+#### 扫雷游戏

 - 扫雷器是一款益智游戏，由一个单元格网格组成，其中一些单元格包含隐藏的“地雷”。点击包含地雷的单元格会引爆地雷，导致用户输掉游戏。单击“安全”单元格（即不包含地雷的单元格）会显示一个数字，指示有多少相邻单元格包含地雷，其中相邻单元格是指从给定单元格向左、向右、向上、向下或对角线一个正方形的单元格。
 - 例如，在这个 3x3 扫雷游戏中，三个 1 值表示这些单元格中的每个单元格都有一个相邻的单元格，该单元格是地雷。四个 0 值表示这些单元中的每一个都没有相邻的地雷。
@@ -89,7 +90,7 @@ C 说：“A 是骑士。”
 - 给定这些信息，玩家根据逻辑可以得出结论，右下角单元格中一定有地雷，左上角单元格中没有地雷，因为只有在这种情况下，其他单元格上的数字标签才会准确。
 - 游戏的目标是标记（即识别）每个地雷。在游戏的许多实现中，包括本项目中的实现中，玩家可以通过右键单击单元格（或左键双击，具体取决于计算机）来标记地雷。

-### 命题逻辑
+#### 命题逻辑

 - 你在这个项目中的目标是建立一个可以玩扫雷游戏的人工智能。回想一下，基于知识的智能主体通过考虑他们的知识库来做出决策，并根据这些知识做出推断。
 - 我们可以表示人工智能关于扫雷游戏的知识的一种方法是，使每个单元格成为命题变量，如果单元格包含地雷，则为真，否则为假。
@@ -100,7 +101,7 @@ C 说：“A 是骑士。”
 - `Or(A,B,C,D,E,F,G,H)`
 - 但事实上，我们知道的比这个表达所说的要多。上面的逻辑命题表达了这样一种观点，即这八个变量中至少有一个是真的。但我们可以做一个更有力的陈述：我们知道八个变量中有一个是真的。这给了我们一个命题逻辑命题，如下所示。

-```
+```txt
 Or(
    And(A, Not(B), Not(C), Not(D), Not(E), Not(F), Not(G), Not(H)),
    And(Not(A), B, Not(C), Not(D), Not(E), Not(F), Not(G), Not(H)),
@@ -121,7 +122,7 @@ Or(

  个可能的模型——太多了，计算机无法在任何合理的时间内计算。对于这个问题，我们需要更好地表达知识。

-### 知识表示
+#### 知识表示

 - 相反，我们将像下面这样表示人工智能知识的每一句话。
 - `{A, B, C, D, E, F, G, H} = 1`
@@ -147,7 +148,7 @@ Or(
 - 更一般地说，任何时候我们有两个命题满足 `set1=count1` 和 `set2=count2`，其中 `set1` 是 `set2` 的子集，那么我们可以构造新的命题 `set2-set1=count2-count1`。考虑上面的例子，以确保你理解为什么这是真的。
 - 因此，使用这种表示知识的方法，我们可以编写一个人工智能智能主体，它可以收集有关扫雷的知识，并希望选择它知道安全的单元格！

-## 理解
+### 理解

 - 这个项目有两个主要文件：`runner.py` 和 `minesweeper.py`。`minesweeper.py` 包含游戏本身和 AI 玩游戏的所有逻辑。`runner.py` 已经为你实现，它包含了运行游戏图形界面的所有代码。一旦你完成了 `minesweeper.py` 中所有必需的功能，你就可以运行 `python runner.py` 来玩扫雷了（或者让你的 AI 为你玩）！
 - 让我们打开 `minesweeper.py` 来了解提供了什么。这个文件中定义了三个类，`Minesweeper`，负责处理游戏；`Sentence`，表示一个既包含一组 `cell` 又包含一个 `count` 的逻辑命题；以及 `MinesweeperAI`，它处理根据知识做出的推断。
@@ -157,7 +158,7 @@ Or(
 - `mark_mine` 函数为 `self.mines` 添加了一个单元格，因此 AI 知道这是一个地雷。它还循环遍历人工智能知识中的所有命题，并通知每个命题该单元格是地雷，这样，如果命题包含有关地雷的信息，它就可以相应地更新自己。`mark_safe` 函数也做同样的事情，只是针对安全单元格。
 - 剩下的函数 `add_knowledge`、`make_safe_move` 和 `make_random_move` 由你完成！

-## 明确
+### 明确

 - 完成 `minesweeper.py` 中的 `Sentence` 类和 `MinesweeperAI` 类的实现。
 - 在 `Sentence` 类中，完成 `known_mines`、`known_safes`、`mark_mine` 和 `mark_safe` 的实现。
@@ -194,11 +195,11 @@ Or(
  - 此举决不能是已知的地雷行动。
  - 如果无法进行此类移动，则函数应返回 `None`。

-## 提示
+### 提示

 - 确保你已经彻底阅读了背景部分，以了解知识在这个人工智能中是如何表现的，以及人工智能是如何进行推理的。
- 如果对面向对象编程感觉不太舒服，你可能会发现<u>python 关于类</u>的文档很有帮助。
- 你可以在<u>python 关于集合</u>的文档中找到一些常见的集合操作。
+- 如果对面向对象编程感觉不太舒服，你可能会发现[<u>python 关于类</u>](https://docs.python.org/3/tutorial/classes.html)的文档很有帮助。
+- 你可以在[<u>python 关于集合</u>](https://docs.python.org/3/library/stdtypes.html#set)的文档中找到一些常见的集合操作。
 - 在 `Sentence` 类中实现 `known_mines` 和 `known_safes` 时，请考虑：在什么情况下，你确信命题的单元格是安全的？在什么情况下，你确定一个命题的单元格是地雷？
 - `add_knowledge` 做了很多工作，可能是迄今为止你为该项目编写的最长的函数。一步一步地实现此函数的行为可能会有所帮助。
 - 如果愿意，欢迎您向任何类添加新方法，但不应修改任何现有函数的定义或参数。
--- a/4.人工智能/4.3.2知识推理.md
+++ b/4.人工智能/4.3.2知识推理.md
@@ -1,8 +1,8 @@
 # 知识推理

 人类根据现有的知识进行推理并得出结论。表示知识并从中得出结论的概念也被用于人工智能中，在本章中我们将探讨如何实现这种行为。
-::: warning 😱
-# 说好的 AI 呢？怎么感觉越来越偏了？
+
+::: warning <font size=5><strong>说好的 AI 呢？怎么感觉越来越偏了？</strong></font>

 如果有这样的疑问的同学，可能存在一定的误区，认为人工智能就是局限在深度学习的算法或者说机器学习的部分算法上，其实这是对这个领域一个巨大的误解。

@@ -20,7 +20,8 @@

 较为基础的知识各位可以看以下的内容。
 :::
-# 基础知识
+
+## 基础知识

 - 基于知识的智能主体 (Knowledge-Based Agents)
  - 智能主体通过对内部的知识表征进行操作来推理得出结论。
@@ -33,7 +34,7 @@
 - 陈述句 (Sentence)
  - 陈述句是知识表示语言中关于世界的断言。陈述句是人工智能存储知识并使用它来推断新信息的方式。

-# 命题逻辑(Propositional Logic)
+## 命题逻辑 (Propositional Logic)

 命题逻辑基于命题。命题是关于世界的陈述，可以是真也可以是假，正如上面例子中的句子。

@@ -41,7 +42,7 @@
  - 命题符号通常是用于表示命题的字母$P、Q、R$
 - 逻辑连接词 (Logical Connectives)
  - 逻辑连接词是连接命题符号的逻辑符号，以便以更复杂的方式对世界进行推理。
-  - <strong>Not</strong><strong> </strong><strong>(</strong>$\lnot$<strong>)</strong> 逻辑非: 命题真值的反转。 例如，如果 $P$：“正在下雨”，那么 $¬P$：“没有下雨”。
+  - <strong>Not</strong><strong> </strong><strong>(</strong>$\lnot$<strong>)</strong> 逻辑非：命题真值的反转。例如，如果 $P$：“正在下雨”，那么 $¬P$：“没有下雨”。
    - 真值表用于将所有可能的真值赋值与命题进行比较。该工具将帮助我们更好地理解与不同逻辑连接词相关联的命题的真值。例如，下面是我们的第一个真值表：

    | $P$      | $\lnot P$ |
@@ -67,10 +68,9 @@
  | 1   | 0   | 1         |
  | 1   | 1   | 1         |

-
  - 值得一提的是，Or 有两种类型：同或 Or 和异或 Or。在异或中，如果$P\lor Q$为真，则$P∧Q$为假。也就是说，一个异或要求它只有一个论点为真，而不要求两者都为真。如果$P、Q$或$P∧Q$中的任何一个为真，则包含或为真。在 Or($\lor$) 的情况下，意图是一个包含的 Or。

- <strong>Implication (→)</strong> 逻辑蕴含: 表示“如果$P$，则$Q$的结构。例如，如果$P$：“正在下雨”，$Q$：“我在室内”，则$P→ Q$的意思是“如果下雨，那么我在室内。”在$P$的情况下，意味着$Q$，$P$被称为前件，$Q$ 被称为后件。
+- <strong>Implication (→)</strong> 逻辑蕴含：表示“如果$P$，则$Q$的结构。例如，如果$P$：“正在下雨”，$Q$：“我在室内”，则$P→ Q$的意思是“如果下雨，那么我在室内。”在$P$的情况下，意味着$Q$，$P$被称为前件，$Q$ 被称为后件。

  - 当前件为真时，在后件为真的情况下，整个蕴含逻辑为真（这是有道理的：如果下雨，我在室内，那么“如果下雨，那么我在室内”这句话是真的）。当前件为真时，如果后件为假，则蕴含逻辑为假（如果下雨时我在外面，那么“如果下雨，那么我在室内”这句话是假的）。然而，当前件为假时，无论后件如何，蕴含逻辑总是真的。这有时可能是一个令人困惑的概念。从逻辑上讲，我们不能从蕴含中学到任何东西$(P→ Q)$如果前件 ($P$) 为假。看一下我们的例子，如果没有下雨，这个蕴含逻辑并没有说我是否在室内的问题。我可能是一个室内型的人，即使不下雨也不在外面走，或者我可能是一个室外型的人，不下雨的时候一直在外面。当前件是假的，我们说蕴含逻辑是真的。

@@ -99,7 +99,7 @@
  - 如果 $α ⊨ β$（$α$蕴含推理出 $β$），那么在任何 $α$为真的世界中，$β$也为真。
  - 例如，如果 $α$：“今天是一月的星期二”和 $β$：“今天是星期二”，那么我们知道 $α ⊨ β$。如果确实是一月的星期二，我们也知道这是星期二。蕴含推理不同于逻辑蕴含。逻辑蕴涵是两个命题之间的逻辑连接。另一方面，推理蕴含关系是指如果 $α$中的所有信息都为真，则 $β$中的所有信息都为真。

-# 推理(Inference)
+## 推理 (Inference)

 推理是从原有命题推导出新命题的过程。

@@ -166,11 +166,11 @@ def check_all(knowledge, query, symbols, model):# 如果模型对每个符号都

 - 此外，`check_all` 函数的工作方式是递归的。也就是说，它选择一个命题符号，创建两个模型，其中一个符号为真，另一个为假，然后再次调用自己，现在有两个模型因该命题符号的真值分配不同而不同。该函数将继续这样做，直到所有符号都已在模型中分配了真值，使 `symbol` 符号为空。一旦它为空（由 `if not symbols` 行标识），在函数的每个实例中（其中每个实例都包含不同的模型），函数检查$KB$是否为给定的有效模型。如果$KB$在此模型中为真，函数将检查查询结论是否为真，如前所述。

-# 知识工程(Knowledge Engineering)
+## 知识工程 (Knowledge Engineering)

 知识工程是弄清楚如何在 AI 中表示命题和逻辑的工程。

-## 推理规则(Inference Rules)
+### 推理规则 (Inference Rules)

 - 模型检查不是一种有效的算法，因为它必须在给出答案之前考虑每个可能的模型（提醒：如果在$KB$为真的所有模型（真值分配）下，查询结论$R$为真，则$R$ 也为真）。推理规则允许我们根据现有知识生成新信息，而无需考虑所有可能的模型。
 - 推理规则通常使用将顶部部分（前提）与底部部分（结论）分开的水平条表示。前提是我们有什么知识，结论是根据这个前提可以产生什么知识。
@@ -232,7 +232,7 @@ def check_all(knowledge, query, symbols, model):# 如果模型对每个符号都

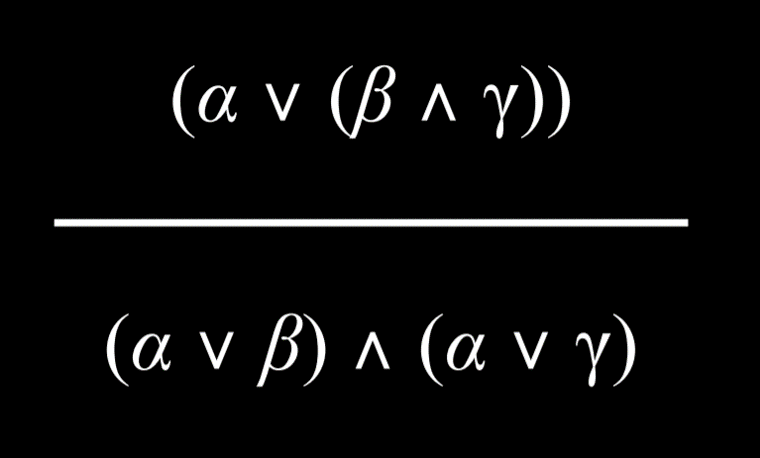
    ![](https://cdn.xyxsw.site/CvPybic63o7jSlxvuzpcFxjQnse.png)

-## 知识和搜索问题
+### 知识和搜索问题

 - 推理可以被视为具有以下属性的搜索问题：

@@ -243,7 +243,7 @@ def check_all(knowledge, query, symbols, model):# 如果模型对每个符号都
  - 路径成本：证明中的步骤数
 - 这显示了搜索算法的通用性，使我们能够使用推理规则根据现有知识推导出新信息。

-# 归结(Resolution)
+## 归结 (Resolution)

 - 归结是一个强大的推理规则，它规定如果 Or 命题中的两个原子命题之一为假，则另一个必须为真。例如，给定命题“Ron 在礼堂”或“Hermione 在图书馆”，除了命题“Ron 不在礼堂”之外，我们还可以得出“Hermione 在图书馆”的结论。更正式地说，我们可以通过以下方式定义归结：

@@ -301,7 +301,7 @@ def check_all(knowledge, query, symbols, model):# 如果模型对每个符号都
    - $(A\lor B)\land\lnot B\vDash A\implies(A ∨ B) ∧ (¬B ∨ C) ∧ (¬C) ∧ (¬A)\land (\lnot B)\land(A)$
    - $(\lnot A\land A)\vDash ()\implies(A ∨ B) ∧ (¬B ∨ C) ∧ (¬C) ∧ (¬A)\land (\lnot B)\land(A)\land ()\implies False$

-# 一阶逻辑(First Order Logic)
+## 一阶逻辑 (First Order Logic)

 - 一阶逻辑是另一种类型的逻辑，它使我们能够比命题逻辑更简洁地表达更复杂的想法。一阶逻辑使用两种类型的符号：常量符号和谓词符号。常量符号表示对象，而谓词符号类似于接受参数并返回 true 或 false 值的关系或函数。
 - 例如，我们回到霍格沃茨不同的人和家庭作业的逻辑谜题。常量符号是指人或房子，如 Minerva、Pomona、Gryffindor、Hufflepuff 等。谓语符号是一些常量符号的真或虚的属性。例如，我们可以使用句子 `person(Minerva)` 来表达 Minerva 是一个人的想法。同样，我们可以用 `house(Gryffindor)` 这个句子来表达 Gryffindor 是一所房子的想法。所有的逻辑连接词都以与以前相同的方式在一阶逻辑中工作。例如，$\lnot$`House(Minerva)` 表达了 Minerva 不是房子的想法。谓词符号也可以接受两个或多个自变量，并表达它们之间的关系。例如，BelongsTo 表达了两个论点之间的关系，即人和人所属的房子。因此，Minerva 拥有 Gryffindor 的想法可以表达为 `BelongsTo(Minerva，Gryffindor)`。一阶逻辑允许每个人一个符号，每个房子一个符号。这比命题逻辑更简洁，因为命题逻辑中每个人的房屋分配都需要不同的符号。
@@ -315,8 +315,8 @@ def check_all(knowledge, query, symbols, model):# 如果模型对每个符号都

 还有其他类型的逻辑，它们之间的共同点是，它们都是为了表示信息而存在的。这些是我们用来在人工智能中表示知识的系统。

-# 补充材料
+## 补充材料

 Introduction to the Theory of Computation, Third International Edition (Michael Sipser)

-具体数学：计算机科学基础.第 2 版
+具体数学：计算机科学基础。第 2 版
--- a/4.人工智能/4.3.3.1程序示例.md
+++ b/4.人工智能/4.3.3.1程序示例.md
@@ -1,11 +1,11 @@
 # 程序示例
+
 ::: tip
 阅读程序，然后“玩一玩”程序！

 完成习题
 :::

-
 ::: tip 📥
 本节附件下载 <Download url="https://cdn.xyxsw.site/code/3-Lecture.zip"/>
 :::
@@ -34,9 +34,7 @@
    8. 0.875
    9. 1
 3. 回答关于贝叶斯网络的问题，问题如下：
-
  ![](https://cdn.xyxsw.site/PUesbhgsFoiucAxWBKYcUUU3nMd.png)
-
  以下哪句话是真的？

    1. 假设我们知道有轨道维护，那么是否有雨并不影响列车准时到达的概率。
--- a/4.人工智能/4.3.3.2项目：遗传.md
+++ b/4.人工智能/4.3.3.2项目：遗传.md
@@ -24,7 +24,7 @@
 ## 理解

 - 打开 `data/family0.csv`，看看数据目录中的一个样本数据集（你可以在文本编辑器中打开，或者在 Google Sheets、Excel 或 Apple Numbers 等电子表格应用程序中打开）。注意，第一行定义了这个 CSV 文件的列：`name`, `mother`, `father`, 和 `trait`。下一行表明 Harry 的母亲是 Lily，父亲是 James，而 `Trait` 的空单元格意味着我们不知道 Harry 是否有这种性状。同时，James 在我们的数据集中没有列出父母（如母亲和父亲的空单元格所示），但确实表现出了性状（如 `Trait` 单元格中的 1 所示）。另一方面，Lily 在数据集中也没有列出父母，但没有表现出这种性状（如 `Trait` 单元格中的 0 表示）。
- 打开 `heredity.py`，首先看一下 `PROBS` 的定义。`PROBS` 是一个包含若干常数的字典，代表各种不同事件的概率。所有这些事件都与一个人拥有多少个特定的突变基因，以及一个人是否基于该基因表现出特定的性状有关。这里的数据松散地基于 GJB2 基因的听力障碍版本和听力障碍性状的概率，但通过改变这些值，你也可以用你的人工智能来推断其他的基因和性状!
+- 打开 `heredity.py`，首先看一下 `PROBS` 的定义。`PROBS` 是一个包含若干常数的字典，代表各种不同事件的概率。所有这些事件都与一个人拥有多少个特定的突变基因，以及一个人是否基于该基因表现出特定的性状有关。这里的数据松散地基于 GJB2 基因的听力障碍版本和听力障碍性状的概率，但通过改变这些值，你也可以用你的人工智能来推断其他的基因和性状！
 - 首先，`PROBS["gene"]` 代表了该基因的无条件概率分布（即如果我们对该人的父母一无所知的概率）。根据分布代码中的数据，在人群中，有 1% 的机会拥有该基因的 2 个副本，3% 的机会拥有该基因的 1 个副本，96% 的机会拥有该基因的零副本。
 - 接下来，`PROBS["trait"]` 表示一个人表现出某种性状（如听力障碍）的条件概率。这实际上是三个不同的概率分布：基因的每个可能值都有一个。因此，`PROBS["trait"][2]` 是一个人在有两个突变基因的情况下具有该特征的概率分布：在这种情况下，他们有 65% 的机会表现出该特征，而有 35% 的机会不表现出该特征。同时，如果一个人有 0 个变异基因，他们有 1% 的机会表现出该性状，99% 的机会不表现出该性状。
 - 最后，`PROBS["mutation"]` 是一个基因从作为相关基因突变为不是该基因的概率，反之亦然。例如，如果一个母亲有两个变异基因，并因此将其中一个传给她的孩子，就有 1% 的机会突变为不再是变异基因。相反，如果一个母亲没有任何变异基因，因此没有把变异基因传给她的孩子，但仍有 1% 的机会突变为变异基因。因此，即使父母双方都没有变异基因，他们的孩子也可能有 1 个甚至 2 个变异基因。
@@ -76,7 +76,7 @@
 ## 一个联合概率例子

 - 为了帮助你思考如何计算联合概率，我们在下面附上一个例子。
- 请考虑以下 `people` 的值:
+- 请考虑以下 `people` 的值：

 ```python
 {
@@ -91,7 +91,7 @@
 - 接下来，我们考虑 James。James 有 2 个变异基因，概率为 `0.01`（这是 `PROBS["gene"][2]`）。鉴于他有 2 个变异基因，他确实具有该性状的概率为 `0.65`。因此，他有 2 个变异基因并且他确实具有该性状的概率是 `0.01*0.65=0.0065`。
 - 最后，我们考虑 Harry。Harry 有 1 个变异基因的概率是多少？有两种情况可以发生。要么他从母亲那里得到这个基因，而不是从父亲那里，要么他从父亲那里得到这个基因，而不是从母亲那里。他的母亲 Lily 没有变异基因，所以 Harry 会以 `0.01` 的概率从他母亲那里得到这个基因（这是 `PROBS["mutation"]`），因为从他母亲那里得到这个基因的唯一途径是基因突变；相反，Harry 不会从他母亲那里得到这个基因，概率是 `0.99`。他的父亲 James 有 2 个变异基因，所以 Harry 会以 `0.99` 的概率从他父亲那里得到这个基因（这是 `1-PROBS["mutation"]`），但会以 `0.01` 的概率从他母亲那里得到这个基因（突变的概率）。这两种情况加在一起可以得到 `0.99*0.99+0.01*0.01=0.9802`，即 Harry 有 1 个变异基因的概率。
 - 考虑到 Harry 有 1 个变异基因，他没有该性状的概率是 `0.44`（这是 `PROBS["trait"][1][false]`）。因此，哈利有 1 个变异基因而没有该性状的概率是 `0.9802 * 0.44 = 0.431288`。
- 因此，整个联合概率是三个人中每个人的所有这些数值相乘的结果: `0.9504 * 0.0065 * 0.431288 = 0.0026643247488`。
+- 因此，整个联合概率是三个人中每个人的所有这些数值相乘的结果：`0.9504 * 0.0065 * 0.431288 = 0.0026643247488`。

 ## 提示

--- a/4.人工智能/4.3.3不确定性问题.md
+++ b/4.人工智能/4.3.3不确定性问题.md
@@ -107,8 +107,8 @@ $P(Flight=取消)=0.1$
 | C=$\lnot$云 | 0.02 | 0.58         |

 - 现在我们可以知道有关这些事件同时发生的信息了。例如，我们知道某一天早上有云，下午有雨的概率是 0.08。早上没有云，下午没有雨的概率是 0.58。
- 使用联合概率，我们可以推导出条件概率。例如，如果我们感兴趣的是在下午下雨的情况下，早上云层的概率分布。$P(C|雨)=\frac{P(C，雨)}{P(雨)}$旁注：在概率上，逗号和$∧$可以互换使用。因此，$P(C,雨)=P(C\land 雨)$。换句话说，我们将降雨和云层的联合概率除以降雨的概率。
- 在最后一个方程中，可以将$P(雨)$视为$P(C,雨)$乘以的某个常数$\alpha=\frac{1}{P(雨)}$。因此，我们可以重写$P(C|雨)=\frac{P(C,雨)}{P(雨)}=αP(C,雨)$，或$α<0.08,0.02>=<0.8,0.2>$。考虑到下午有雨，将$α$分解后，我们可以得到 C 的可能值的概率比例。也就是说，如果下午有雨，那么早上有云和早上没有云的概率的比例是$0.08:0.02$。请注意，0.08 和 0.02 的总和不等于 1；然而，由于这是随机变量 C 的概率分布，我们知道它们应该加起来为 1。因此，我们需要通过算$α$来归一化这些值，使得$α0.08+α0.02=1$。最后，我们可以说$P(C|雨)=<0.8,0.2>$。
+- 使用联合概率，我们可以推导出条件概率。例如，如果我们感兴趣的是在下午下雨的情况下，早上云层的概率分布。$P(C|雨)=\frac{P(C，雨)}{P(雨)}$旁注：在概率上，逗号和$∧$可以互换使用。因此，$P(C，雨)=P(C\land 雨)$。换句话说，我们将降雨和云层的联合概率除以降雨的概率。
+- 在最后一个方程中，可以将$P(雨)$视为$P(C，雨)$乘以的某个常数$\alpha=\frac{1}{P(雨)}$。因此，我们可以重写$P(C|雨)=\frac{P(C，雨)}{P(雨)}=αP(C，雨)$，或$α<0.08,0.02>=<0.8,0.2>$。考虑到下午有雨，将$α$分解后，我们可以得到 C 的可能值的概率比例。也就是说，如果下午有雨，那么早上有云和早上没有云的概率的比例是$0.08:0.02$。请注意，0.08 和 0.02 的总和不等于 1；然而，由于这是随机变量 C 的概率分布，我们知道它们应该加起来为 1。因此，我们需要通过算$α$来归一化这些值，使得$α0.08+α0.02=1$。最后，我们可以说$P(C|雨)=<0.8,0.2>$。

 ## 概率规则 (Probability Rules)

@@ -119,9 +119,9 @@ $P(Flight=取消)=0.1$

 - 边缘化 (Marginalization)：$P(a)=P(a,b)+P(a,\lnot b)$。这里的观点是，$b$和$\lnot b$是独立的概率。也就是说，$b$和$\lnot b$同时发生的概率为 0。我们也知道$b$和$\lnot b$的总和为 1。因此，当$a$发生时，$b$可以发生也可以不发生。当我们把$a$和$b$发生的概率加上$a$和$\lnot b$的概率时，我们得到的只是$a$ 的概率。
 - 随机变量的边缘化可以用：$P(X=x_i)=\sum_jP(X=x_i,Y=y_j)$表示
- 方程的左侧表示“随机变量$X$具有$x_i$值的概率” 例如，对于我们前面提到的变量C，两个可能的值是早上有云和早上没有云。等式的正确部分是边缘化的概念。$P(X=x_i)$等于$x_i$以及随机变量$Y$的每一个值的所有联合概率之和。例如，$P(C=云)=P(C=云,R=雨)+P(C=云,R=\lnot 雨)=0.08+0.32=0.4$。
+- 方程的左侧表示“随机变量$X$具有$x_i$值的概率”例如，对于我们前面提到的变量 C，两个可能的值是早上有云和早上没有云。等式的正确部分是边缘化的概念。$P(X=x_i)$等于$x_i$以及随机变量$Y$的每一个值的所有联合概率之和。例如，$P(C=云)=P(C=云，R=雨)+P(C=云，R=\lnot 雨)=0.08+0.32=0.4$。

-  - 条件边缘化: $P(a)=P(a|b)P(b)+P(a|\lnot b)P(\lnot b)$。这是一个类似于边缘化的想法。事件$a$发生的概率等于给定$b$的概率乘以$b$的概率，再加上给定$\lnot b$的概率乘以$\lnot b$ 的概率。
+  - 条件边缘化：$P(a)=P(a|b)P(b)+P(a|\lnot b)P(\lnot b)$。这是一个类似于边缘化的想法。事件$a$发生的概率等于给定$b$的概率乘以$b$的概率，再加上给定$\lnot b$的概率乘以$\lnot b$ 的概率。
  - $P(X=x_i)=\sum_jP(X=x_i|Y=y_i)P(Y=y_i)$
  - 在这个公式中，随机变量$X$取$x_i$值概率等于$x_i$以及随机变量$Y$的每个值的联合概率乘以变量$Y$取该值的概率之和。如果我们还记得$P(a|b)=\frac{P(a，b)}{P(b)}$，就可以理解这个公式。如果我们将这个表达式乘以$P(b)$，我们得到$P(a,b)$，从这里开始，我们做的与边缘化相同。

@@ -145,20 +145,16 @@ $P(Flight=取消)=0.1$
 | ---- | ----- | ----- |
 | 0.7  | 0.2   | 0.1   |

-
 - Maintenance 对是否有列车轨道维护进行编码，取值为$\set{yes，no}$。Rain 是 Maintenance 的父节点，这意味着 Maintenance 概率分布受到 Rain 的影响。

-
 | R     | yes | no  |
 | ----- | --- | --- |
 | none  | 0.4 | 0.6 |
 | light | 0.2 | 0.8 |
 | heavy | 0.1 | 0.9 |

-
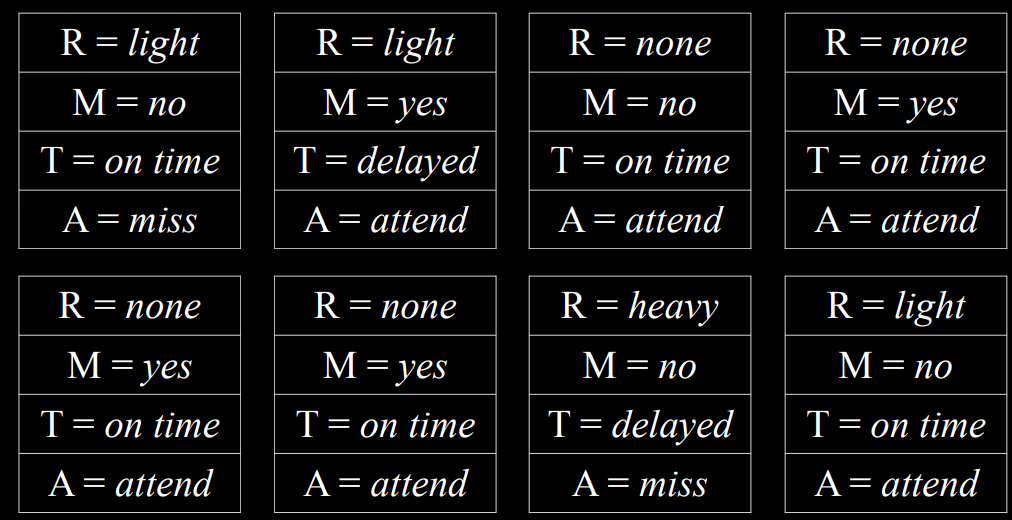
 - Train 是一个变量，用于编码列车是准时还是晚点，取值为$\set{on\ time，delayed}$。请注意，列车上被“Maintenance”和“rain”指向。这意味着两者都是 Train 的父对象，它们的值会影响 Train 的概率分布。

-
 | R      | M   | On time | Delayed |
 | ------ | --- | ------- | ------- |
 | none   | yes | 0.8     | 0.2     |
@@ -168,26 +164,22 @@ $P(Flight=取消)=0.1$
 | heavry | yes | 0.4     | 0.6     |
 | heavy  | no  | 0.5     | 0.5     |

-
 - Appointment 是一个随机变量，表示我们是否参加约会，取值为$\set{attend, miss}$。请注意，它唯一的父级是 Train。关于贝叶斯网络的这一点值得注意：父子只包括直接关系。的确，Maintenance 会影响 Train 是否准时，而 Train 是否准时会影响我们是否赴约。然而，最终，直接影响我们赴约机会的是 Train 是否准时，这就是贝叶斯网络所代表的。例如，如果火车准时到达，可能会有大雨和轨道维护，但这对我们是否赴约没有影响。

-
 | T       | attend | miss |
 | ------- | ------ | ---- |
 | on time | 0.9    | 0.1  |
 | delayed | 0.6    | 0.4  |

-
 - 例如，如果我们想找出在没有维护和小雨的一天火车晚点时错过约会的概率，或者$P(light,no,delayed,miss)$，我们将计算如下：$P(light)P(no|light)P(delayed|light,no)P(miss|delayed)$。每个单独概率的值可以在上面的概率分布中找到，然后将这些值相乘以产生$P(light,no,delayed,miss)$。

-
 ### 推理 (Inference)

 - 在知识推理，我们通过蕴含来看待推理。这意味着我们可以在现有信息的基础上得出新的信息。我们也可以根据概率推断出新的信息。虽然这不能让我们确切地知道新的信息，但它可以让我们计算出一些值的概率分布。推理具有多个属性。
 - Query 查询变量 $X$：我们要计算概率分布的变量。
 - Evidence variables 证据变量$E$: 一个或多个观测到事件$e$ 的变量。例如，我们可能观测到有小雨，这一观测有助于我们计算火车延误的概率。
 - Hidden variables 隐藏变量 $H$: 不是查询结论的变量，也没有被观测到。例如，站在火车站，我们可以观察是否下雨，但我们不知道道路后面的轨道是否有维修。因此，在这种情况下，Maintenance 将是一个隐藏的变量。
- The goal 目标: 计算$P(X|e)$。例如，根据我们知道有小雨的证据 $e$ 计算 Train 变量(查询)的概率分布。
+- The goal 目标：计算$P(X|e)$。例如，根据我们知道有小雨的证据 $e$ 计算 Train 变量 (查询) 的概率分布。
 - 举一个例子。考虑到有小雨和没有轨道维护的证据，我们想计算 Appointment 变量的概率分布。也就是说，我们知道有小雨，没有轨道维护，我们想弄清楚我们参加约会和错过约会的概率是多少，$P(Appointment|light,no)$。从联合概率部分中，我们知道我们可以将约会随机变量的可能值表示为一个比例，将$P(Appointment|light,no)$重写为$αP(Appointment,light,no)$。如果 Appointment 的父节点仅为 Train 变量，而不是 Rain 或 Maintenance，我们如何计算约会的概率分布？在这里，我们将使用边缘化。$P(Appointment,light,no)$的值等于$α[P(Appointment,light,no,delay)+P(Appointment,light,no,on\ time)]$。

 ### 枚举推理
@@ -279,23 +271,25 @@ for node, prediction in zip(model.states, predictions):

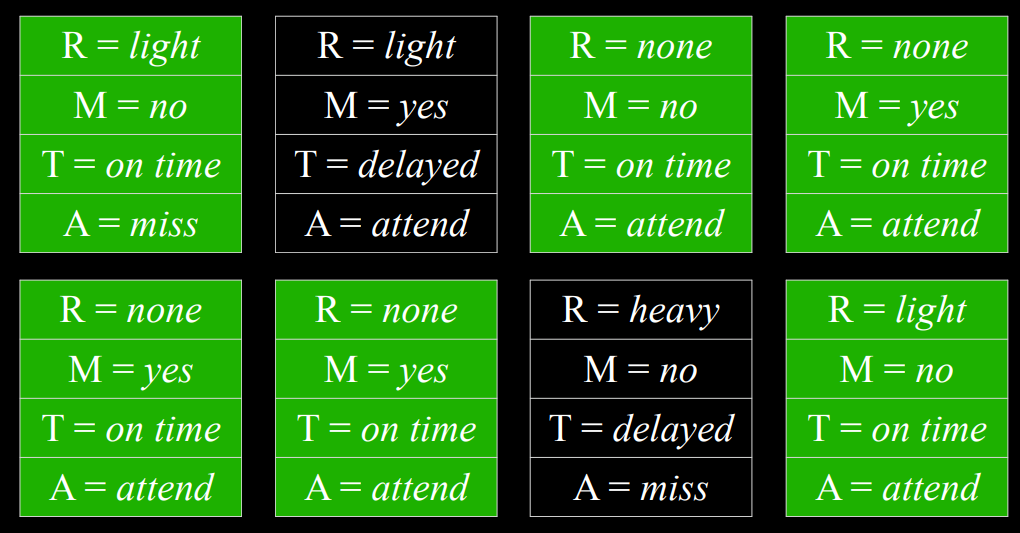
 - 如果我们从对 Rain 变量进行采样开始，则生成的值 none 的概率为 0.7，生成的值 light 的概率为 0.2，而生成的值 heavy 的概率则为 0.1。假设我们的采样值为 none。当我们得到 Maintenance 变量时，我们也会对其进行采样，但只能从 Rain 等于 none 的概率分布中进行采样，因为这是一个已经采样的结果。我们将通过所有节点继续这样做。现在我们有一个样本，多次重复这个过程会生成一个分布。现在，如果我们想回答一个问题，比如什么是$P(Train=on\ time)$，我们可以计算变量 Train 具有准时值的样本数量，并将结果除以样本总数。通过这种方式，我们刚刚生成了$P(Train=on\ {time})$的近似概率。

-![](https://cdn.xyxsw.site/CreObGAg4oXB0oxe2hMcQbYZnAc.png)
-
-![](https://cdn.xyxsw.site/Vr96bdSafoV4kBxJ3x2cAU0TnOg.png)
+<table>
+    <tr>
+        <td><img src=https://cdn.xyxsw.site/CreObGAg4oXB0oxe2hMcQbYZnAc.png width=520></td>
+        <td><img src=https://cdn.xyxsw.site/Vr96bdSafoV4kBxJ3x2cAU0TnOg.png width=520></td>
+    </tr>
+</table>

 - 我们也可以回答涉及条件概率的问题，例如$P(rain=light|train=on\ {time})$。在这种情况下，我们忽略 Train 值为 delay 的所有样本，然后照常进行。我们计算在$Train=\text{on time}$的样本中有多少样本具有变量$Rain=light$，然后除以$Train=\text{on time}$的样本总数。

-![](https://cdn.xyxsw.site/KsELbuMTCoKZkGxU9U5czQpanKg.png)
+<table>
+    <tr>
+        <td><img src=https://cdn.xyxsw.site/KsELbuMTCoKZkGxU9U5czQpanKg.png width=520></td>
+        <td><img src=https://cdn.xyxsw.site/MrP0b2FbXofDsOxgnmncufUynAB.png width=520></td>
+    </tr>
+</table>

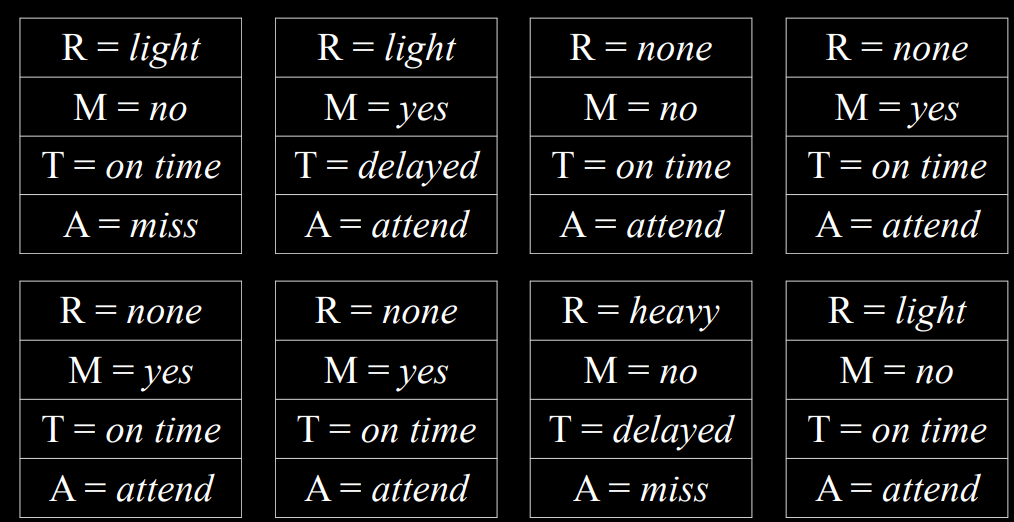
-![](https://cdn.xyxsw.site/MrP0b2FbXofDsOxgnmncufUynAB.png)
-
-去除$T= on time$的样本
-
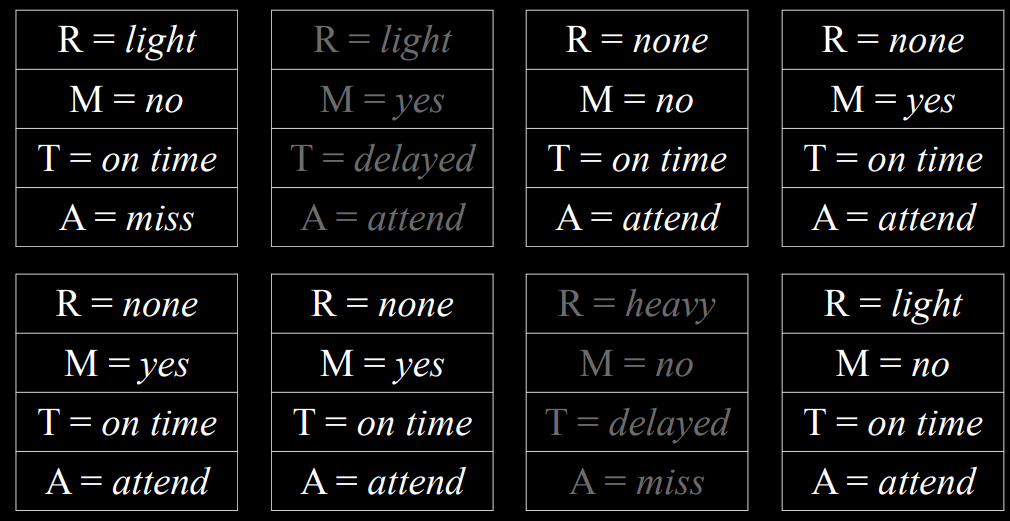
-![](https://cdn.xyxsw.site/Ilj3bPKuwo0l6Dx13rZcVXfenOb.png)
-
-![](https://cdn.xyxsw.site/AptYbb5MZoylvex7LvPcSqivnef.png)
-
-选择$R=light$的样本
+| 去除$T= on time$的样本 | 选择$R=light$的样本 |
+| --------------------- | ------------------ |
+| ![](https://cdn.xyxsw.site/Ilj3bPKuwo0l6Dx13rZcVXfenOb.png) | ![](https://cdn.xyxsw.site/AptYbb5MZoylvex7LvPcSqivnef.png) |

 - 在代码中，采样函数可以是 `generate_sample`：

@@ -341,7 +335,7 @@ print(Counter(data))

  - 首先固定证据变量的值。
  - 使用贝叶斯网络中的条件概率对非证据变量进行采样。
-  - 根据其可能性对每个样本进行加权: 所有证据出现的概率。
+  - 根据其可能性对每个样本进行加权：所有证据出现的概率。
 - 例如，如果我们观察到$Train=\text{on time}$，我们将像之前一样开始采样。我们对给定概率分布的 Rain 值进行采样，然后对 Maintenance 进行采样，但当我们到达 Train 时，我们总是按照观测值取值。然后，我们继续进行，并在给定$Train=\text{on time}$的情况下，根据其概率分布对 Appointment 进行采样。既然这个样本存在，我们就根据观察到的变量在给定其采样父变量的情况下的条件概率对其进行加权。也就是说，如果我们采样了 Rain 并得到了 light，然后我们采样了 Maintenance 并得到了 yes，那么我们将用$P(Train=\text{on time}|light,yes)$来加权这个样本。

 ## 马尔科夫模型 (Markov Models)