chore: turn cos to cdn
This commit is contained in:
@@ -26,7 +26,7 @@
|
||||
|
||||
甚至深度学习,也只是机器学习的一部分,不过使用了更多技巧和方法,增大了计算能力罢了。
|
||||
|
||||

|
||||

|
||||
|
||||
# 两种机器学习算法
|
||||
|
||||
@@ -42,11 +42,11 @@
|
||||
|
||||
近三个月来,每当你的城市里有人卖了房子,你都记录了下面的细节——卧室数量、房屋大小、地段等等。但最重要的是,你写下了最终的成交价:
|
||||
|
||||

|
||||

|
||||
|
||||
然后你让新人根据着你的成交价来估计新的数量
|
||||
|
||||

|
||||

|
||||
|
||||
这就是监督学习,你有一个参照物可以帮你决策。
|
||||
|
||||
@@ -66,7 +66,7 @@
|
||||
|
||||
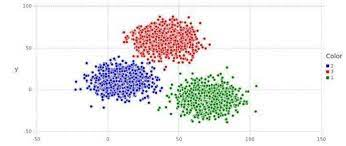
这其实就是一种经典的聚类算法
|
||||
|
||||

|
||||
|
||||
|
||||
可以把特征不一样的数据分开,有非常多的操作,你感兴趣可以选择性的去了解一下。
|
||||
|
||||
@@ -139,7 +139,7 @@ def estimate_house_sales_price(num_of_bedrooms, sqft, neighborhood):
|
||||
|
||||
第二步把每个数值都带入进行运算。
|
||||
|
||||

|
||||

|
||||
|
||||
比如说,如果第一套房产实际成交价为 25 万美元,你的函数估价为 17.8 万美元,这一套房产你就差了 7.2 万。
|
||||
|
||||
@@ -168,13 +168,13 @@ def estimate_house_sales_price(num_of_bedrooms, sqft, neighborhood):
|
||||
|
||||
为了避免这种情况,数学家们找到了很多种[聪明的办法](https://link.zhihu.com/?target=http%3A//en.wikipedia.org/wiki/Gradient_descent)来快速找到优秀的权重值。下面是一种:
|
||||
|
||||

|
||||

|
||||
|
||||
这就是被称为 loss 函数的东西。
|
||||
|
||||
这是个专业属于,你可以选择性忽略他,我们将它改写一下
|
||||
|
||||

|
||||

|
||||
|
||||
<em>θ 表示当前的权重值。 J(θ) 表示「当前权重的代价」。</em>
|
||||
|
||||
@@ -182,7 +182,7 @@ def estimate_house_sales_price(num_of_bedrooms, sqft, neighborhood):
|
||||
|
||||
如果我们为这个等式中所有卧室数和面积的可能权重值作图的话,我们会得到类似下图的图表:
|
||||
|
||||

|
||||

|
||||
|
||||
因此,我们需要做的只是调整我们的权重,使得我们在图上朝着最低点「走下坡路」。如果我们不断微调权重,一直向最低点移动,那么我们最终不用尝试太多权重就可以到达那里。
|
||||
|
||||
@@ -194,7 +194,7 @@ def estimate_house_sales_price(num_of_bedrooms, sqft, neighborhood):
|
||||
|
||||
当你使用一个机器学习算法库来解决实际问题时,这些都已经为你准备好了。但清楚背后的原理依然是有用的。
|
||||
|
||||

|
||||

|
||||
|
||||
枚举法
|
||||
|
||||
@@ -225,7 +225,7 @@ def estimate_house_sales_price(num_of_bedrooms, sqft, neighborhood):
|
||||
|
||||
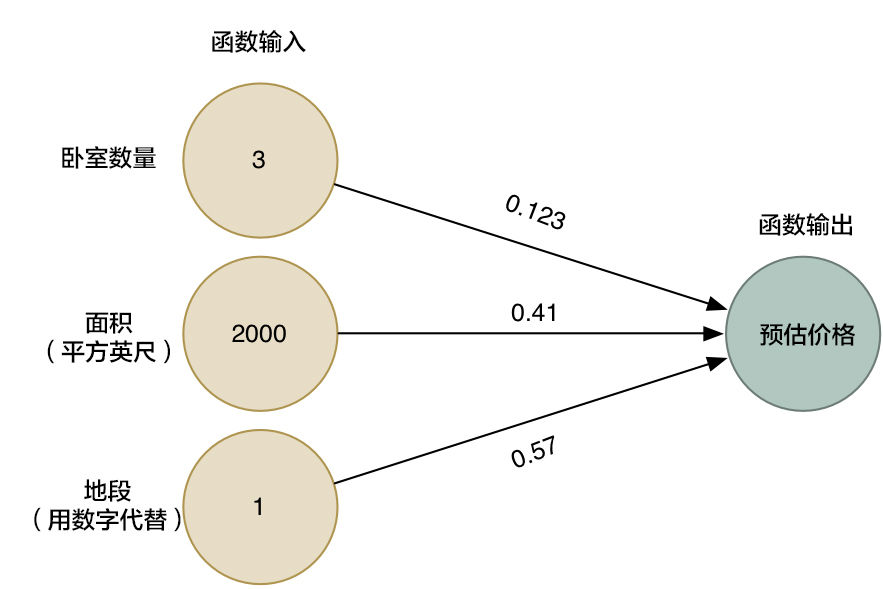
我们换一个好看的形式给他展示
|
||||
|
||||

|
||||
|
||||
|
||||
<em>箭头头表示了函数中的权重。</em>
|
||||
|
||||
@@ -233,17 +233,17 @@ def estimate_house_sales_price(num_of_bedrooms, sqft, neighborhood):
|
||||
|
||||
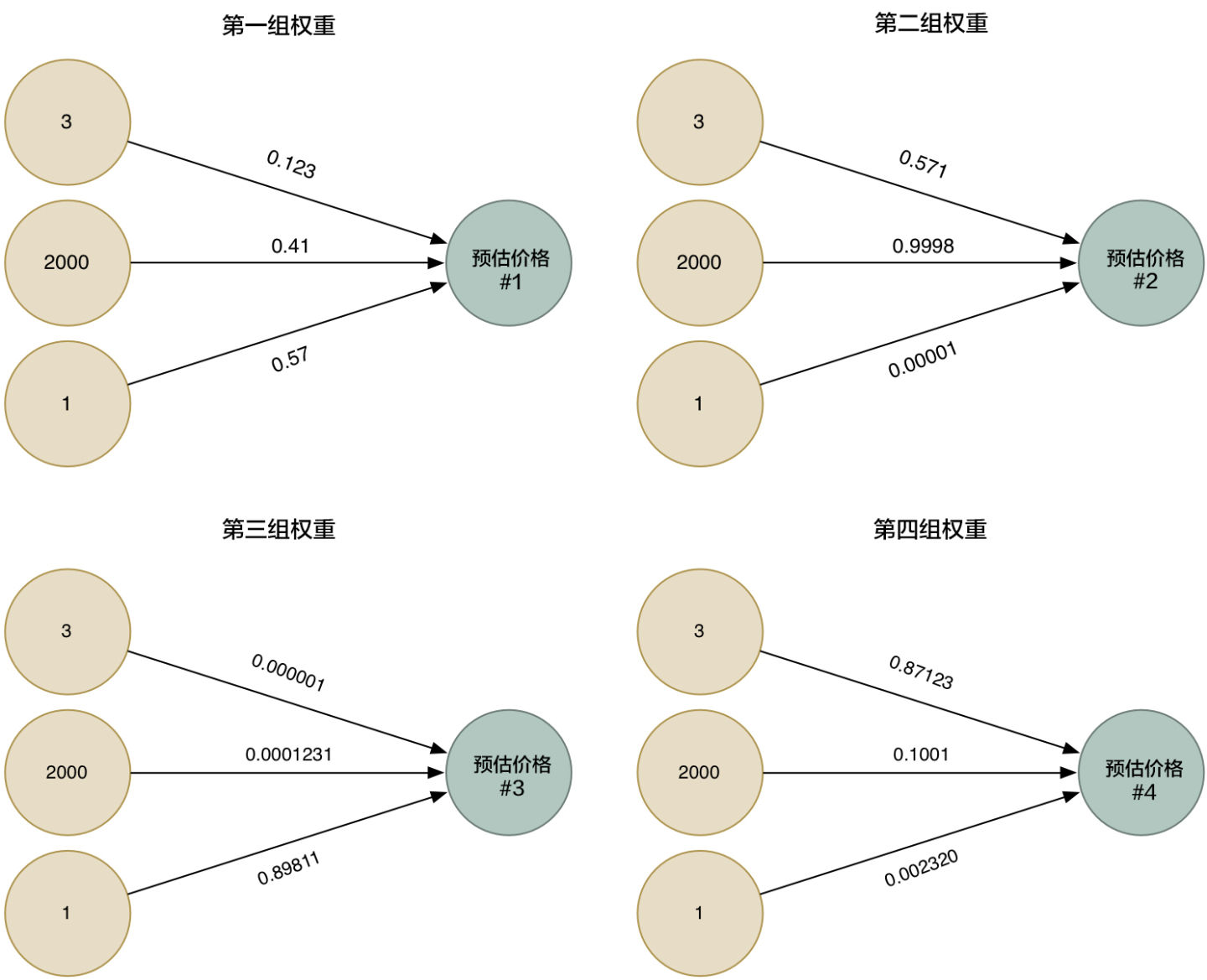
所以为了更加的智能化,我们可以利用不同的权重来多次运行这个算法,收集各种不同情况下的估价。
|
||||
|
||||

|
||||
|
||||
|
||||
然后我们把四种整合到一起,就得到一个超级答案
|
||||
|
||||

|
||||

|
||||
|
||||
这样我们相当于得到了更为准确的答案
|
||||
|
||||
# 神经网络是什么
|
||||
|
||||

|
||||

|
||||
|
||||
我们把四个超级网络的结合图整体画出来,其实这就是个超级简单的神经网络,虽然我们省略了很多的内容,但是他仍然有了一定的拟合能力
|
||||
|
||||
@@ -318,17 +318,17 @@ print('y_pred=',y_test.data)
|
||||
|
||||
我们试着只识别一个数字 8
|
||||
|
||||

|
||||

|
||||
|
||||

|
||||

|
||||
|
||||
我们把一幅 18×18 像素的图片当成一串含有 324 个数字的数组,就可以把它输入到我们的神经网络里面了:
|
||||
|
||||

|
||||

|
||||
|
||||
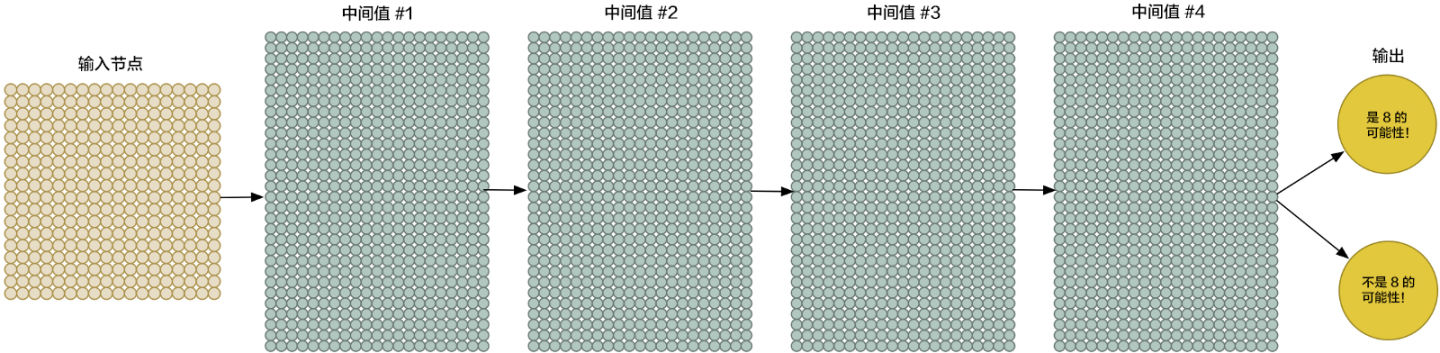
为了更好地操控我们的输入数据,我们把神经网络的输入节点扩大到 324 个:
|
||||
|
||||

|
||||

|
||||
|
||||
请注意,我们的神经网络现在有了两个输出(而不仅仅是一个房子的价格)。第一个输出会预测图片是「8」的概率,而第二个则输出不是「8」的概率。概括地说,我们就可以依靠多种不同的输出,利用神经网络把要识别的物品进行分组。
|
||||
|
||||
@@ -349,7 +349,7 @@ model.add(Activation('relu'))# 激活函数,你可以理解为加上这个东
|
||||
|
||||
当数字并不是正好在图片中央的时候,我们的识别器就完全不工作了。一点点的位移我们的识别器就掀桌子不干了
|
||||
|
||||

|
||||

|
||||
|
||||
这是因为我们的网络只学习到了正中央的「8」。它并不知道那些偏离中心的「8」长什么样子。它仅仅知道中间是「8」的图片规律。
|
||||
|
||||
@@ -365,9 +365,9 @@ model.add(Activation('relu'))# 激活函数,你可以理解为加上这个东
|
||||
|
||||
当然,你同时也需要更强的拟合能力和更深的网络。
|
||||
|
||||

|
||||

|
||||
|
||||

|
||||
|
||||
|
||||
一层一层堆叠起来,这种方法很早就出现了。
|
||||
|
||||
@@ -377,7 +377,7 @@ model.add(Activation('relu'))# 激活函数,你可以理解为加上这个东
|
||||
|
||||
作为人类,你能够直观地感知到图片中存在某种层级(hierarchy)或者是概念结构(conceptual structure)。比如说,你在看
|
||||
|
||||

|
||||

|
||||
|
||||
你会快速的辨认出一匹马,一个人。
|
||||
|
||||
@@ -387,7 +387,7 @@ model.add(Activation('relu'))# 激活函数,你可以理解为加上这个东
|
||||
|
||||
有人对此做过研究,人的眼睛可能会逐步判断一个物体的信息,比如说你看到一张图片,你会先看颜色,然后看纹理然后再看整体,那么我们需要一种操作来模拟这个过程,我们管这种操作叫卷积操作。
|
||||
|
||||

|
||||

|
||||
|
||||
## 卷积是如何工作的
|
||||
|
||||
@@ -395,13 +395,13 @@ model.add(Activation('relu'))# 激活函数,你可以理解为加上这个东
|
||||
|
||||
当然也有最新研究说卷积不具备平移不变性,但是我这里使用这个概念是为了大伙更好的理解,举个例子:你将 8 无论放在左上角还是左下角都改变不了他是 8 的事实
|
||||
|
||||

|
||||

|
||||
|
||||
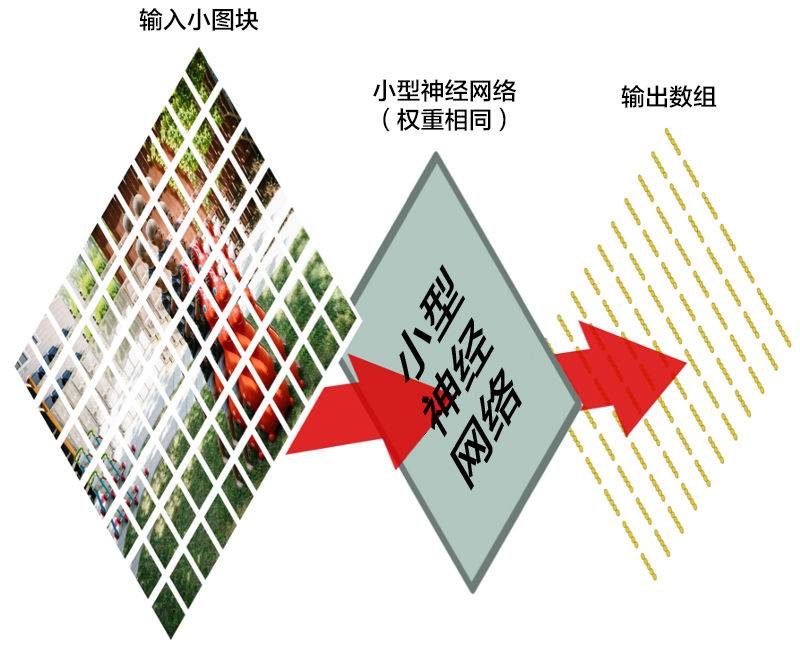
我们将一张图像分成这么多个小块,然后输入神经网络中的是一个小块。<em>每次判断一张小图块。</em>
|
||||
|
||||
然而,有一个非常重要的不同:对于每个小图块,我们会使用同样的神经网络权重。换一句话来说,我们平等对待每一个小图块。如果哪个小图块有任何异常出现,我们就认为这个图块是「异常」
|
||||
|
||||

|
||||
|
||||
|
||||
换一句话来说,我们从一整张图片开始,最后得到一个稍小一点的数组,里面存储着我们图片中的哪一部分有异常。
|
||||
|
||||
@@ -413,7 +413,7 @@ model.add(Activation('relu'))# 激活函数,你可以理解为加上这个东
|
||||
|
||||
让我们先来看每个 2×2 的方阵数组,并且留下最大的数:
|
||||
|
||||

|
||||

|
||||
|
||||
每一波我们只保留一个数,这样就大大减少了图片的计算量了。
|
||||
|
||||
@@ -435,7 +435,7 @@ model.add(Activation('relu'))# 激活函数,你可以理解为加上这个东
|
||||
|
||||
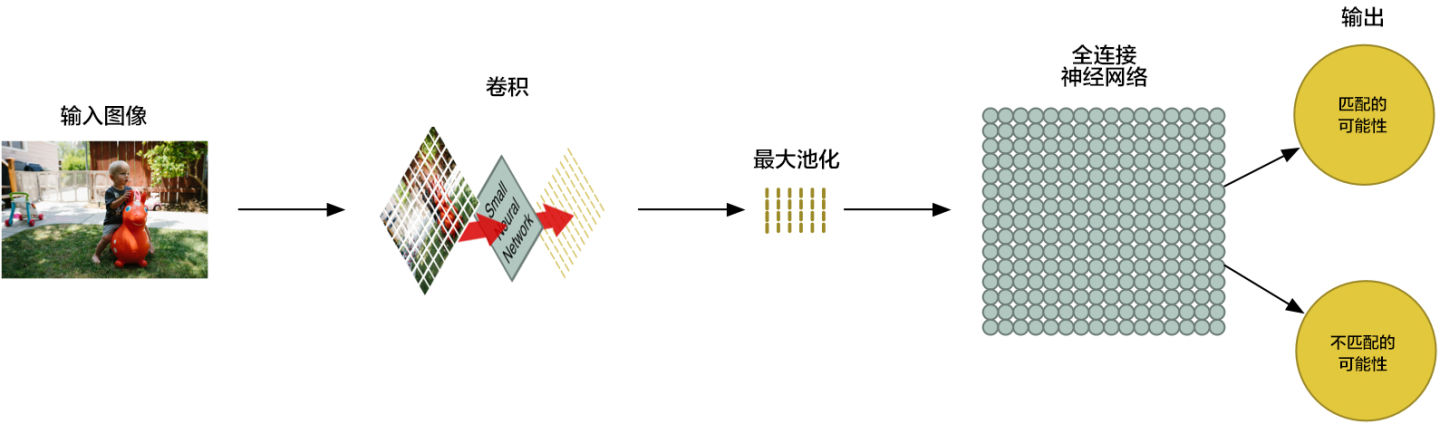
你猜怎么着?数组就是一串数字而已,所以我们我们可以把这个数组输入到另外一个神经网络里面去。最后的这个神经网络会决定这个图片是否匹配。为了区分它和卷积的不同,我们把它称作「全连接」网络
|
||||
|
||||

|
||||
|
||||
|
||||
我们的图片处理管道是一系列的步骤:卷积、最大池化,还有最后的「全连接」网络。
|
||||
|
||||
|
||||
Reference in New Issue
Block a user