📃 docs(4.3人工智能导论及机器学习): 新增4.3.4修改部分之前文档排版及内容

4.人工智能/4.3.1搜索.md

@@ -120,9 +120,9 @@
 
 边域从节点 A 初始化开始
 
-a. 取出边域中的节点 A，展开节点 A，将节点 B 添加到边域。
-b. 取出节点 B，展开，添加......
-c. 到达目标节点，停止，返回解决方案
+1. 取出边域中的节点 A，展开节点 A，将节点 B 添加到边域。
+2. 取出节点 B，展开，添加......
+3. 到达目标节点，停止，返回解决方案
 
 ![](https://cdn.xyxsw.site/XmnObIGaUoF4ssxkgzUc4vTUnmf.png)
 
@@ -212,9 +212,9 @@ def remove(self):
 ![](https://cdn.xyxsw.site/SU2DbQeN2oxs5ex3K3NcMaJfnch.png)
 
 - $A^*$搜索
-  
+
   - 作为贪婪最佳优先算法的一种发展，$A^*$搜索不仅考虑了从当前位置到目标的估计成本$h(n)$，还考虑了直到当前位置为止累积的成本$g(n)$。通过组合这两个值，该算法可以更准确地确定解决方案的成本并在旅途中优化其选择。该算法跟踪（到目前为止的路径成本 + 到目标的估计成本，$g(n)+h(n)$），一旦它超过了之前某个选项的估计成本，该算法将放弃当前路径并返回到之前的选项，从而防止自己沿着$h(n)$错误地标记为最佳的却长而低效的路径前进。
-  
+
   - 然而，由于这种算法也依赖于启发式，所以它依赖它所使用的启发式。在某些情况下，它可能比贪婪的最佳第一搜索甚至不知情的算法效率更低。对于最佳的$A^*$搜索，启发式函数$h(n)$应该：
 
     - 可接受，从未高估真实成本。
@@ -232,11 +232,11 @@ def remove(self):
 - 极大极小算法 (Minimax)
 
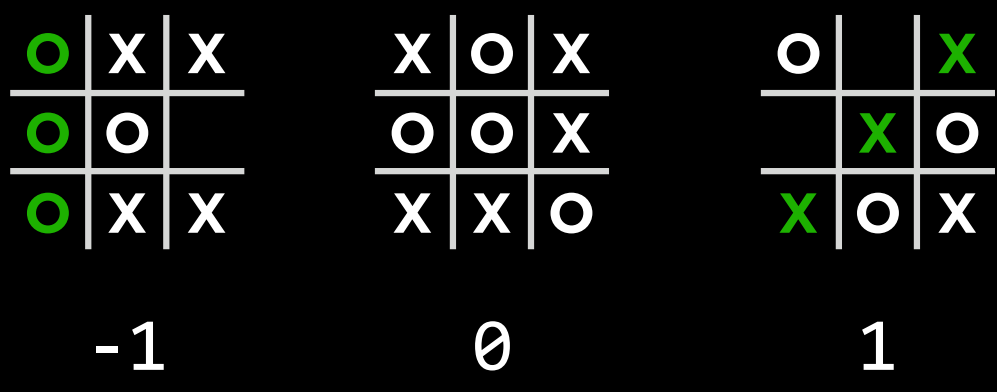
   - 作为对抗性搜索中的一种算法，Minimax 将获胜条件表示为$(-1)$表示为一方，$(+1)$表示为另一方。进一步的行动将受到这些条件的驱动，最小化的一方试图获得最低分数，而最大化的一方则试图获得最高分数。
-  
+
     ![](https://cdn.xyxsw.site/FYu3bQwCZofBgsxKDJiciTR7nzc.png)
-  
+
 - 井字棋 AI 为例
-  
+
   - $s_0$: 初始状态（在我们的情况下，是一个空的 3X3 棋盘）
 
       ![](https://cdn.xyxsw.site/WstnbmHwYoQauRxUQOCclz8Jngb.png)
@@ -285,27 +285,29 @@ def remove(self):
     - 最大化玩家在$Actions(s)$中选择动作$a$，该动作产生$Min-value(Result(s,a))$ 的最高值。
     - 最小化玩家在$Actions(s)$中选择动作$a$，该动作产生$Max-value(Result(s,a))$ 的最小值。
 
-  - Function Max-Value(state):
-    - $$v=-\infty$$
-    - if $Terminal(state)$:
-      - return $Utility(state)$
-    - for $action$ in $Actions(state)$:
-      - $$v = Max(v, Min-Value(Result(state, action)))$$
-    - return $v$
-  - Function Min-Value(state):
-    - $$v=\infty$$
-    - if $Terminal(state)$:
-      - return $Utility(state)$
-    - for $action$ in $Actions(state)$:
-      - $$v = Min(v, Max-Value(Result(state, action)))$$
-    - return $v$
+  ```txt
+  Function Max-Value(state):
+    v=-∞
+    if Terminal(state):
+      return Utility(state)
+    for action in Actions(state):
+      v = Max(v, Min-Value(Result(state, action)))
+    return v
+  Function Min-Value(state):
+    v=+∞
+    if Terminal(state):
+      return Utility(state)
+    for action in Actions(state):
+      v = Min(v, Max-Value(Result(state, action)))
+    return v
+  ```
 
 不会理解递归？也许你需要看看这个：[阶段二：递归操作](../3.%E7%BC%96%E7%A8%8B%E6%80%9D%E7%BB%B4%E4%BD%93%E7%B3%BB%E6%9E%84%E5%BB%BA/3.6.4.2%E9%98%B6%E6%AE%B5%E4%BA%8C%EF%BC%9A%E9%80%92%E5%BD%92%E6%93%8D%E4%BD%9C.md)
 
 - $\alpha$-$\beta$剪枝 (Alpha-Beta Pruning)
 
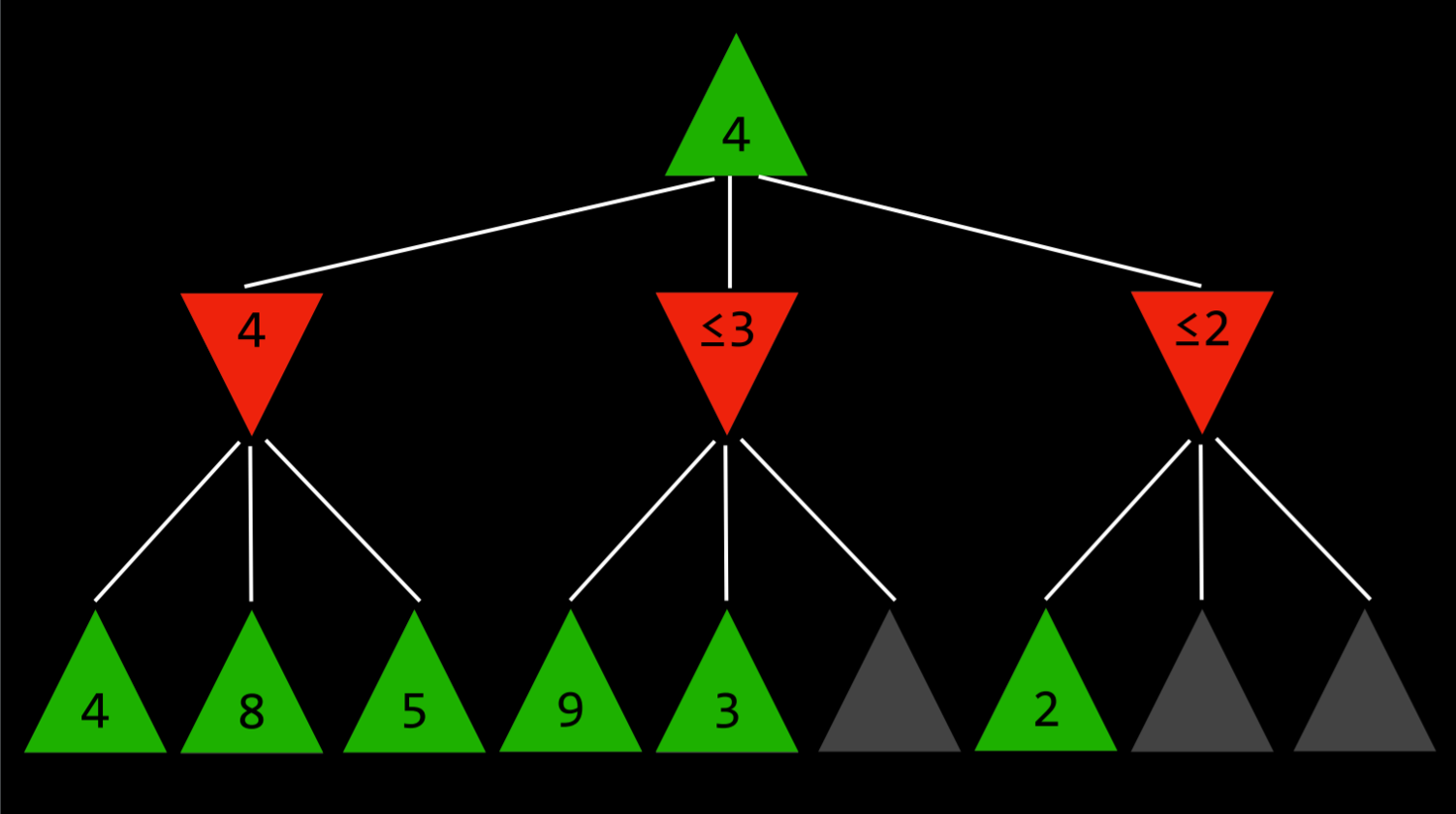
   - 作为一种优化 Minimax 的方法，Alpha-Beta 剪枝跳过了一些明显不利的递归计算。在确定了一个动作的价值后，如果有初步证据表明接下来的动作可以让对手获得比已经确定的动作更好的分数，那么就没有必要进一步调查这个动作，因为它肯定比之前确定的动作不利。
-  
+
   - 这一点最容易用一个例子来说明：最大化的玩家知道，在下一步，最小化的玩家将试图获得最低分数。假设最大化玩家有三个可能的动作，第一个动作的值为 4。然后玩家开始为下一个动作生成值。要做到这一点，如果当前玩家做出这个动作，玩家会生成最小化者动作的值，并且知道最小化者会选择最低的一个。然而，在完成最小化器所有可能动作的计算之前，玩家会看到其中一个选项的值为 3。这意味着没有理由继续探索最小化玩家的其他可能行动。尚未赋值的动作的值无关紧要，无论是 10 还是（-10）。如果该值为 10，则最小化器将选择最低选项 3，该选项已经比预先设定的 4 差。如果尚未估价的行动结果是（-10），那么最小化者将选择（-10）这一选项，这对最大化者来说更加不利。因此，在这一点上为最小化者计算额外的可能动作与最大化者无关，因为最大化玩家已经有了一个明确的更好的选择，其值为 4。
 
 ![](https://cdn.xyxsw.site/LDZab4TeMoByvDxF1Onc8WQenpb.png)